BZOJ3424 : Poi2013 Multidrink
详细做法以及证明请看论文《Hamiltonian paths in the square of a tree》。
首先将1到n的路径提取出来,作为主干。
定义毛毛虫为去掉叶子之后只有一条单链的树,定义non-trivial的毛毛虫为单链非空的毛毛虫。
对于主干上每个点,计算它的非主干部分是否是毛毛虫,如果某个部分不是毛毛虫,那么肯定无解。
将主干上每个点划分为两类:
A:non-trivial的毛毛虫不超过1个。
B:non-trivial的毛毛虫恰有两个。
同时定义一个点是free的当且仅当它是单点。
如下图:
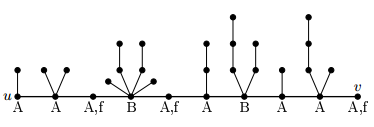
判断一下是否每对相邻的B类点中间都有free点,且所有B类点前后都有free点,如果没有,那么也无解。
现在必然存在一条以1为起点,且依次遍历完主干上每个点及其子树的2H-哈密顿路径。
对于1,如果它是free的,那么方案显然,否则从1出去的点必定是它子树里离它距离只有1的点。
然后一个一个构造,如果上一个点是第二层的点,那么这一部分起点必须为主干上的点,否则起点选第二层的点显然更优。
对于一个毛毛虫,可以直接构造出2H-哈密顿环,从中断开某条路径得到合法的方案。
如下图:

但是如果一个点是B类点,这个时候是不能如此构造的,只能是起点和终点都是第二层的点,而且起点优先考虑叶子节点,这个时候就又可以按之前的方法构造。
最后再检验一下终点是否为n即可,时间复杂度$O(n)$。
#include<cstdio>
#include<cstdlib>
#define N 500010
int n,i,j,x,y,S,T,d[N],g[N],v[N<<1],nxt[N<<1],ed,pre[N],sub[N];
int f[N],G[N],V[N],NXT[N];
int m,a[N],ans,fin[N],cnt,q[N],b[N<<1],tot;bool vip[N],fr[N];
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
void NO(){puts("BRAK");std::exit(0);}
inline void swap(int&a,int&b){int c=a;a=b;b=c;}
inline void reserve(int*a,int n){for(int i=1,j=n;i<j;i++,j--)swap(a[i],a[j]);}
inline void add(int x,int y){d[x]++;v[++ed]=y;nxt[ed]=g[x];g[x]=ed;}
inline void ADD(int x,int y){f[y]=x;V[++ed]=y;NXT[ed]=G[x];G[x]=ed;}
void dfs(int x,int y){
pre[x]=y;
for(int i=g[x];i;i=nxt[i])if(v[i]!=y)dfs(v[i],x);
}
bool spine(int x,int y){
int t=0;
for(int i=g[x];i;i=nxt[i])if(v[i]!=y&&d[v[i]]>1){
if(!spine(v[i],x))return 0;
if(t++)return 0;
}
return 1;
}
inline int any_secondary_node(int x){
for(int i=g[x];i;i=nxt[i])if(!vip[v[i]])return v[i];
}
inline int a_secondary_node_preferably_leaf(int x){
for(int i=g[x];i;i=nxt[i])if(!vip[v[i]]&&d[v[i]]==1)return v[i];
return any_secondary_node(x);
}
inline int another_secondary_node(int x,int y){
for(int i=g[x];i;i=nxt[i])if(!vip[v[i]]&&v[i]!=y)return v[i];
}
void findspine(int x,int y){
q[++cnt]=x;
for(int i=g[x];i;i=nxt[i])if(v[i]!=y)if(d[v[i]]==1)ADD(x,v[i]);else findspine(v[i],x);
}
inline int left(int x){return x==1?tot:x-1;}
inline int right(int x){return x==tot?1:x+1;}
inline void extend(int x,int a=0,int b=0){
for(int i=G[x];i;i=NXT[i])if(V[i]!=a&&V[i]!=b)fin[++ans]=V[i];
}
inline void path_caterpillar(int x,int S,int T){
fin[++ans]=S;
if(S==T)return;
int i,j,A,B;
q[cnt=1]=x;
for(i=g[x];i;i=nxt[i])if(!vip[v[i]]){
if(d[v[i]]==1)ADD(x,v[i]);
else{
if(cnt>1)reserve(q,cnt);
findspine(v[i],x);
}
}
for(i=1;i<=cnt;i++){
b[i]=i&1?q[i]:-q[i];
b[cnt+cnt-i+1]=-b[i];
}
for(tot=0,i=1;i<=cnt+cnt;i++){
if(b[i]<0)if(!G[-b[i]])continue;
b[++tot]=b[i];
}
if(d[S]>1)A=S;else A=-f[S];
if(d[T]>1)B=T;else B=-f[T];
for(i=1;i<=tot;i++)if(b[i]==A)break;
if(A<0)extend(-A,S,T);
if(b[left(i)]==B)
for(j=right(i);b[j]!=B;j=right(j))if(b[j]>0)fin[++ans]=b[j];else extend(-b[j]);
else
for(j=left(i);b[j]!=B;j=left(j))if(b[j]>0)fin[++ans]=b[j];else extend(-b[j]);
if(B<0&&A!=B)extend(-B,S,T);
fin[++ans]=T;
}
int main(){
read(n);
for(i=1;i<n;i++)read(x),read(y),add(x,y),add(y,x);
dfs(n,ed=0);
for(i=1;i!=n;i=pre[i])a[++m]=i;a[++m]=i;
for(i=1;i<=m;i++)vip[a[i]]=1;
for(i=1;i<=m;i++){
x=a[i];fr[x]=1;
for(j=g[x];j;j=nxt[j]){
y=v[j];
if(vip[y])continue;
fr[x]=0;
if(d[y]==1)continue;
sub[x]++;
if(sub[x]>2)NO();
if(!spine(y,x))NO();
}
}
for(i=1,j=0;i<=m;i++){
x=a[i];
if(fr[x])j=1;
else if(sub[x]==2){
if(j!=1)NO();
j=2;
}
}
if(j==2)NO();
S=a[1];
if(fr[a[1]])T=a[1];else T=any_secondary_node(a[1]);
path_caterpillar(a[1],S,T);
for(i=2;i<=m;i++){
x=a[i];
if(fr[x])S=T=x;
else if(!vip[T]){
S=x;
T=a_secondary_node_preferably_leaf(x);
}else{
S=a_secondary_node_preferably_leaf(x);
T=sub[x]<2?x:another_secondary_node(x,S);
}
path_caterpillar(x,S,T);
}
if(fin[n]!=n)NO();
for(i=1;i<=n;i++)printf("%d\n",fin[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号