软件测试 测试路径覆盖
软件测试基础 Graph Coverage 2.3 第七题
7. Use the following method printPrimes() for questions a-f below
1 /******************************************************* 2 * Finds and prints n prime integers 3 * Jeff Offutt, Spring 2003 4 ******************************************************/ 5 public static void printPrimes (int n) 6 { 7 int curPrime; // Value currently considered for primeness 8 int numPrimes; // Number of primes found so far. 9 boolean isPrime; // Is curPrime prime? 10 int [] primes = new int [MAXPRIMES]; // The list of prime numbers. 11 12 // Initialize 2 into the list of primes. 13 primes [0] = 2; 14 numPrimes = 1; 15 curPrime = 2; 16 while (numPrimes < n) 17 { 18 curPrime++; // next number to consider ... 19 isPrime = true; 20 for (int i = 0; i <= numPrimes-1; i++) 21 { // for each previous prime. 22 if (curPrime%primes[i]==0) 23 { // Found a divisor, curPrime is not prime. 24 isPrime = false; 25 break; // out of loop through primes. 26 } 27 } 28 if (isPrime) 29 { // save it! 30 primes[numPrimes] = curPrime; 31 numPrimes++; 32 } 33 } // End while 34 35 // Print all the primes out. 36 for (int i = 0; i <= numPrimes-1; i++) 37 { 38 System.out.println ("Prime: " + primes[i]); 39 } 40 } // end printPrimes
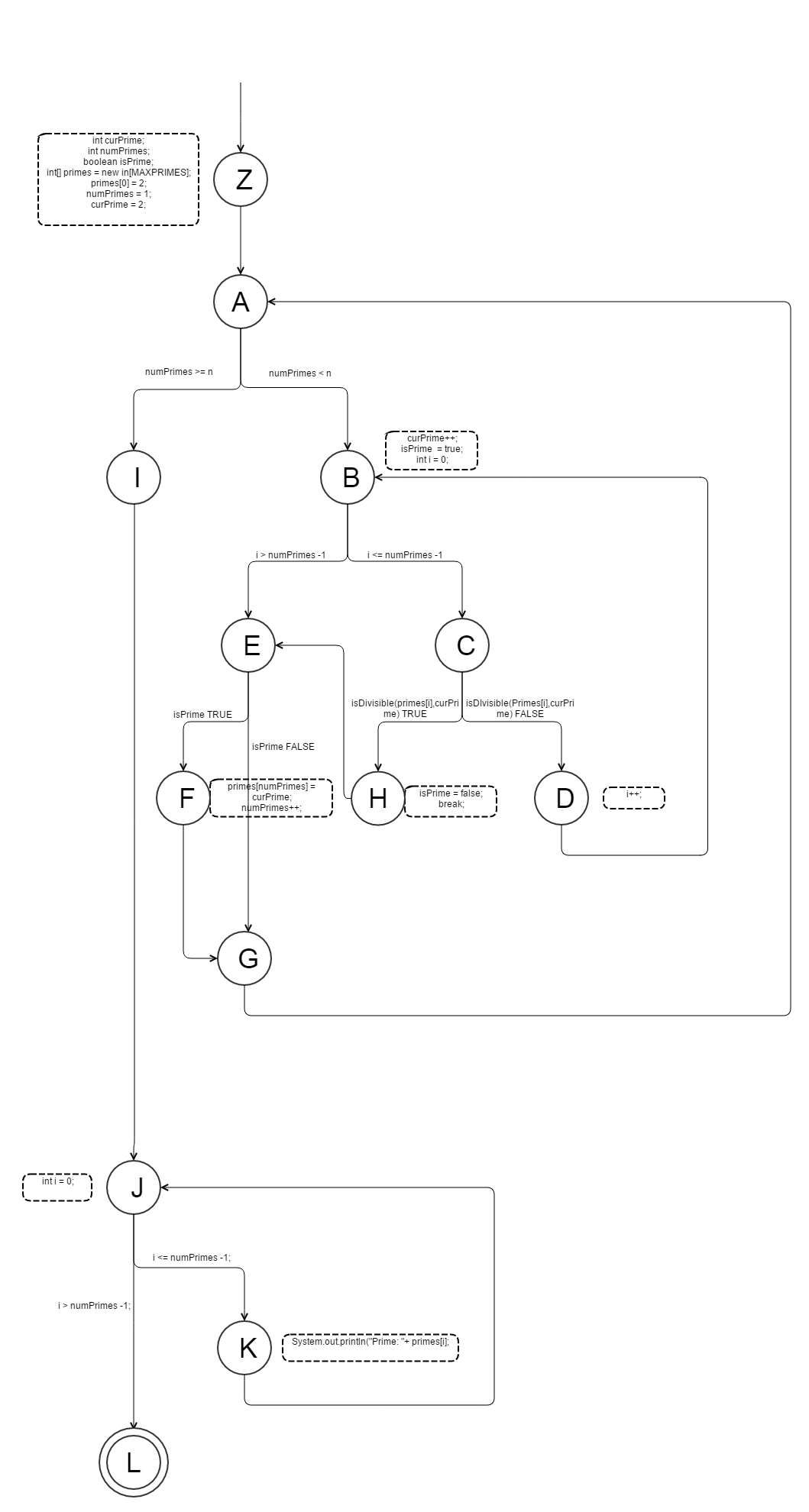
(a) Draw the control flow graph for the printPrimes() method.
(b) Consider test cases t1 = (n = 3) and t2 = (n = 5). Although these tour the same prime paths in printPrimes(), they do not necessarily find the same rime paths in printPrimes(), they do not necessarily find the same faults. Design a simple fault that t2 would be more likely to discover than t1 would.
(c) For printPrimes(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement to the for statement without going through the body of the while loop.
(d) Enumerate the test requirements for nod coverage, edge coverage, and prime path coverage for the graph for printPrimes().
(e) List test paths that achieve node coverage but not edge coverage on the graph.
(f) List test paths that achieve edge coverage but not prime path coverage on the graph.
Answers To:
(a).使用在线作图工具 Gliffy 按要求画出控制流图
(b) 设计一个测试用例t2比t1更有可能找到的错误
只要将数组primes的MAXPRIMES 设置为4, 那么t2 就会比t1 更能找到错误
(c) 不会进入while的内部语句块直接到for循环的测试用例:t3= (n = 1).
(d) TR for
Node coverage: TR= {Z, A, B, C, E, F, G, H, I, J, K, L}
Test path: [Z, A, B, C, D, B, C, H, E, F, G, A, I, J, K, J, ]
Edge coverage: TR= {(Z,A), (A,B), (B,C), (C,D), (C,H), (D,B), (B,E), (H,E), (E,F), (E,G), (F,G), (G,A), (A,I), (I,J), (J,K), (K,J), (J,L)}
Test path: [Z,A,B,C,D,B,C,H,E,G,A,B,C,D,B,E,F,G,A,I,J,K,J,L]
prime path coverage: TR={[Z,A,B,C,D]
[Z,A,B,C,H,E,G]
[Z,A,B,C,H,E,F,G]
[Z,A,B,E,G]
[Z,A,B,E,F,G]
[Z,A,I,J,K]
[Z,A,I,J,L]
[J,K,J]
[K,J,K]
[K,J,L]
[B,C,D,B]
[D,B,C,D]
[A,B,E,G,A]
[A,B,C,H,E,G,A]
[A,B,C,H,E,F,G,A]
[A,B,E,F,G,A]
[G,A,B,E,G]
[G,A,B,C,H,E,G]
[G,A,B,C,H,E,F,G]
[G,A,B,E,F,G]
[D,B,E,G]
[D,B,E,F,G]
[D,B,C,H,E,G]
[D,B,C,H,E,F,G]
[G,A,I,J,L]
[G,A,I,J,K]}
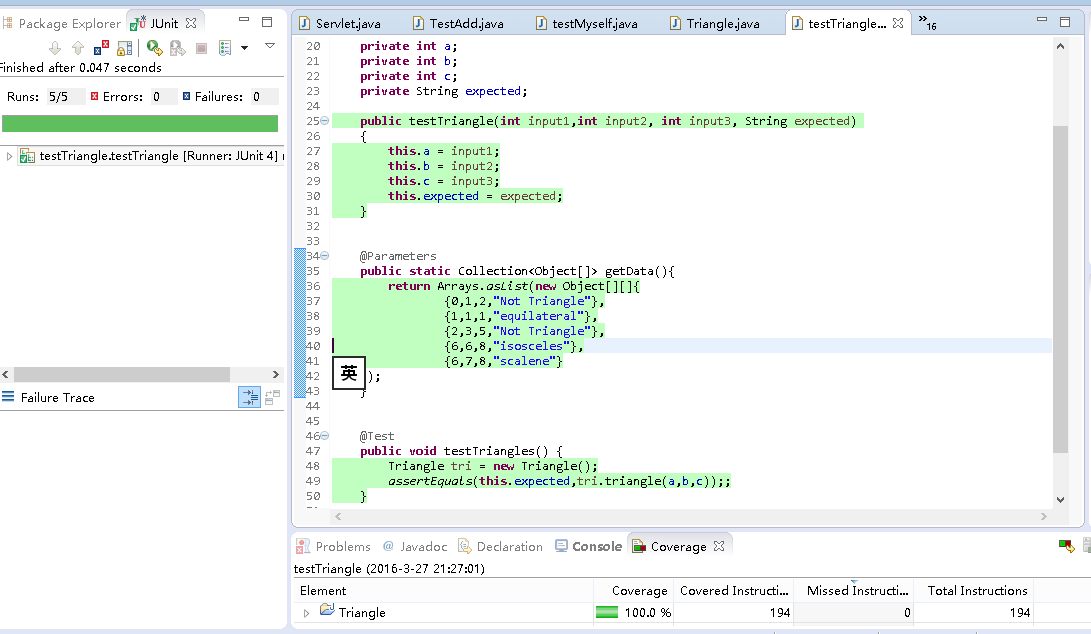
2.基于Junit及Eclemma(jacoco)实现一个主路径覆盖的测试。
使用上次的判断三角形的函数使用
{0,1,2,"Not Triangle"},
{1,1,1,"equilateral"},
{2,3,5,"Not Triangle"},
{6,6,8,"isosceles"},
{6,7,8,"scalene"}
这五个测试用例满足了主路径覆盖