JavaScript统计数据处理(7)- 一维数据生成

在浏览器中运用JavaScript技术处理统计数据具有最佳的推广传播效果
一维数据又称一元数据,是由对等关系的有序或无序信息构成,采用线性方式(一条直线排开)组织在一起。这些数据是平级关系(不是包含、从属关系)。
有序一维数据,使用一维数组表示,如:arr = [3.1 , 3.2 , 4.5];一维数据无序,使用集合类型,如:一维集合st ={ 4.15 , 3.02 , 3.1}。
在JS中,一维数据和多维数据我们都采用JSON数据结构来描述和存储(通过JSON对象转JSON字符),数据处理方法则按根据定义类或对象的形式分类构建。
一维数据生成可以根据序列变化或模拟方法一次性创建一元大样本数据,如正态分布、等差数列等。
导读:
1、数组方法
[返回]ES6提供了新的Array.from()方法可用于各种样本数据的生成,其简单结构样例如下:
console.clear();
let arr = Array.from({length:5}, (v, i) => i);
console.log(arr); // [0, 1, 2, 3, 4]
arr = Array.from({length:5}, (v, i) => 2*i+1);
console.log(arr); // [1, 3, 5, 7, 9]
arr = Array.from({length:5}, (v, i) => Math.random().toFixed(4));
console.log(arr); // ["0.7826", "0.7673", "0.3531", "0.3338", "0.2235"]
注:数组from方法返回参数确定的数组,方法中的length参数为样本生成数量,第二个参数i为数组下标序号
Array.from()方法还有第三个参数,其复合结构样例如下:
console.clear();
let myObj = {
handle: function(n){
return n + 2
}
}
console.log(Array.from(
Array.from({length:5}, (v, i) => i+1), //第一个参数为数组
function (x){return this.handle(x)}, //第二个参数为句柄函数
myObj //第三个参数为句柄函数所指对象(其中包含句柄函数/方法)
)) //[3, 4, 5, 6, 7]
Array.from()方法和Array.map()方法组合运用生成、转换样本,其效果如下:
console.clear();
let arr = Array.from({length:5}, (v, i) => i+1);
arr = arr.map((currentValue,index) => {
return currentValue+2;
})
console.log(arr); //[3, 4, 5, 6, 7]
Array.from()方法和Array.filter()方法组合运用生成、筛选样本,其效果如下:
console.clear();
var arr = Array.from({length:10}, (v, i) => i);
arr = arr.filter((currentValue, index) => {
return currentValue>5;
})
console.log(arr); //[6,7,8,9]
var arr = Array.from({length:100}, (v, i) => i);
arr = arr.filter((currentValue, index) => {
return currentValue%2===0;
})
console.log(arr); //偶数
var arr = Array.from({length:100}, (v, i) => i);
arr = arr.filter((currentValue, index) => {
return currentValue&1===1;
})
console.log(arr); //奇数
2、类的构建
[返回]统计数据处理方法众多,一维数据数量只是比较简单、常用、且非常重要的一类。这里我们首先构造JSON数据对象,JSON对象中大致包括数据处理的基本方法、子对象、属性说明等结构,然后通过object.create()方法建立统计数据分析webData类。
更多关于统计数据分析类的子类、方法、属性等可以逐渐动态添加、封装,类的对象实例可以自动继承这些功能。
console.clear();
var webData = { //统计数据处理对象类
author: "银河统计工作室",
purpose: "JS统计数据分析",
department: "哈尔滨商业大学统计专业",
sayHello: function() {
console.log("来自"+this.department+this.author+"的问候!");
},
xData: { //一维数据处理子类
x:[1,2,3], //样本属性
sum: function(arr) { //求和方法
return arr.reduce((a, b) => a + b);
}
}
}
var myWD = Object.create(webData); //建立对象实例
console.log(myWD.xData.x); //[1,2,3]
console.log(myWD.xData.sum([2,4,7])); //13
webData.xData.author = "Carolyn"; //子类添加属性
webData.xData.purpose = "一维数据分析";
webData.xData.mean = function(arr){ //子类添加求平均数方法
return arr.reduce((a, b) => a + b)/arr.length;
};
webData.xyData = {}; //添加一维数据分析子类
webData.xyData.purpose = "二维数据分析";
//对象实例继承了动态添加的方法
console.log(myWD.xData.mean([2,4,6])); //4
console.log(myWD.xyData.purpose); //二维数据分析
上面代码涉及到JSON结构对象构建webData统计数据处理类、类或子类方法、属性动态添加、引用等。参考这些实例代码,我们可以为一维数据处理子类添加更多方法。
为了简化代码,webData统计数据处理类简化如下:
var webData = {xData:{}}
var myWD = Object.create(webData);
随着数据处理类和方法的统计,webData类的动态添加代码可以整合到一起存储为webData.js基本文件,这些js文件加载到网页中可供不同用户调用。
3、等差数列
[返回]等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。
通项公式为:
\[a_n = a_1+(n-1)\times d\qquad (n=1,2,\cdots)\]式中,\(a_n\)为通项(第n项)、\(a_1\)为初始值、\(d\)为等差。
【等差数列样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {}; //建立数据生成器子类
//==========================================
//等差序列函数:dseq(len, sta=0, step=1)
//函数参数说明:[len:样本数量,sta:初始值,step:等差]
//------------------------------------------
webData.xData.creator.dseq = function(len, sta=0, step=1){
return Array.from({length:len},(v,i)=>step*i+sta);
};
console.log(myWD.xData.creator.dseq(5, 1, 4));
console.log(myWD.xData.creator.dseq(5));
4、等比数列
[返回]等比数列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。这个常数叫做等比数列的公比,公比通常用字母\(q\)表示\((q≠0)\),等比数列第一项\(a1≠0\)。注意,\(q=1\)时,通项\(a_n\)为常数列。
通项公式为:
\[a_n = a_1\times q^{(n-1)}\qquad (n=1,2,\cdots)\]【等比数列样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {};
//==========================================
//等比序列函数:gseq(len, sta=1, step=2)
//函数参数说明:[len:样本数量,sta:初始值,q:等比]
//------------------------------------------
webData.xData.creator.gseq = function(len, sta=1, q=2){
return Array.from({length:len},(v,i)=>sta*Math.pow(q,i));
};
console.log(myWD.xData.creator.gseq(5, 1, 0.5));
console.log(myWD.xData.creator.gseq(5));
5、判别和生成素数
[返回]素数,又称质数,是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
【判别和生成素数代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
//判别一个自然数是否为素数
webData.xData.IS = {}; //建立判别子类
//======================================
//素数判别函数:prime(n)
//函数参数说明:[n:自然数]
//--------------------------------------
webData.xData.IS.prime = function(n){
if (n==1) {return false;}
if (n==2) {return true;}
if (n>2) {
if (n%2===0) {
return false;
} else {
let arr = Array.from({length:n}, (v, i) => i);
arr.splice(0,3);
arr = arr.some((v) => {return n%v===0;})
return !arr;
}
}
};
console.log(myWD.xData.IS.prime(29))
//获得两个有序正整数间的素数
webData.xData.creator = {};
//=======================================
//素数生成函数:getPrime(m, n)
//函数参数说明:[m:下限自然数, n:上限自然数]
//---------------------------------------
webData.xData.creator.getPrime = function(m,n){
let arr = Array.from({length:n}, (v, i) => i+1);
arr.splice(0,m-1);
arr = arr.filter((v) => {return myWD.xData.IS.prime(v);})
return arr;
}
console.log(myWD.xData.creator.getPrime(1,100))
6、斐波那契数列
[返回]斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
通项公式为:
\[F(1)=1,\quad F(2)=1,\quad F(n)=F(n-1)+F(n-2)\qquad (n=3,4,\cdots)\]【斐波那契数列样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {};
//生成n项斐波那契数列
//=======================================
//n项生成函数:fseq1(n)
//函数参数说明:[n:大于2的自然数]
//---------------------------------------
webData.xData.creator.fseq1 = function(n){
let arr = [1,1];
arr = Array.from({length:n-2}, (v, i) => arr[i+2]=arr[i]+arr[i+1]);
arr.unshift(1,1);
return arr
}
console.log(myWD.xData.creator.fseq1(9))
//生成小于v的斐波那契数列项
//=============================
//n项小于v的函数:fseq2(v)
//函数参数说明:[v:大于2的自然数]
//-----------------------------
webData.xData.creator.fseq2 = function(v){
let arr = [1,1];
let i = 1;
while (arr[i]<v) {
i++;
arr[i]=arr[i-2]+arr[i-1];
}
let len = arr.length-1;
if (arr[len]>v) {arr.pop();}
return arr
}
console.log(myWD.xData.creator.fseq2(14))
7、均匀分布样本
[返回]均匀分布(Uniform Distribution)是概率统计中的重要分布之一,均匀分布也叫矩形分布,它在相同长度间隔的分布概率是等可能的。均匀分布由两个参数\(a\)和\(b\)定义,它们是数轴上的最小值和最大值,通常标记为为\(U(a,b)\)。
密度函数:
$$f(x)=\frac{1}{b-a}\qquad(a\le x \le b)$$分布函数:
$$F(x)=\frac{x-a}{b-a}\qquad(a\le x \le b)$$数字特征:
- 期望值:\(E(x)=\frac{a+b}{2}\)
- 方差:\(D(x)=\frac{(b-a)^2}{12}\)
式中,\(a\)为下限值、\(b\)为上限值。
【均匀分布样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {}; //建立数据生成器子类
//=========================================================
//均匀分布函数:random(len, min, max, deci)
//函数参数说明:[len:数量,min:下限值,max:上限值,deci:保留小数]
//---------------------------------------------------------
webData.xData.creator.random = function(len, min=0, max=1, deci=4){
return Array.from({length:len},(v,i)=>
parseFloat(((max-min)*Math.random()+min).toFixed(deci)));
};
//模拟50个U(10,20)均匀分布样本,保留小数4位
console.log(myWD.xData.creator.random(50,10,20));
//模拟50个U(0,1)均匀分布样本,保留小数2位
console.log(myWD.xData.creator.random(50,0,1,2));
//生成模拟掷分币100次样本
console.log(myWD.xData.creator.random(100,0,1,0));
//生成模拟掷色子100次样本
console.log(myWD.xData.creator.random(100,1,6,0));
注:设\(r\)为\((0,1)\)区间的随机数,中JS在,\(r = Math.random()\),在区间\([a,b]\)的均匀分布随机数公式为:\(U=(b-a)\times r+a\)
8、指数分布样本
[返回]指数分布(Exponential distribution)可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。
密度函数和分布图形:
$$f(x)=\lambda{e}^{-\lambda{x}}\qquad{x>0}$$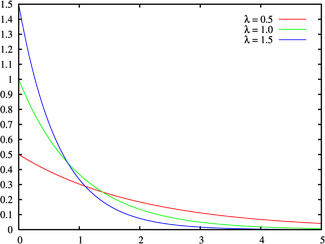
分布函数:
$$F(x)=1-e^{-\lambda{x}}\qquad{x\ge{0}}$$数字特征:
- 期望值:\(E(x)=\frac{1}{\lambda}\)
- 方差:\(D(x)=\frac{1}{\lambda^2}\)
指数分布为连续型随机变量,可通过连续型随机变量密度函数的逆函数产生连续型随机变量样本。逆函数:
$$X=G(r)=-\frac{1}{\lambda}ln(r)$$式中\(X\)服从指数分布、\(r\)为\((0,1)\)区间的随机数、\(\lambda\)为指数分布的率参数(rate parameter),即每单位时间内发生某事件的次数。
【指数分布样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {};
//==============================================
//指数分布:exponential(len, rate, deci)
//参数说明:[len:数量,rate:参数,deci:保留小数]
//----------------------------------------------
webData.xData.creator.exponential = function(len, rate=1, deci=4){
return Array.from({length:len},(v,i)=>
Math.round((-1/rate)*Math.log(Math.random())*Math.pow(10,deci))/Math.pow(10,deci)
)};
console.log(myWD.xData.creator.exponential(10, 0.5));
9、正态分布样本
[返回]正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
密度函数和分布图形:
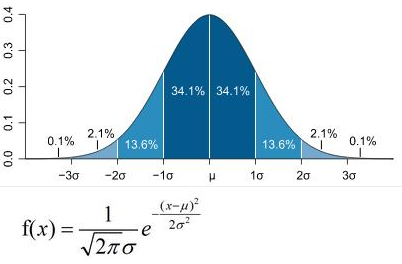
数字特征:
- 期望值:\(E(x)=\mu\)
- 方差:\(D(x)=\sigma\)
正态分布随机样本可以根据均匀分布近似生成。由中心极限定理得知,若n个随机变量\(R_i(1,2,\dots,n)\)独立同分布,当n充分大时\(\sum\limits_{i=1}^n R_i\)趋近于均值为\(n\mu\)、方差为\(n\sigma\)的正态分布随机变量。
若X是n个相互独立的(0,1)区间均匀分布随机变量\(R_i\)的和,则\(R_i\)的均值为\(\frac{1}{2}\)、方差为\(\frac{1}{12}\)。所以X近似于均值为\(\frac{n}{2}\)、方差为\(\frac{n}{12}\)的正态分布随机变量。
若取n=12,则X的均值为6、方差为1。即可认为\(\sum\limits_{i=1}^{12} R_i-6\)近似于标准正态分布随机变量。而随机变量
\[Y=s\times (\sum\limits_{i=1}^{12} R_i-6)+m\]近似于均值为m、标准差为s的正态分布随机变量。
【正态分布样例代码(I)】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {};
//=========================================================
//正态分布:normal(len, mean, std, deci)
//参数说明:[len:数量, mean:均值, std:标准差, deci:保留小数]
//---------------------------------------------------------
webData.xData.creator.normal = function(len, mean=0, std=1, deci=4){
let obj = {
handle: function(v){
return parseFloat((std*(v-6)+mean).toFixed(deci));
}
}
let arr = Array.from(
Array.from({length:len}, (v, x) =>
(Array.from({length:12}, (v, i) =>
Math.random()).reduce((a, b) => a + b))),
function (x){return this.handle(x)},
obj
)
return arr;
}
console.log(webData.xData.creator.normal(1000, 50, 5, 0));
若\(n=12\)不够大,可以取\(n=12\times 9=108\),此时X的均值为54、方差为3。则随机变量
\[Y=\frac{s}{3}\times (\sum\limits_{i=1}^{108} R_i-9\times 6)+m\]服从均值为m、标准差为s的正态分布随机变量。
【正态分布样例代码(II)】
//n = 12*9
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.creator = {};
//=========================================================
//正态分布:normal(len, mean, std, deci)
//参数说明:[len:数量, mean:均值, std:标准差, deci:保留小数]
//---------------------------------------------------------
webData.xData.creator.normal = function(len, mean=0, std=1, deci=4){
let obj = {
handle: function(v){
return parseFloat(((std/3)*(v-6*9)+mean).toFixed(deci));
}
}
let arr = Array.from(
Array.from({length:len}, (v, x) =>
(Array.from({length:12*9}, (v, i) =>
Math.random()).reduce((a, b) => a + b))),
function (x){return this.handle(x)},
obj
)
return arr;
}
console.time('arr');
let arr = webData.xData.creator.normal(100000, 50, 5, 2);
console.log(arr);
console.timeEnd('arr');
10、二项分布样本
[返回]二项分布(Binomial Distribution)即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。
在概率论和统计学中,二项分布是n个独立的“是/非”试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次“成功/失败”试验又称为伯努利试验。实际上,当n = 1时,二项分布就是伯努利分布,二项分布是显著性差异的二项试验的基础。
二项分布在心理与教育研究中,主要用于解决含有机遇性质的问题。所谓机遇问题,即指在实验或调查中,实验结果可能是由 ?猜测而造成的。比如,选择题目的回答,划对划错,可能完全由猜测造成。凡此类问题,欲区分由猜测而造成的结果与真实的结果之间的界限,就要应用二项分布来解决。
密度函数和分布图形:
$$B(k,n,p)=C_{n}^{x}p^{x}(1-p)^{n-x}$$ 其中, $$C_{n}^{x}=\frac{n!}{x!(n-x)!}$$ 式中,x=0、1、2、3、...、n为正整数。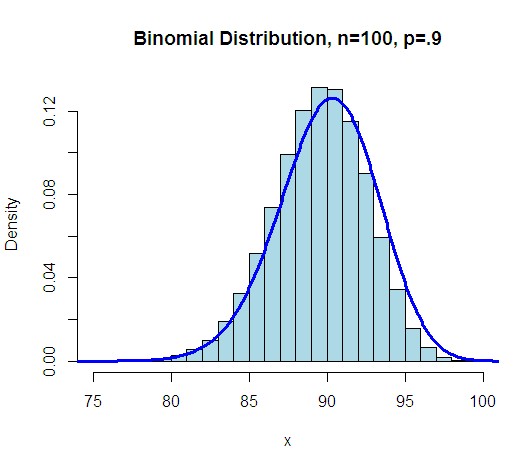
数字特征:
- 期望值:$E(x)=np$
- 方差:$D(x)=\sqrt{np(1-p)}$
二项分布为离散型随机变量,直接抽样方法一般公式为:
$$\sum\limits_{i=0}^{n-1} P_i<r\le \sum\limits_{i=0}^n P_i$$ 式中,确定重复试验次数后产生0-1均匀分布随机数r,满足累计概率条件的r所对应的i即为二项分布样本为随机样本。【案例】:某人射击命中率75%,射击100次。模拟生成100个击中次数随机样本。
解:该问题的击中次数服从二项分布,即
$$P(x=n)=P_n=C_{100}^{n}\times 0.75^{n}\times 0.25^{100-n}$$模拟生成二项分布随机样本计算表如下:
| i-射击次数 | $P_i$-击中概率 | $F_i$-累计概率 | $R_i$-随机数 | $B_i$-二项分布样本 |
|---|---|---|---|---|
| 0 | 6.22E-61 | 6.22E-61 | 0.023365 | 66 |
| 1 | 1.87E-58 | 1.87E-58 | 0.267469 | 72 |
| … | … | … | … | … |
| 81 | 0.036518993 | 0.936988583 | 0.916064 | 81 |
| 82 | 0.025385154 | 0.962373736 | 0.212677 | 72 |
| 83 | 0.016515642 | 0.978889378 | 0.917117 | 81 |
| 84 | 0.010027354 | 0.988916732 | 0.863222 | 80 |
| 85 | 0.005662506 | 0.994579238 | 0.696228 | 77 |
| 86 | 0.002962939 | 0.997542177 | 0.815241 | 79 |
| 87 | 0.001430384 | 0.998972562 | 0.221628 | 72 |
| 88 | 0.00063392 | 0.999606482 | 0.978415 | 83 |
| 89 | 0.000256417 | 0.999862899 | 0.773828 | 78 |
| … | … | … | … | … |
| 100 | 3.21E-13 | 1 | 0.339986368 | 73 |
I、排列(连乘)
【样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData);
webData.xData.calculate = {}; //建立计算子类
//===================
//排列函数:permute(n)
//参数说明:[n:自然数]
//-------------------
webData.xData.calculate.permute = function(n){
let s = 0;
let i;
for (i=1; i<=n; i++) { //先取对数,防止连乘值过大溢出
s += Math.log(i);
}
return Math.round(Math.pow(Math.E,s));
};
console.log(webData.xData.calculate.permute(7)); //5040
II、组合($C_n^m$)
【样例代码】
console.clear();
var webData = {xData:{}}
var myWD = Object.create(webData.xData);
webData.xData.calculate = {};
//===================
//组合函数:combine(n)
//参数说明:[n:自然数, m:自然数]
//-------------------
webData.xData.calculate.combine = function(n,m){
let s1 = 0; let s2 = 0; let i;
for (i=1; i<=m; i++) {s1 += Math.log(i);}
s1 = Math.round(Math.pow(Math.E,s1));
for (i=n-m+1; i<=n; i++) {s2 += Math.log(i);}
s2 = Math.round(Math.pow(Math.E,s2));
return s2/s1;
};
console.log(webData.xData.calculate.combine(7,3)); //35
console.log(myWD.calculate.combine(7,3)); //35
III、二项分布样本
【样例代码】
console.clear();
var webData = {xData:{}}
webData.xData.calculate = {};
webData.xData.calculate.combine = function(n,m){
let s1 = 0; let s2 = 0; let i;
for (i=1; i<=m; i++) {s1 += Math.log(i);}
s1 = Math.round(Math.pow(Math.E,s1));
for (i=n-m+1; i<=n; i++) {s2 += Math.log(i);}
s2 = Math.round(Math.pow(Math.E,s2));
return s2/s1;
};
console.log(webData.xData.calculate.combine(7,3));
webData.xData.creator = {};
//================================
//二项分布:Binomial(n, p)
//参数说明:[n:重复试验次数, p:概率]
//--------------------------------
webData.xData.creator.binomial = function(n,p){
let s = 0;
let arr = Array.from({length:n},(v,i)=>
s += webData.xData.calculate.combine(n,i)*Math.pow(p,i)*Math.pow(1-p,n-i));
let i, v;
let arr1 = [];
for (i=0; i<n; i++) {
v = arr.findIndex((value, index) => {return value>Math.random();});
if (v<0) {v=0;}
arr1.push(v);
}
return arr1;
}
console.log(webData.xData.creator.binomial(100,0.75));
11、泊松分布样本
[返回]泊松分布(Poisson distribution)是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。泊松分布的期望和方差均为λ,参数λ是单位时间(或单位面积)内随机事件的平均发生率。泊松分布适合于描述单位时间内随机事件发生的次数。
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当\(n\ge 10, p\le 0.1\)时,就可以用泊松公式近似得计算。
在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位。
密度函数和分布图形:
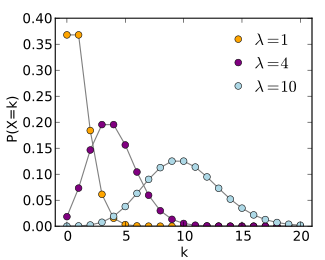
数字特征:
- 期望值:\(E(x)=\lambda\)
- 方差:\(D(x)=\lambda\)
泊松分布为离散型随机变量,直接抽样方法一般公式为:
$$\sum\limits_{i=0}^{n-1} P_i<r\le \sum\limits_{i=0}^n P_i$$式中,确定重复试验次数后产生0-1均匀分布随机数r,满足累计概率条件的r所对应的i即为泊松分布样本为随机样本。
【案例】:试模拟生成100个参数为50(\(\lambda=50\))的泊松分布随机样本。
解:
$$P(x=n)=P_n=e^{-50}\frac{50^n}{n!}$$模拟生成泊松分布随机样本计算表如下:
| i-发生次数 | Pi-发生概率 | sum(Pi)-累计概率 | r-随机数 | 泊松分布 |
|---|---|---|---|---|
| 0 | 1.92875E-22 | 1.92875E-22 | 0.463041 | 49 |
| 1 | 9.64375E-21 | 9.83662E-21 | 0.263746 | 45 |
| … | … | … | … | … |
| 42 | 0.03121317 | 0.143502232 | 0.536319 | 50 |
| 43 | 0.036294383 | 0.179796615 | 0.963988 | 63 |
| 44 | 0.041243617 | 0.221040233 | 0.383948 | 48 |
| 45 | 0.045826241 | 0.266866474 | 0.089723 | 41 |
| 46 | 0.049811132 | 0.316677606 | 0.736878 | 54 |
| … | … | … | … | … |
| 54 | 0.046380787 | 0.742306049 | 0.259084 | 45 |
| 55 | 0.042164352 | 0.784470401 | 0.255274 | 45 |
| … | … | … | … | … |
| 100 | 1.63032E-10 | 1 | 0.462664 | 49 |
【样例代码】
console.clear();
var webData = {xData:{}}
webData.xData.creator = {};
//================================
//泊松分布:Poisson(n, r)
//参数说明:[n:重复试验次数, r:泊松参数]
//--------------------------------
webData.xData.creator.Poisson = function(n, r){
let permute = function permute(n) {
if(n==1 || n==0){return 1;}
return (n*permute(n-1));
}
let prr=Array.from({length:n+1}, (v, i) =>
Math.exp(-r)*Math.pow(r,i)/permute(i));
let brr=[];
let v=prr.reduce(function(a,b) {
brr.push(a+b);
return a+b;
}, 0);
let arr=Array.from({length:n+1}, (v, i) => Math.random());
let i, u;
let xrr=[];
for (i=0; i<=n; i++) {
u = brr.findIndex((currentValue, index) => {
return currentValue>arr[i];
})
xrr.push(u);
}
return xrr;
}
console.log(webData.xData.creator.Poisson(100,50));
12、任意离散分布样本
[返回]任意离散分布指统计与概率学里常见到的离散数据不同状态的比例或比重。在数据处理过程中,将数据按某种标准分类(不同状态,此时分类数据为离散型),统计出每种状态发生次数、进而计算每种状态发生次数所占比重,即为数据的离散分布。由于这种分布不一定属于某种已知分布,故称为“任意分布”。
任何数据都可以通过分类、统计获得其分类状态分布。例如,学习成绩分为优秀、良好、中等、及格和不及格,某班级数学课成绩分布表如下:
| 成绩 | 优秀 | 良好 | 中等 | 及格 | 不及格 | 合计 |
| 比例 | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 | 1.0 |
根据成绩分布模拟生成该班级数学成绩,即所谓任意离散分布样本生成问题。
【案例】:试模拟生成100个上述某班级数学课成绩分布的随机样本。
【样例代码】
console.clear();
var webData = {xData:{}}
webData.xData.creator = {};
//================================
//任意离散分布:RSample(n, arr)
//参数说明:[n:样本数, arr:分布数组, nrr:状态名称数组]
//--------------------------------
webData.xData.creator.RSample = function(n, arr, nrr){
let brr=[];
let v=arr.reduce(function(a,b) {//分布概率累加
brr.push(a+b);
return a+b;
}, 0);
//生成随机数
let crr=Array.from({length:n+1}, (v, i) => Math.random());
let i, u;
let xrr=[];
for (i=0; i<n; i++) {//随机数在累计分布中对应序数
u = brr.findIndex((currentValue, index) => {
return currentValue>crr[i];
})
xrr.push(nrr[u]);
}
return xrr;
}
//输出结果
let oRrr=[0.1,0.2,0.4,0.2,0.1];
let oNrr=["优秀","良好","中等","及格","不及格"];
let oSrr=webData.xData.creator.RSample(100,oRrr,oNrr);
console.log(oSrr);
提示:本页中JS脚本代码可复制粘贴到JS代码运行窗口调试体验; 文本编辑快捷键:Ctrl+A - 全选;Ctrl+C - 复制; Ctrl+X - 剪切;Ctrl+V - 粘贴


 浙公网安备 33010602011771号
浙公网安备 33010602011771号