[吴恩达机器学习笔记]16推荐系统5-6协同过滤算法/低秩矩阵分解/均值归一化
16.推荐系统 Recommender System
觉得有用的话,欢迎一起讨论相互学习~
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
16.5 向量化:低秩矩阵分解Vectorization_ Low Rank Matrix Factorization
示例
- 当给出一件产品时,你能否找到与之相关的其它产品。
- 一位用户最近看上一件产品,有没有其它相关的产品,你可以推荐给他
协同过滤算法
- 我将要做的是:实现一种选择的方法,写出 协同过滤算法 的预测情况
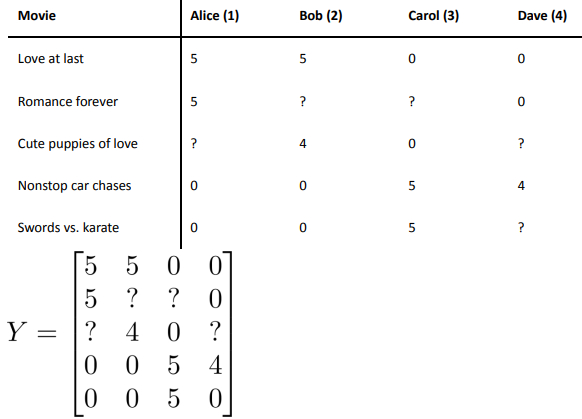
- 我们有关于五部电影的数据集,我将要做的是,将这些用户的电影评分,进行分组并存。我们有五部电影,以及四位用户,那么 这个矩阵 Y 就是一个 5 行 4 列的矩阵,它将这些电影的用户评分数据都存在矩阵里:
![]()
- 使用 协同过滤算法 对参数进行学习,并使用公式\((\theta^{(n_u)})^{T}(x^{(n_m)})\) 对推荐的结果进行预测,得到一个预测值的矩阵,这个矩阵的预测结果和用户评分数据矩阵Y中数据一一对应:
![]()
低秩矩阵分解
- 你也可以将电影的特征按照样本的顺序1,2,3...\(n_m\)按行排列成矩阵X,将用户的特征按照用户的顺序1,2,3...\(n_u\)按行排列成矩阵\(\theta\) 按照\(X\theta^T\)公式进行计算,也可以得到上述 评分预测矩阵 ,这种方法称为 低秩矩阵分解
![]()
电影推荐
- 经过以上操作,我们会学习到电影的一些特征,也许这些特征不是人所能理解的,但是其真的在某种程度上反映了电影的不同特点,例如有的反映了电影的 爱情度 ,动作度 ,喜剧度 等等
- 现在既然你已经对特征参数向量进行了学习,那么我们就会有一个 很方便的方法 来度量两部电影之间的相似性。例如说:电影 i 有一个特征向量 \(x^{(i)}\),你是否能找到一部不同的电影j,保证两部电影的 特征向量之间的距离 \(x^{(i)}\)和 \(x^{(j)}\)很小 ,那就能很有力地表明电影 i 和电影 j在某种程度上有相似,至少在某种意义上,某些人喜欢电影 i,或许更有可能也对电影 j 感兴趣。
\[||x^{(i)}-x^{(j)}||^2
\]
- 当用户在看某部电影 i 的时候,如果你想找 5 部与电影非常相似的电影,为了能给用户推荐 5 部新电影,你需要做的是找出电影 j,在这些不同的电影中与我们要找的电影 i 的距离最小的5部电影,这样你就能给你的用户推荐部不同的可能喜欢电影了。
16.6 推行工作上的细节:均值归一化Implementational Detail_ Mean Normalization
示例引入
- 有一个没有给任何电影评分的用户Eve,加上之前的四个用户,假设电影的特征数为n=2,使用改进的 协同过滤算法(即向量为n维,没有截距项\(\theta_0= 1\)) ,想通过 协同过滤算法 预测Eve用户的偏好特征\(\theta^{(5)}\) ,如下图所示:
![]()
- 由于Eve没有对任何一部电影评过分,所以r(i,j)=1的条件不满足,所以整个式子对\(\theta^{(5)}\)的值有影响的只剩下 正则项
![]()
为了使整个式子最小,则会使正则化项尽可能的为0,所以 \(\theta^{(5)}\)最终的结果是0即\(\theta^{(5)}=\left[\begin{matrix}0\\0\end{matrix}\right]\),这样对于预测Eve用户的偏好特征是没有意义的.所以最后通过\((\theta^{(5)})^{T}x^{(i)}=0\)计算Eve想要看电影的结果也是没有意义的,因为无论\(x^{i}\)的值是何值,结果均为0.
用平均值代替新用户的值
- 如上分析所示,如果新用户在没有对任何电影进行评分的状况下使用协同过滤算法进行预测,最终 得不到任何有意义的结果 ,此时我们想到,对于新用户,我们可以使用每部电影的评分平均值来代替
- 首先需要对结果 Y 矩阵进行均值归一化处理,将每一个用户对某一部电影的评分减去所有 用户对该电影评分的平均值:
![]()
- 然后我们利用这个新的 Y 矩阵来训练算法,如果我们要用新训练出的算法来预测评分,则需要将平均值\(\mu\)重新加回去,即计算$$(\theta{(j)})x^{(i)}+\mu_i$$为最终评分.对于 Eve,虽然\((\theta^{(5)})^{T}x^{(i)}\)仍等于0,但是加上平均值后,我们的新模型会认为她给每部电影的评分都是 该电影的平均分
![]()






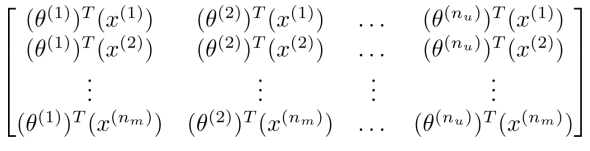


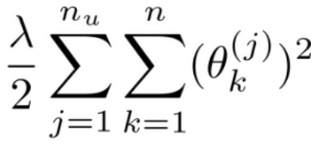
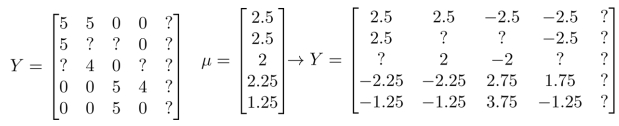


 浙公网安备 33010602011771号
浙公网安备 33010602011771号