[吴恩达机器学习笔记]16推荐系统1-2基于内容的推荐系统
16.推荐系统 Recommender System
觉得有用的话,欢迎一起讨论相互学习~
16.1 问题形式化Problem Formulation
推荐系统的改善能为公司带来巨大的收益
- [以下为Andrew Ng的原话]第一、仅仅因为它是机器学习中的一个重要的应用。在过去几年,我偶尔访问硅谷不同的技术公司,我常和工作在这儿致力于机器学习应用的人们聊天,我常问他们,最重要的机器学习的应用是什么,或者,你最想改进的机器学习应用有哪些。我最常听到的答案是推荐系统。现在,在硅谷有很多团体试图建立很好的推荐系统。因此,如果你考虑网站像亚马逊,或网飞公司或易趣,或 iTunes Genius,有很多的网站或系统试图推荐新产品给用户。如,亚马逊推荐新书给你,网飞公司试图推荐新电影给你,等等。这些推荐系统,根据浏览你过去买过什么书,或过去评价过什么电影来判断。这些系统会带来很大一部分收入,比如为亚马逊和像网飞这样的公司。因此,对推荐系统性能的改善,将对这些企业的有实质性和直接的影响。
- 推荐系统是个有趣的问题,在学术机器学习中因此,我们可以去参加一个学术机器学习会议,推荐系统问题实际上受到很少的关注,或者,至少在学术界它占了很小的份额。但是,如果你看正在发生的事情,许多有能力构建这些系统的科技企业,他们似乎在很多企业中占据很高的优先级。 这是我为什么在这节课讨论它的原因之一。
推荐系统中包含有使机器自动学习特征的思想
- 对机器学习来说,特征是很重要的,你所选择的特征,将对你学习算法的性能有很大的影响。 因此,在机器学习中有一种大思想,它针对一些问题,可能并不是所有的问题,而是一些问题, 有算法可以为你自动学习一套好的特征。 因此,不要试图手动设计,而手写代码这是目前为止我们常干的。有一些设置,你可以有一个算法,仅仅学习其使用的特征,推荐系统就是类型设置的一个例子。还有很多其它的,但是通过推荐系统,我们将领略一小部分特征学习的思想,至少,你将能够了解到这方面的一个例子,我认为,机器学习中的大思想也是这样。因此,让我们开始讨论推荐系统问题形式化。
示例-电影打分
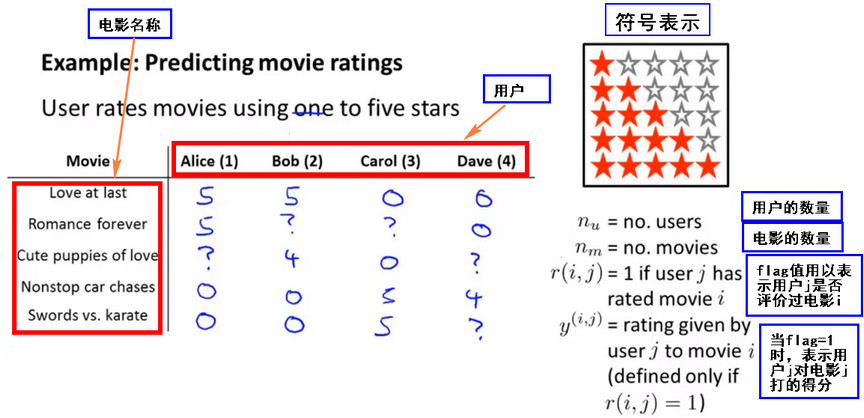
引入标记
- \(n_u\) 代表用户的数量
- \(n_m\) 代表电影的数量
- \(r(i,j)\) 如果用户 i 给电影 j 评过分则 r(i,j)=1
- \(y^{(i,j)}\))代表用户 i 给电影 j 的评分(只在r(i,j)=1时被定义)
- \(m_j\)代表用户 j 评过分的电影的总数
16.2 基于内容的推荐系统Content Based Recommendations
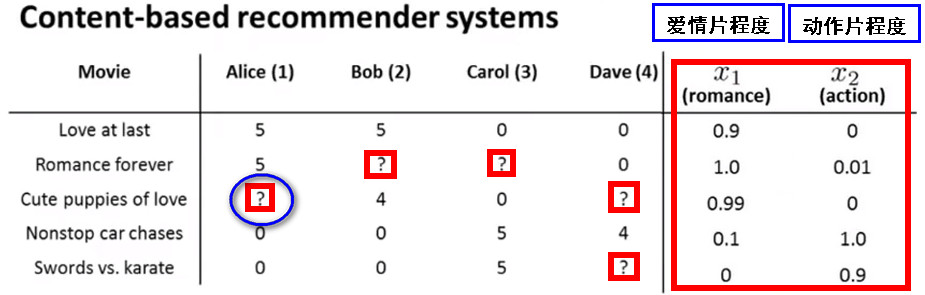
- 假如你有一些用户也有一些电影,每个用户都评价了一些电影,推荐系统要做的就是通过已有的用户评价,预测他们还没有评价过的电影
- 对于没有评价过的电影如何通过已有的评价预测出用户对电影的可能评价(红色框中问号)
-
选定两个为电影的属性 n=2,一个是电影的爱情片程度x1,一个是电影的动作片程度x2,则可以用一个特征向量表示每一部电影(加上截距向量x0=1),则第一部电影可表示为\(x^{(1)}=\left[\begin{matrix}1\\0.9\\0\\\end{matrix}\right]\)
-
![]()
-
使用线性回归构建推荐系统
- 下面我们要基于这些特征来构建一个推荐系统算法。 假设我们采用 线性回归模型 ,我们可以针对 每一个用户 都训练一个线性回归模型,如 \(θ^{(1)}\)是第一个用户的模型的参数。 于是,我们有:
- \(θ^{(j)}\)表示用户 j 的参数向量,考虑到截距项,所以参数维度为(n+1),\(\theta^{(j)}\in R^{3}\),即\(\theta^{(j)}\in R^{n+1}\)
- \(x^{(i)}\)表示电影 i 的特征向量,考虑到截距项,所以参数维度为(n+1),\(x^{(i)}\in R^{3}\),即\(x^{(i)}\in R^{n+1}\)
- 对于用户 j 和电影 i,我们预测评分为:\((θ^{(j)})^Tx^{(i)}\)
- 示例 假设通过学习已经得到\(\theta^{(1)}=\left[\begin{matrix}0\\5\\0\\\end{matrix}\right]\) ,则对于Alice评价Movie《Cute puppies of love》,其值为\((\theta^{(1)})^{T}x^{(3)}=\left[\begin{matrix}0&5&0\end{matrix}\right] * \left[\begin{matrix}1\\0.99\\0\\\end{matrix}\right]=5*0.99=4.95\)
推荐系统线性回归代价函数
- 针对用户 j,该线性回归模型的代价为预测误差的平方和,加上正则化项:
![]()
- 其中 i:r(i,j)表示我们只计算那些用户 j 评过分的电影(即只计算r(i,j)=1的项目)。在一般的线性回归模型中,误差项和正则项应该都是乘以 1/2m,在这里我们将 m 去掉。并且我们不对方差项 \(\theta_0\)(即截距项) 进行正则化处理。 \(y^{(i,j)}表示用户j对电影i的评价的真实值,其中\theta^{(j)}表示用户j的参数,而k表示参数维度的索引\)
- 上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数求和 :
![]()
- 梯度下降公式 计算代价函数的偏导数后得到梯度下降的更新公式如下:其中\(\alpha\)表示学习率,\(\lambda\)表示正则化系数,k=0和k=1时,梯度下降算法是不一样的,因为k=0,\(\theta_0=1\)为定值,梯度为0。
![]()






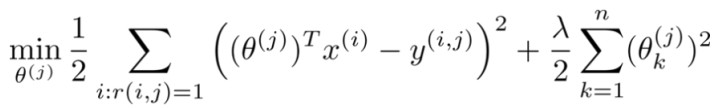
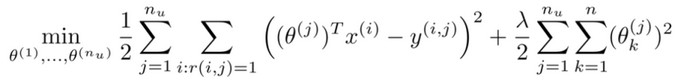
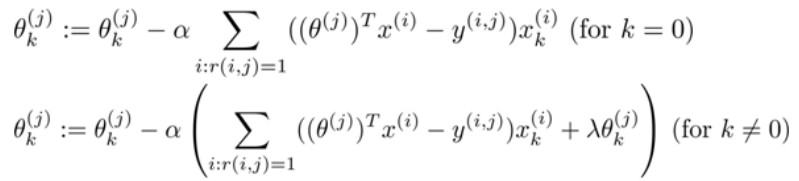

 浙公网安备 33010602011771号
浙公网安备 33010602011771号