[吴恩达机器学习笔记]14降维3-4PCA算法原理
14.降维
觉得有用的话,欢迎一起讨论相互学习~
吴恩达老师课程原地址
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
14.3主成分分析原理Proncipal Component Analysis Problem Formulation
- 主成分分析(PCA)是最常见的降维算法
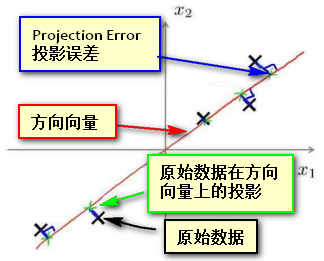
- 当主成分数量K=2时,我们的目的是找到一个低维的投影平面,当把所有的数据都投影到该低维平面上时,希望所有样本 平均投影误差 能尽可能地小。 投影平面 是一个由两个经过原点的向量规划而成的平面,而 投影误差 是 从特征向量向该投影平面作垂线的长度。
- 当主成分数量K=1时,我们的目的是找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,希望所有样本 平均投影误差 能尽可能地小。 方向向量 是一个经过原点的向量,而 投影误差(projection error) 是 从特征向量向该方向向量作垂线的长度。
![]()
- 图中所示为把数据投影到2维空间的情况,图中黑色的×表示原始样本点,红色的是方向向量,蓝色的是投影误差,绿色点表示数据在方向向量上的投影.而 PCA的目的即是希望找到一个方向向量使得所有数据投影在方向向量上的投影误差最小
- Note 在使用PCA之前,需要进行 归一化和特征规范化
主成分分析原理
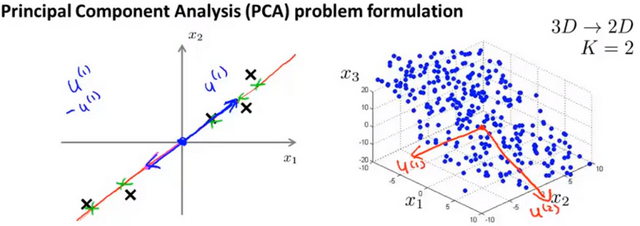
- 从二维降到一维 找到一个能够使数据投影到其上的投影误差最小的方向向量\((\mu^{(1)}\in R^{n})\)。
- 从n维降到k维 找到k个向量\(\mu^{(1)},\mu^{(2)},\mu^{(3)}...\mu^{(k)}\) ,使得原始数据投影到这些向量的线性子空间的投影误差最小。
![]()
PCA和线性回归不一样
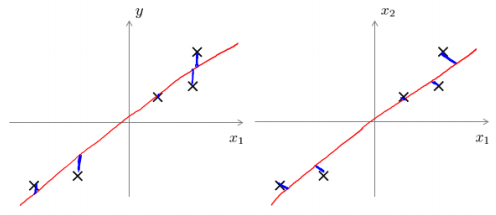
- 从工作机制和得到的结果上看,PCA和线性回归方法很像,看似都是找到一个可以近似拟合原始数据的线或平面 ,尽管看上去很相似但实际上却完全不一样。
- 主成分分析最小化的是投射误差(ProjectedError),而线性回归尝试的是最小化预测误差。 主成分分析 是一种 无监督学习方法 ,线性回归 是一种 监督学习方法 , 线性回归的目的是预测结果,而主成分分析不作任何预测,原始数据的所有特征属性在主成分分析中都是一样对待的。下图中,左边的是线性回归的误差( 垂直于横轴投影 ),右边则是主要成分分析的误差( 垂直于方向向量投影 )。
![]()
PCA的优点与缺点
- 优点
- PCA 技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
- PCA 技术的一个很大的优点是,它是完全无参数限制的。在 PCA 的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
- 缺点
- 这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
14.4主成分分析算法Proncipal Component Analysis algorithm
- 假设使用PCA方法将原始数据集中的N维数据降到K维
- 均值归一化 计算所有特征的均值\(\mu_j\),然后将原始数据中所有维度都减去该维度的 均值\(\mu_j\) ,即令\(x_j=x_j-\mu_j\),如果特征在不同的数量级上,还需要将其除以该维度自身的 标准差\(\sigma^{2}\)
- 计算样本集合的 协方差矩阵(covariance matrix) ,每个N维向量维度为(N1),乘以自身维度为(1N)的转置,得到一个(N*N)的对称矩阵,将所有样本矩阵之和相加后即得到样本集合的 协方差矩阵Σ
即: $$Σ=\frac{1}{m}\sum{n}_{i=1}(x)(x{(i)})$$
Note 如果\(x^{(i)}\) 本身是以行向量的方式存储,假设X是样本\(x^{(i)}\)逐层堆叠而成的样本矩阵,则有:$$Σ=\frac{1}{m} * X^{T} * X$$ 即
![]()
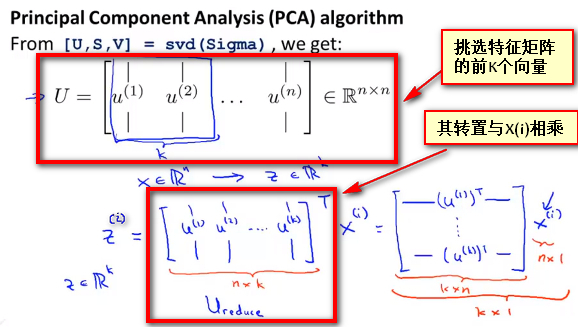
- 计算协方差矩阵Σ的 特征向量(eigenvectors) ,可以使用 奇异值分解(singular value decomposition) 进行求解, 在matlab中使用语句 [U,S,V]=svd(sigma) ,其中sigma表示Σ即样本集合的协方差矩阵,
![]()
上式的U是一个具有与数据之间最小投射误差的方向向量构成的矩阵 。如果我们希望 将数据从N维降至K维 ,我们只需要从U中选取前K个向量即上图中的 \(u^{(1)},u^{(2)},u^{(3)},...u^{(K)}\) ,获得一个N×K维度的矩阵,使用\(U_reduce\)表示,然后通过如下计算获得要求的新特征向量\(z^{(i)}\),即有 $$z{(i)}=U_{reduce} * x^{(i)}$$ 其中\(x^{(i)}\)是N * 1维的样本向量, 而\(U^{T}\)是一个K * N维的方向向量构成的矩阵,因此最终结果Z^{(i)}是一个K * 1维的向量 ,即是 通过PCA得到的新的特征向量
![]()
- 总结
![]()






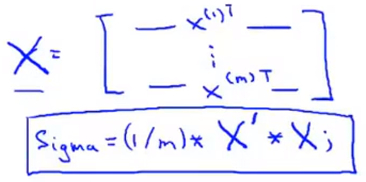
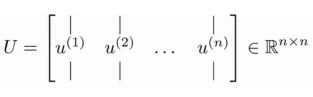


 浙公网安备 33010602011771号
浙公网安备 33010602011771号