[吴恩达机器学习笔记]14降维1-2降维的应用数据压缩与数据可视化
14.降维
觉得有用的话,欢迎一起讨论相互学习~
吴恩达老师课程原地址
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
14.1动机一：数据压缩
- 降维 也是一种无监督学习的方法，降维并不需要使用数据的标签。
- 降维 的其中一个目的是 数据压缩，数据压缩不仅能够压缩数据，使用较少的计算机内存或磁盘空间，更可以加快我们的学习算法。
- 降维 能很好的处理 特征冗余，例如：在做工程时，有几个不同的工程队，也许第一个工程队给你二百个特征，第二工程队给你另外三百个的特征，第三工程队给你五百个特征，一千多个特征都在一起，这些特征中往往都存在着巨大的冗余，而且去跟踪这些大量的特征会变得及其困难。
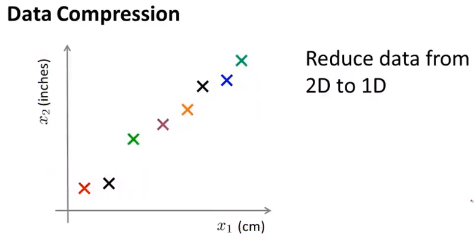
将2维特征降到1维
- 以下举个例子，假如测量某个物品的长度，横轴表示使用厘米作为单位进行测量的结果，纵轴表示使用英尺作为单位进行测量的结果，这两个特征是由大量冗余的 但是由于测量时的四舍五入导致测量结果并不一定相等，因此我们想通过降维的方式 去掉冗余的数据
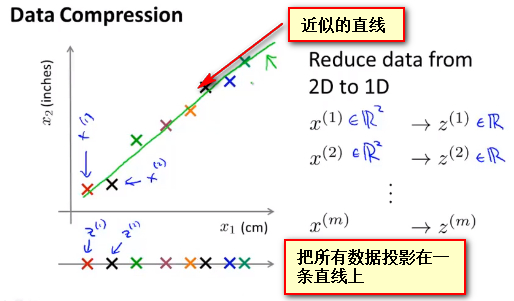
- 此时想找到一条看起来大多数据都落在其旁边的线，而使得所有的数据都能投影在刚才的线上， 通过这种做法，我能够测量出每个样本在线上的位置以建立新特征 \(Z_1\) ,即是原来的数据我需要用\(x_{(1)},x_{(2)}\)两个维度的特征进行表示，而现在只需要通过新特征\(Z\)的一个值就能表示原有的两个特征的内容
- 通过把样本投影在一条近似的直线上，能够通过一个实数值就能表示原有数据集的所有样本 其中\(x^{(1)},x^{(2)},x^{(3)},x^{(4)}...x^{(m)}\) 用以表示数据集中的样本，\(x_1,x_2\)用以表示原始数据集中的特征，\(z^{(i)}\) 用以表示第i个样本通过降维后得到的新特征。
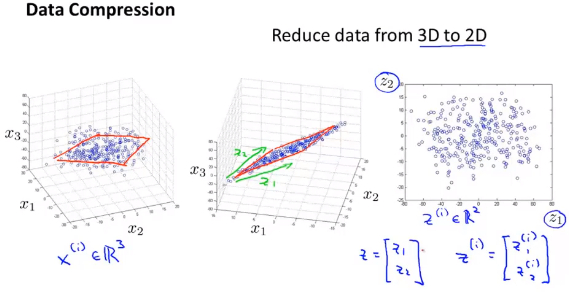
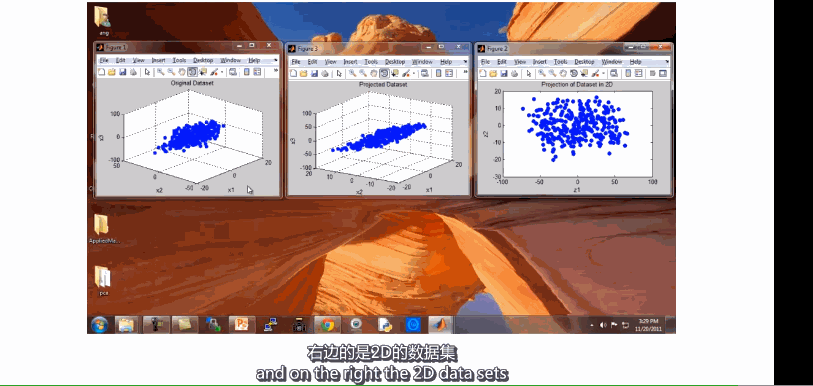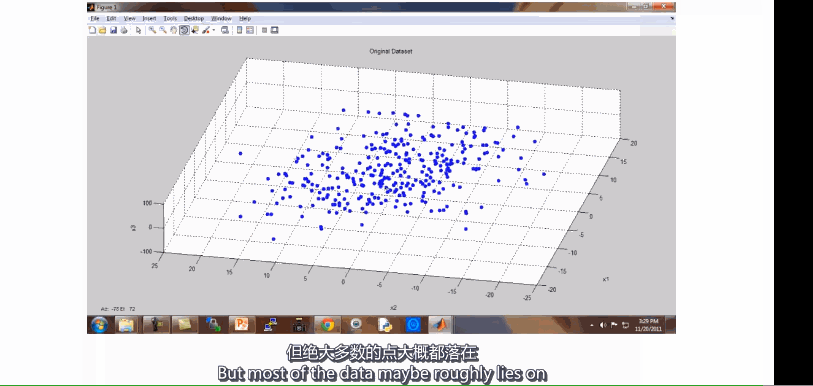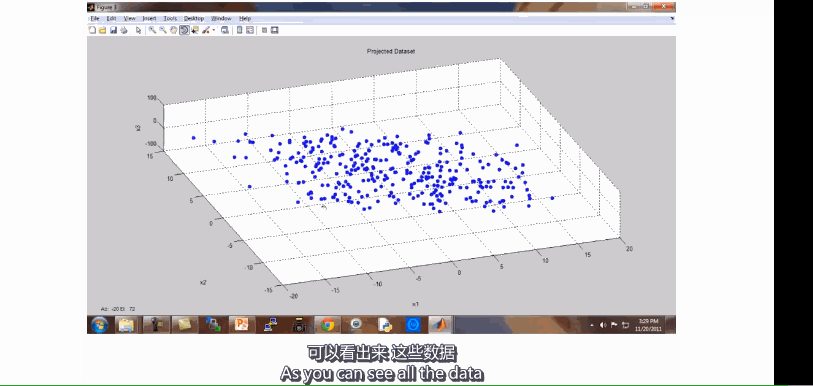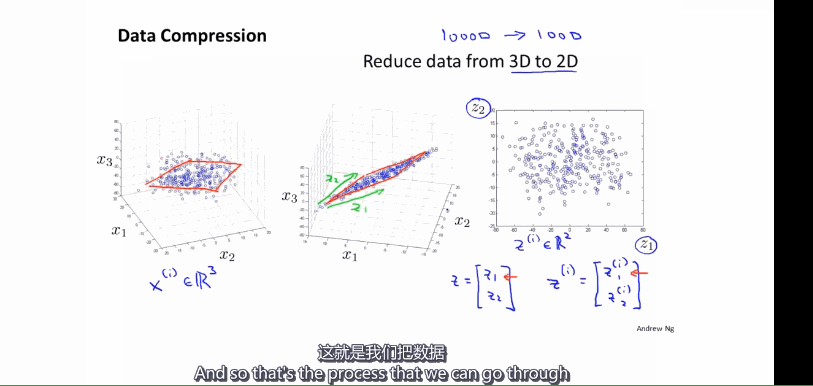
将3维特征降到2维
- 将三维向量投影到一个二维的平面上，迫使所有的数据都在同一个平面上，降至二维的特征向量。原有的三维数据点变成二维的平面，而二维的特征表示数据点在二维平面上的位置。其中原始的三个特征使用\(X_1,X_2,X_3\)表示，新的特征使用\(Z_1,Z_2\)表示，意义是投影平面的两条坐标轴,$z^{(i)}用以表示第i个样本通过降维得到的新特征。
14.2动机二：数据可视化
- 目前我们只能对2-3维的数据进行可视化，一旦数据的维度变得很大，我们将不能很直观的发现数据中的规律。此时， 降维 就成了一个很直观很重要的工作。
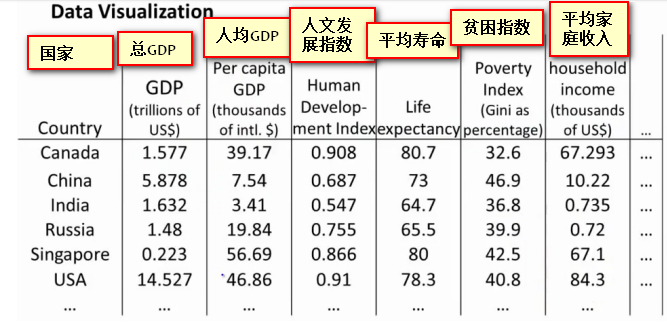
- 如下是国家发展水平的一张报表，通过50个指标对国家进行评估，我们想用可视化的方法进行直观的查看，但是50维的数据是不可能使用图形进行绘制的，为此我们使用降维的方法将其降低到2维进行查看。
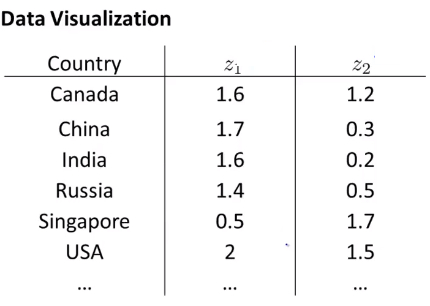
- 通过降维的方法50个维度被整合成两个新的特征\(Z_{1}和Z_{2}\) ,但是我们对于新特征的意义，我们并不清楚。即 降维 只能将数据的维度降低而对于新特征的意义需要重新发现与定义。
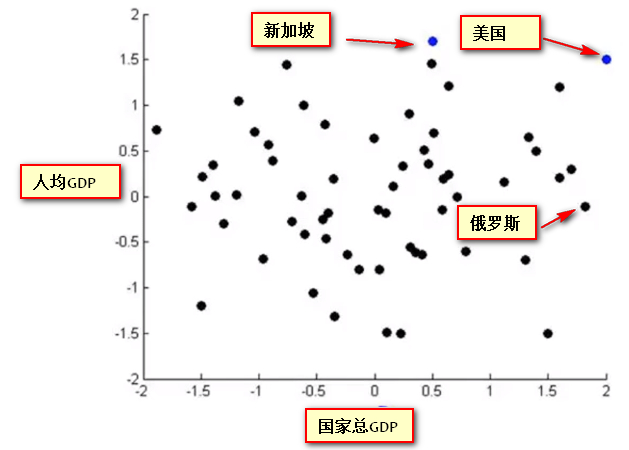
- 使用图形表示降维后的新特征:
- 横轴约表示为国家整体经济强度/国家生产总值GDP
- 纵轴约表示幸福指数/人均生产总值
