[吴恩达机器学习笔记]12支持向量机5SVM参数细节
12.支持向量机
觉得有用的话,欢迎一起讨论相互学习~
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
12.5 SVM参数细节
标记点选取
- 标记点(landmark)如图所示为\(l^{(1)},l^{(2)},l^{(3)}\),设核函数为 高斯函数 ,其中设预测函数y=1 if \(\theta_0+\theta_{1}f_1+\theta_{2}f_2+\theta_{3}f_3\ge0\)
![]()
- 在实际中需要用 很多标记点 ,那么如何选取 标记点(landmark) ,即使用训练集中的样本作为标记点 ,假设有一个样本为 \(x^{(1)}\) ,则在相同的位置可以设置标记点 \(l^{(1)}\) , 此时可以得到m个标记点与训练集中样本数一致,且每一个标记点的位置都与每一个样本的位置一致。 因为这说明特征函数基本上是在描述每一个样本距离与样本集中其他样本的距离
![]()
- 取 样本集(不仅仅是训练集,而是所有样本) 中的样本作为标记点.
![]()
- 然后使用 相似度 函数计算 每个样本和标记点之间的特征\(f_n\) ,并且将所有的 \(f_n\) 集合成 特征向量f .并且将默认的特征(截距)\(f_0\)设为1,如下图所示:
![]()
- 示例 假设训练集中有样本 \(x^{(i)}\) ,则可以通过相似度函数计算出其与各个标记点的特征值从而组成特征向量 \(f^{(i)}\)
![]()
对于第i个标记点,由于有定义\(x^{(i)}=l^{(i)}\),所以有 $$f_i{(i)}=sim(x,l{(i)})=exp(-\frac{0}{2\sigma{2}})=1$$ ,而定义有 截距特征 为1,则有以下结果:
![]()
应用SVM
- 如果已经学到了参数 \(\theta\) ,再给定x的值,并对y做预测,首先要重新计算特征f,并且要满足式子 \("y=1" if\ \theta^{T}f\ge 0\) .其中\(\theta\) 也是一个m+1维的向量,m是训练集的数量
- 此时需要最小化的损失函数如下:
![]()
- 在具体实施过程中,我们还需要对最后的归一化项进行些微调整,在计算\(\sum^{n}_{j=1}\theta^{2}_{j}=\theta^{T}\theta\)时,我们用\(\theta^{T}M\theta\)代替\(\theta^{T}\theta\)其中 M 是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算
- 理论上讲,我们也可以在逻辑回归中使用核函数,但是上面使用 M 来简化计算的方法不适用与逻辑回归,因此计算将非常耗费时间
- 在此,我们不介绍最小化支持向量机的代价函数的方法,你可以使用现有的软件包(如liblinear,libsvm 等)。在使用这些软件包最小化我们的代价函数之前,我们通常需要编写核函数,并且如果我们使用高斯核函数,那么在使用之前进行特征缩放是非常必要的。
- 另外,支持向量机也可以不使用核函数,不使用核函数又称为线性核函数(linear kernel),当我们不采用非常复杂的函数,或者我们的训练集特征非常多而实例非常少的时候,可以采用这种不带核函数的支持向量机
SVM参数
正则化参数C
- 正则化参数C和神经网络正则化参数\(\lambda\)的倒数\(\frac{1}{\lambda}\)类似
- 大的C对应于小的\(\lambda\),这意味着不使用正则化,会得到一个低偏差(bias),高方差(variance)的模型,则会更加倾向于 过拟合
- 小的C对应于大的\(\lambda\),这意味着更多的正则化,会得到一个高偏差(bias),低方差(variance)的模型,则会更加倾向于 欠拟合
高斯核函数\(\sigma^{2}\)
- 如果\(\sigma\)较大时,曲线较为平滑,会下降地更为 平缓 ,会得到一个高偏差(bias),低方差(variance)的模型,则会更加倾向于 欠拟合
- 如果\(\sigma\)较小时,曲线较为陡峭,会下降地更为 迅速 ,会得到一个低偏差(bias),高方差(variance)的模型,则会更加倾向于 过拟合
![]()










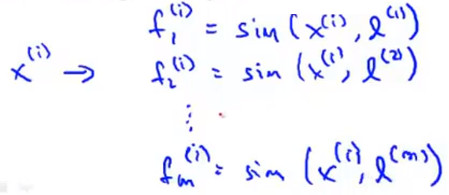

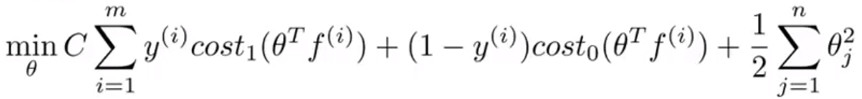


 浙公网安备 33010602011771号
浙公网安备 33010602011771号