[吴恩达机器学习笔记]12支持向量机4核函数和标记点kernels and landmark
12.支持向量机
觉得有用的话,欢迎一起讨论相互学习~
12.4 核函数与标记点- Kernels and landmarks
问题引入
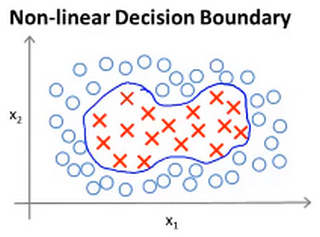
- 如果你有以下的训练集,然后想去拟合其能够分开正负样本的非线性判别边界。
![]()
- 一种办法是构造一个复杂多项式特征的集合:
\[h_{\theta}(x)=\begin{cases}
1\ \ if\ \ \theta_{0}+\theta_{1}x_1+\theta_{2}x_2+\theta_{3}x_1x_2+\theta_{4}x_{1}^{2}+\theta_{5}x_{2}^{2}+...\ge 0\\
0\ \ otherwise\ \
\end{cases}
\]
- 然而类似于\(x_1x_2或x_1^2及x_2^2\)等人为定义的特征是不是最好的呢?我们能不能通过函数来进行学习得到更复杂拟合度更高的特征来解决非线性问题呢?此时我们可以借助于待定系数法,把不同的特征看做是待定的未知的目标进行确定 , 使用\(f_n\)表示待定的目标特征。
- 即新的表达式为:
\[h_{\theta}(x)=\begin{cases}
1\ \ if\ \ \theta_{1}f_1+\theta_{2}f_2+\theta_{3}f_3+\theta_{4}f_4+\theta_{5}f_5+\theta_{6}f_6+...\ge 0\\
0\ \ otherwise\ \
\end{cases}
\]
特征构建
- 假设此处需要构建3个新特征。
- 首先在坐标\(x_1和x_2\)上选取三个 地标(landmark) \(l^{(1)},l^{(2)},l^{(3)}\)
![]()
- 然后给定一个样本x, 定义特征\(f_1\)为样本x和地标\(l^{(1)}\)的相似度
\[f_1=similarity(x,l^{(1)})=exp(-\frac{||x-l^{(1)}||^2}{2\sigma^{2}}) \]- 同样的 定义特征\(f_2\)为样本x和地标\(l^{(2)}\)的相似度
\[f_2=similarity(x,l^{(2)})=exp(-\frac{||x-l^{(2)}||^2}{2\sigma^{2}}) \]- 类似的 定义特征\(f_3\)为样本x和地标\(l^{(3)}\)的相似度
\[f_3=similarity(x,l^{(3)})=exp(-\frac{||x-l^{(3)}||^2}{2\sigma^{2}}) \] - 首先在坐标\(x_1和x_2\)上选取三个 地标(landmark) \(l^{(1)},l^{(2)},l^{(3)}\)
- 此处的 相似度函数 即\(exp(-\frac{||x-l^{(n)}||^2}{2\sigma^{2}})\) 就是所说的 核函数 ,而核函数有很多种,即有很多种不同的定义相似度的方法,此处的核函数被称为 高斯核函数(Gaussian Kernel)
核函数和相似度
- 公式的展开项如下图所示,从图中可以看出
- 当x和landmark十分接近时,特征值为约等于1
- 当x和landmark距离很远时,特征值为约等于0
![]()
高斯核函数(Gaussian Kernel)
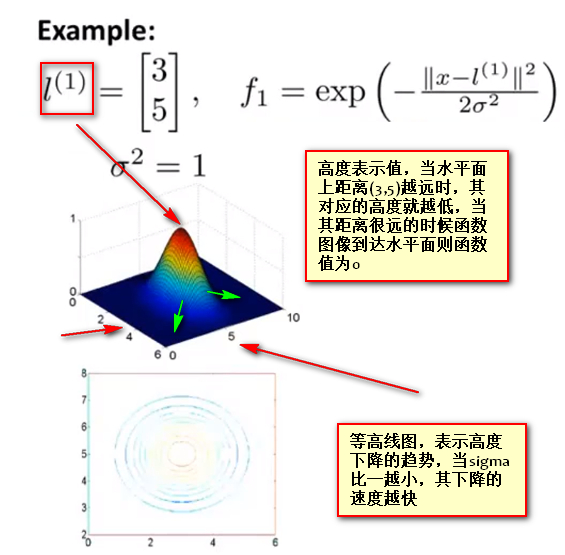
- 假设 地标1 的坐标为(3,5),使用3D图中,即时水平面上对应的坐标为(3,5),核函数使用高斯核,其中 \(\sigma^{2}=1\)
![]()
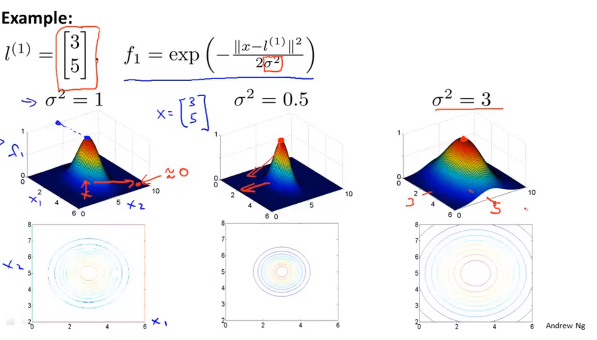
- 等高线表示函数下降的速度 ,以下显示不同\(\sigma\) 对高斯函数陡峭程度的影响,很明显看出 \(\sigma=0.5\) 时下降更快,而 \(\sigma=3\) 时下降速度减缓:
![]()
特征点及边界确定过程
- 规定当\(\theta_0+\theta_{1}f_1+\theta_{2}f_2+\theta_{3}f_3\ge 0\)时输出1
- 假设已经得到参数为\(\theta_0=-0.5,\theta_1=1,\theta_2=1,\theta_3=0\)
- 当给定的训练样本为图中 粉色点 时,此时由于x距离l1较近,所以根据高斯核模型,f1约等于1;而x距离l2,l3都较远,所以f2,f3约等于0
- 此时,将上述参数带入,则\(\theta_0+\theta_{1}f_1+\theta_{2}f_2+\theta_{3}f_3\)的值约等于0.5大于0,因此这个点预测的y值为1
![]()
- 当给定的训练样本为图中 蓝绿色点 时,此时由于x距离l1,l2,l3都较远,根据高斯核模型,f1,f2,f3都约等于0,此时,将上述参数带入,则\(\theta_0+\theta_{1}f_1+\theta_{2}f_2+\theta_{3}f_3\)的值约等于-0.5,因此这个点预测的y值为0
![]()
- 当你对 大量 的训练样本都进行这样的处理,最终会发现一条由大量点组成的 边界 ,显示 距离各个地标何种距离下 输出预测y会为1,否则y会为0.
![]()
- Note 在预测时,采用的不是训练实例本身的特征,而是通过核函数计算出的新特征\(f_1,f_2,f_3\)







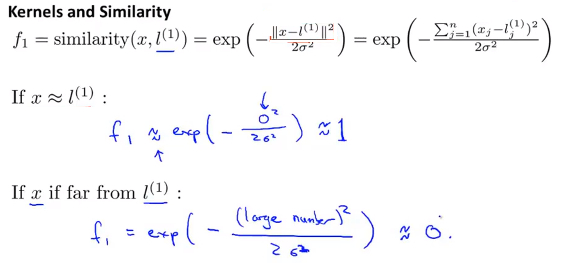



 浙公网安备 33010602011771号
浙公网安备 33010602011771号