[吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释
12.支持向量机
觉得有用的话,欢迎一起讨论相互学习~
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
12.3 大间距分类背后的数学原理- Mathematics Behind Large Margin classification
向量内积
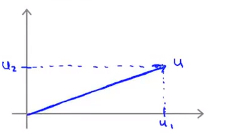
- 假设有两个向量\(u=\begin{bmatrix}u_1\\u_2\\ \end{bmatrix}\),向量\(v=\begin{bmatrix}v_1\\v_2\\ \end{bmatrix}\),其中向量的内积表示为\(u^Tv\).假设\(u_1\)表示为u在坐标轴横轴上的投影,而\(u_2\)表示为u在坐标轴纵轴上的投影,则向量u的欧几里得长度可表示为\(\parallel u \parallel\) , 且有\(\parallel u \parallel=\sqrt{u_1^{2}+u_2^{2}}\)
![]()
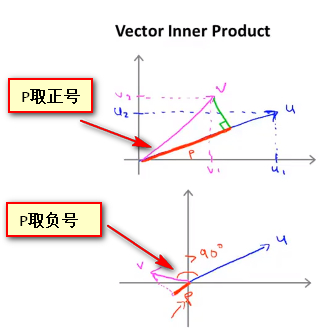
- 对于向量的内积\(u^{T}v\) ,可以视为 v向量在u向量上的投影p乘以u向量的长度,这两者都为实数,且当v向量的投影与u向量同方向时,p取正号,否则p取负号 即有式子 $$u^{T}v=P * \parallel u \parallel=u_1v_1+u_2v_2$$
![]()
向量内积研究SVM目标函数

- 为了更容易分析问题只保留了损失函数的后半部分而去掉了C及其乘积项。 ,原始损失函数如下图:
![]()
- 为简化起见,忽略掉截距,设置损失函数中参数\(\theta_0\)为0,设置特征数n=2. ,则简化后的式子可写为:
![]()
- 因此可以认为SVM的目的就是最小化向量\(\theta\) 范数的平方或者说是长度的平方
\(\theta^{T}x\)的意义
- 给定参数向量 θ 给定一个样本x, 计算其二者的乘积,这其中的含义是什么? 对于\(\theta^{T}x\)其相当于向量内积\(u^{T}v\)
![]()
![]()
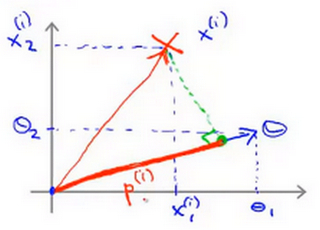
- 首先,对于训练样本\(x^{(i)}\),其在x轴上的取值为\(x^{(i)}_{1}\),其在y轴上的取值为\(x^{(i)}_{2}\) ,此时 将其视为始于原点,终点位于训练样本的向量
- 然后将参数 \(\theta\) 也视为向量且其在横轴上的投影为 \(\theta_1\) ,其在纵轴上的投影为 \(\theta_2\)
- 使用之前的方法,将训练样本投影到参数向量 θ,使用 \(p_{(i)}\)来表示第 i 个训练样本在参数向量\(\theta\)上的投影。 即有 $$\theta{T}x=p_{(i)}\parallel \theta\ \parallel=\theta_1x_1{(i)}+\theta_2x_2$$
![]()
- \(x_{(i)}\)代表从原点出发连接到第i个样本点的向量,是可正可负的,分别表示正样本和负样本;\(p^{(i)}\)表示样本向量\(x_{(i)}\)到参数向量\(\theta\)上的投影,其也是可正可负的,同方向为正负方向为负 ,对于SVM中\(\theta^{T}x^{(i)}\ge1或者\theta^{T}x^{(i)}\le-1\)的约束也可以被 \(p^{(i)}x\ge1\)这个约束所代替
从\(\theta^{T}x\)到大间距
- 首先为方便起见设置 \(\theta_0=0\) ,且只选取两个特征,即\(\theta_1 和 \theta_2\) ,则参数\(\theta\) 可以表示成一条过原点的直线,且 决策界 与\(\theta\)直线垂直。
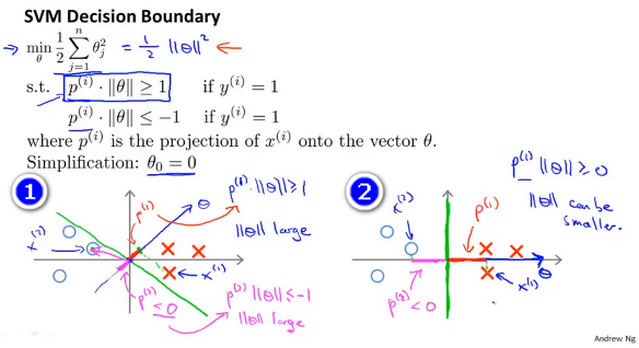
- 反证法 如下图所示(1),y轴右边的表示正样本,而y轴左边的表示负样本,蓝线表示参数\(\theta\),绿线表示决策界 ,很明显这条决策界很不好,因为其与正负样本的间距太小了。 通过将样本投影到\(\theta\)上可以得到p,此时正负样本的||p||都很小,根据SVM的公式||p|| * ||\(\theta\)||>=1,则其必须使||\(\theta\)||很大才能满足条件,这和目标函数希望找到一个小的参数\(\theta\)的目的是矛盾的,这表明这并不是一条好的决策界
- 而图(2)中x在\(\theta\)的投影p就相对的大一些,这样在满足公式\(||p|| * ||\theta||>=1\)需要的||\(\theta\)||就会小一些,这和SVM的优化目标是一致的。所以 好的SVM的优化结果中,决策界的间距一定比较大
![]()






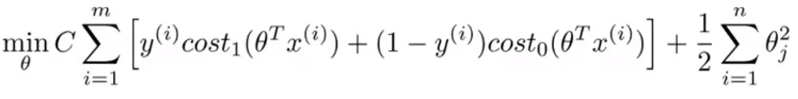



 浙公网安备 33010602011771号
浙公网安备 33010602011771号