[吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距
12.支持向量机
觉得有用的话,欢迎一起讨论相互学习~
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
12.2 大间距的直观理解- Large Margin Intuition
- 人们有时将支持向量机看作是大间距分类器。在这一部分，我将介绍其中的含义，这有助于我们直观理解 SVM 模型的假设是什么样的。以下图片展示的是SVM的代价函数:
最小化SVM代价函数的必要条件
- 如果你有一个正样本,y=1,则只有在z>=1时代价函数\(cost_1(z)\)才等于0。反之,如果y=0,只有在z<=-1的区间里\(cost_0(z)\)函数值为0。这是 支持向量机 的一个有趣性质。
- 事实上，如果你有一个正样本y=1,则仅仅要求\(\theta^{T}x\ge0\),就能将该样本恰当分出.类似地，如果你有一个负样本，则仅需要\(\theta^{T}x\le0\)就可以将负例正确分离。
- 但是，支持向量机的要求更高，对于正样本不仅仅要能正确分开输入的样本，即不仅仅要求\(\theta^{T}x\ge0\)还需要的是比0值大很多，比如大于等于1。对于负样本，SVM也想\(\theta^{T}x\)比0小很多，比如我希望它小于等于-1，这就相当于在支持向量机中嵌入了一个额外的安全因子。或者说安全的间距因子。
正则化参数C与决策边界与决策间距
- 假设把C即正则化参数设定为一个很大的常数，那么为了优化整个SVM损失函数需要把损失项降到最小，即会尽量使乘积项为0，这会使其严格满足以下的约束条件：
\[min\ (C*0+\frac{1}{2}\sum^{n}_{i=1}\theta_j^2)
\]
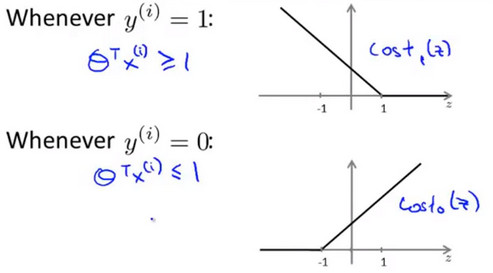
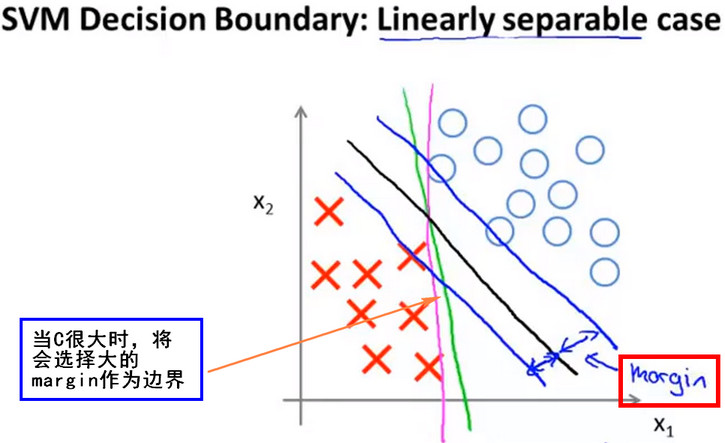
- 线性可分-决策边界
- 可以找到一条直线将正样本和负样本完美地划分开，此例中可以找到多条直线将其分开，下图中的 红线，绿线，黑线 都能将图中点很好的分开，当 正则化参数 很大时则边界线的 间距(margin) 就会很大，即会选择下图中的黑线作为边界线。这使得SVM具有良好的鲁棒性，即会尽量使用大的间距去分离。所以SVM也被称为 大间距分类器(Large margin classifier)
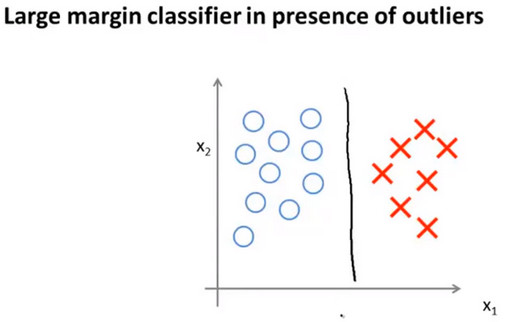
- 当C非常大时，SVM会使用最大的间距将正负样本分开，如下图中的黑线
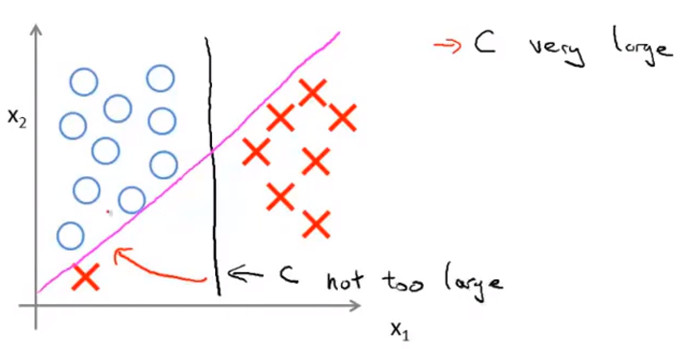
- 但是当C非常大时，SVM为了保证大的边距，对异常点非常敏感，此时边界会变为下图中的紫红色直线，如果此时C没有那么大，SVM不会使用那么大的边距，则边界可能还是黑线
- 当 C 不是非常非常大的时候，它可以忽略掉一些异常点的影响，得到更好的决策界。甚至当你的数据不是线性可分的时候，支持向量机也可以给出好的结果。
- 回顾 C=1/λ，因此：
- C 较大时，相当于 λ 较小，可能会导致过拟合，高方差。
- C 较小时，相当于 λ 较大，可能会导致低拟合，高偏差。
