[吴恩达机器学习笔记]12支持向量机1从逻辑回归到SVM/SVM的损失函数
12.支持向量机
觉得有用的话,欢迎一起讨论相互学习~
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广
12.1 SVM损失函数
从逻辑回归到支持向量机
- 为了描述支持向量机,事实上,我将会从逻辑回归开始展示我们如何一点一点修改来得到本质上的支持向量机。
逻辑回归公式
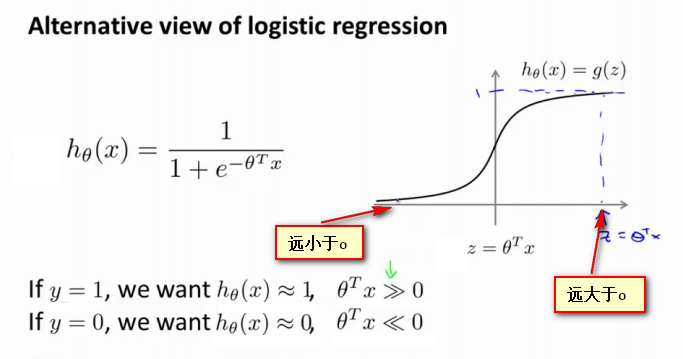
- 逻辑回归公式如下图所示,
![]()
可以看出逻辑回归公式由两个变量x和\(\theta\)构成,其中x表示输入的数据,而\(\theta\)是可学习的变量,如图中右半部分所示,其图像坐标轴横轴为x.\(h_{\theta}(x)\)是关于x的函数。 - 现将z视为新的变量,表示坐标轴横轴和\(\theta\)的乘积,原\(h_{\theta}(x)\)函数变为g(z)函数,z表示原图像上的水平偏移量。
- 如果有一个 y=1 的样本这就意味着当 h(x) 趋近于1时,\(z=\theta^{T}x\)应当远大于0,即z到了函数图像坐标轴的右边,你不难发现此时逻辑回归的输出将趋近于1。相反地,如果我们有另一个样本,即y=0。我们希望假设函数的输出值将趋近于0,这对应于\(z=\theta^{T}x\)远小于 0,即z到了函数图像坐标轴的左边。
逻辑回归损失函数到SVM
- 对于逻辑回归中的每个样本都有损失函数,整个逻辑回归模型的总损失函数即为所有样本损失函数的加和的平均,将逻辑回归的公式带入并展开。
![]()
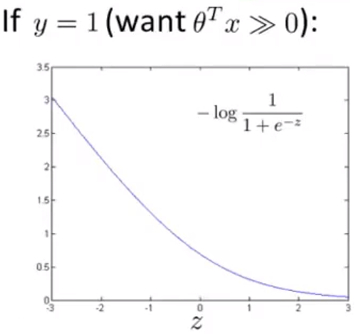
- 当y=1时,并将\(z=\theta^{T}x\)带入其中,有如下图公式:
![]()
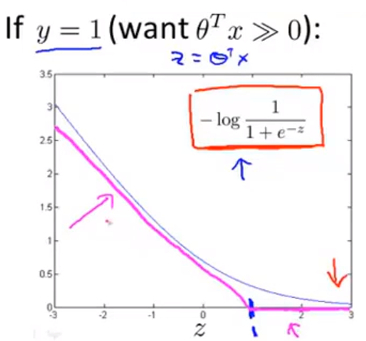
通过这个图像也解释了,当y=1时,为了通过梯度下降得到小的损失函数,总会使\(\theta^{T}x\)非常大的原因。 - 从y=1的损失函数图像进行少量修改就能得到SVM损失函数图像,取z=1的点作为分界点画一条和逻辑回归很接近的 线性图像 得到下图,即 图中玫红色的直线 :
![]()
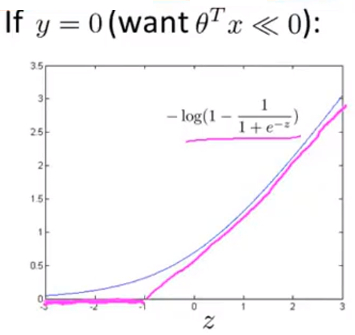
- 当y=0时,并将\(z=\theta^{T}x\)带入其中,有如下图公式:
![]()
- 从y=0的损失函数图像进行少量修改就能得到SVM损失函数图像,取z=-1的点作为分界点画一条和逻辑回归很接近的 线性图像 得到下图,即 图中玫红色的直线 :
![]()
- 对于从逻辑回归中y=1修改而得到的SVM损失函数图像,称其为\(Cost_1(z)\),对于从逻辑回归中y=0修改而得到的SVM损失函数图像,称其为\(Cost_0(z)\).这里的下标是指在代价函数中,对应的 y=1 和 y=0 的情况,拥有了这些定义后,现在,我们就开始构建支持向量机.
构建SVM损失函数公式
- 即对于 逻辑回归 的损失函数分成y=1和y=0两个部分,并将y=1的部分替换为\(Cost_1(z)\),将y=0的部分替换为\(Cost_0(z)\)
![]()
- 但是SVM的损失函数还是和逻辑回归的略有不同,首先从 逻辑回归 处修改后得到的基本公式为:
![]()
- 因为人们在使用逻辑回归和支持向量机时遵循的规则不同,有些地方还需要修改 ,在上述式子中的损失部分和正则化部分都去掉 \(\frac{1}{m}\) 项
- 在逻辑回归中使用\(\lambda\)来平衡样本的损失函数项和正则化项,而在SVM中,使用C来平衡
- 最终的SVM的表达式:
![]()
- Note 最后有别于逻辑回归输出的概率。在这里,当最小化代价函数,获得参数 θ 时,支持向量机所做的是它来直接预测 y 的值等于 1,还是等于 0。所以学习参数 θ 就是支持向量机假设函数的形式。
\[\begin{cases}
1\ \ \ if\ \theta^{T}x\ge0 \\
0\ \ \ otherwise\\
\end{cases}
\]






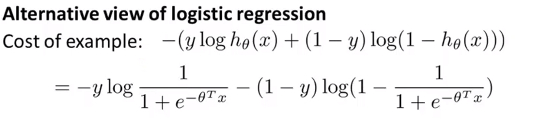

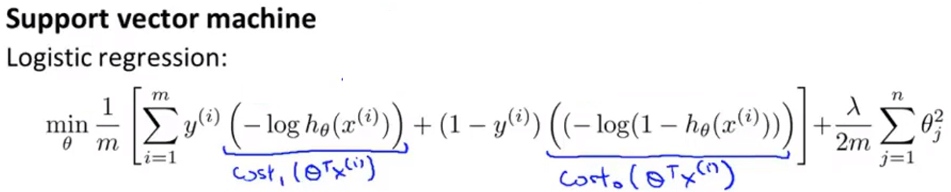
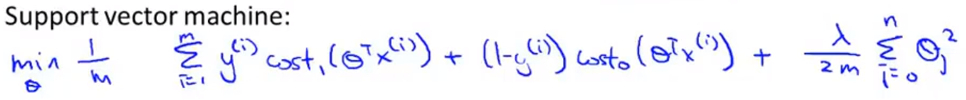
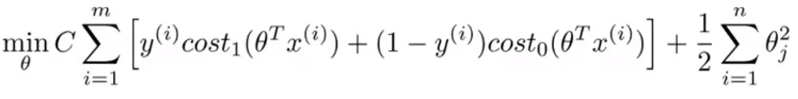

 浙公网安备 33010602011771号
浙公网安备 33010602011771号