[DeeplearningAI笔记]序列模型1.7-1.9RNN对新序列采样/GRU门控循环神经网络
5.1循环序列模型
觉得有用的话,欢迎一起讨论相互学习~
1.7对新序列采样
基于词汇进行采样模型
- 在训练完一个模型之后你想要知道模型学到了什么,一种非正式的方法就是进行一次新序列采样。
- 一个序列模型模拟了任意特定单词序列的概率,对新序列采样即是对概率分布进行采样来生成一个新的单词序列。
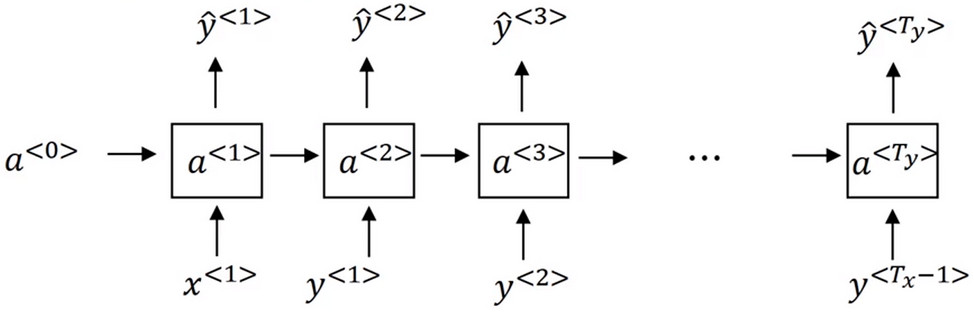
- 假设你的RNN训练模型为:
![]()
- 对于新序列进行采样第一步即是对想要模型生成的第一个词进行采样
- 设置\(a^{<0>}=0,x^{<1>}=0\)从而得到所有可能的输出结果\(\hat{y}^{<1>}\), \(\hat{y}^{<1>}\)是经过softmax层后得到的概率,然后根据经过softmax层后得到的分布进行随机采样。
- 然后继续下一个时间步,但是和训练RNN不同的是,在第二个时间步中输入的不是正确的\(y^{<1>}\),而是把刚刚采样得到的\(\hat{y}^{<1>}\)作为下一个时间步的输入。
- 然后对第二个时间步的预测得到的输出\(\hat{y}^{<2>}\)进行采样并作为第三个时间步的输入...直到达到最后一个时间步。
![]()
- 对于采样完成有两种判定方法:
- 一直在字典集中进行采样,直到得到
标识,这表明可以停止采样了。 - 如果在时间步的结尾,字典中没有这个词,你可以从20个或100个或其他单词中进行采样,然后一直抽样下去,直到达到设定的时间步。但是如果在此过程中又出现了 unknown word,则可以进行重采样,直到得到一个不是一个未知标识的词。如果不介意UNK的话,也可以忽略这些未知的单词。
- 一直在字典集中进行采样,直到得到
基于字符进行采样模型
- 根据实际问题,还可以建立基于字符的RNN结构,你的字典仅包含从a到z的字母,可能还会有空格符,数字0-9,还有大写的A-Z字母,还有数据集中出现的特殊字符。最终使用这些字符组成你的字典。
- 这样每次RNN推断的输出都是字母而不是单独的词汇。
- 优点与缺点
- 优点
- 优点是不会出现未知的标识
- 缺点
- 缺点是使用字符进行采样的模型会得到很多很长的序列
- 因为一句话中的英文单词仅有几十个,但是字符的长度却有很多个,这样使得RNN的长度过大,使得其不可以捕捉长范围的关系,而且训练起来计算成本比较高昂。
- 所以现有的RNN都是使用基于单词的采样,但是随着计算机性能越来越高,使用基于字符进行采样也是一种趋势。
- 优点
序列生成
- 使用新闻的语料库作为训练集,则生成的序列带有明显的新闻语感。
- 使用莎士比亚的语料库作为训练集,则生成的序列带有明显的莎士比亚风格。
![]()
1.8RNN的梯度消失vanishing gradient
- 基本的RNN有一个很大的问题,就是梯度消失问题
梯度消失vanishing gradient
- 示例
- THe cat, which already ate a bunch of food that was delicious ....was full.
- THe cats, which already ate a bunch of food that was delicious ....were full.
- 注意句式中的单复数问题,cat作为主语,则使用was,cats作为主语,则使用were.
- 主语和谓语的单复数关系,因为有从句(即主语和谓语之间的距离可以足够长)的关系,在时间上往往具有 很长时间的依赖效应(long-term dependencies)
- 但是普通的RNN并不擅长捕捉这种长期依赖效应(因为具有梯度消失的问题)。
梯度爆炸exploding gradients
- 梯度不仅仅会指数级别的下降,也会指数级别的上升--即梯度爆炸(exploding gradients),导致参数的数量级及其巨大会看见许多NaN或者不是数字的情况--这意味着网络的计算出现了数值溢出。
- 如果出现了梯度爆炸的问题,一个解决方法就是使用梯度修剪(gradient clipping).即--设置一个梯度的天花板,梯度不能超过这个阈值,并对梯度进行缩放。
1.9GRU Gate Recurrent Unit门控循环神经网络
-
GRU网络改变了RNN的隐层结构,可以捕捉深层连接,并改善了梯度消失问题。
-
\(a^{t}=g(W_{a}[a^{t-1},x^{t}]+b_{a})\)
[1] Cho K, Van Merrienboer B, Bahdanau D, et al. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches[J]. Computer Science, 2014.
[2] Chung J, Gulcehre C, Cho K H, et al. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling[J]. Eprint Arxiv, 2014.
门控循环神经网络单元GRU
- The cat , which already ate ..., was full
- 为了记住话语中cat是单数还是复数,在时间T上需要使用记忆细胞memory cell 记住cat这个单词,并且 \(c^{t}=a^{t}\)
- 在每一个时间步t,都将用一个候选值\(\breve{c}^{t}\)重写记忆细胞的值
- 其中:
\[\breve{c}^{t}=Tanh(W_{c}[c^{t-1},x^{t}]+b_{c})[1]
\]
- GRU中真正重要的思想是,GRU中有一个门Gate(\(\gamma_u\)) 这是一个0到1之间的值
-
\[\gamma_u=\sigma(W_{u}[c^{t-1},x^{t}]+b_{u})[2] \]
-
- [1]式是\(\breve{c}^{t}\)的更新公式,[2]式计算的值用以控制是否采用[1]式进行更新
- 在此例中如果cat变为cats \(\breve{c}^{t}\)用以控制was和were的值,而\(\gamma_u\)用以控制 在何时将was变为were
- $$C^{t}=\gamma_u * \breve{C}^{t}+(1-\gamma_u) * C^{t-1}$$
如果\(\gamma_u=1\)则\(C^{t}=\breve{C}^{t}\),\(\gamma_u=0\)则\(C^{t}=C^{t-1}\),即时间步没有扫到was时,\(\gamma_u一直=0,此时C^{t}=c^{t-1}\),则C一直等于旧的值。而当时间步扫到"was"时,\(\gamma_u=1\),此时\(C^{t}=\breve{C}^{t}\)
![]()
- $$C^{t}=\gamma_u * \breve{C}^{t}+(1-\gamma_u) * C^{t-1}$$
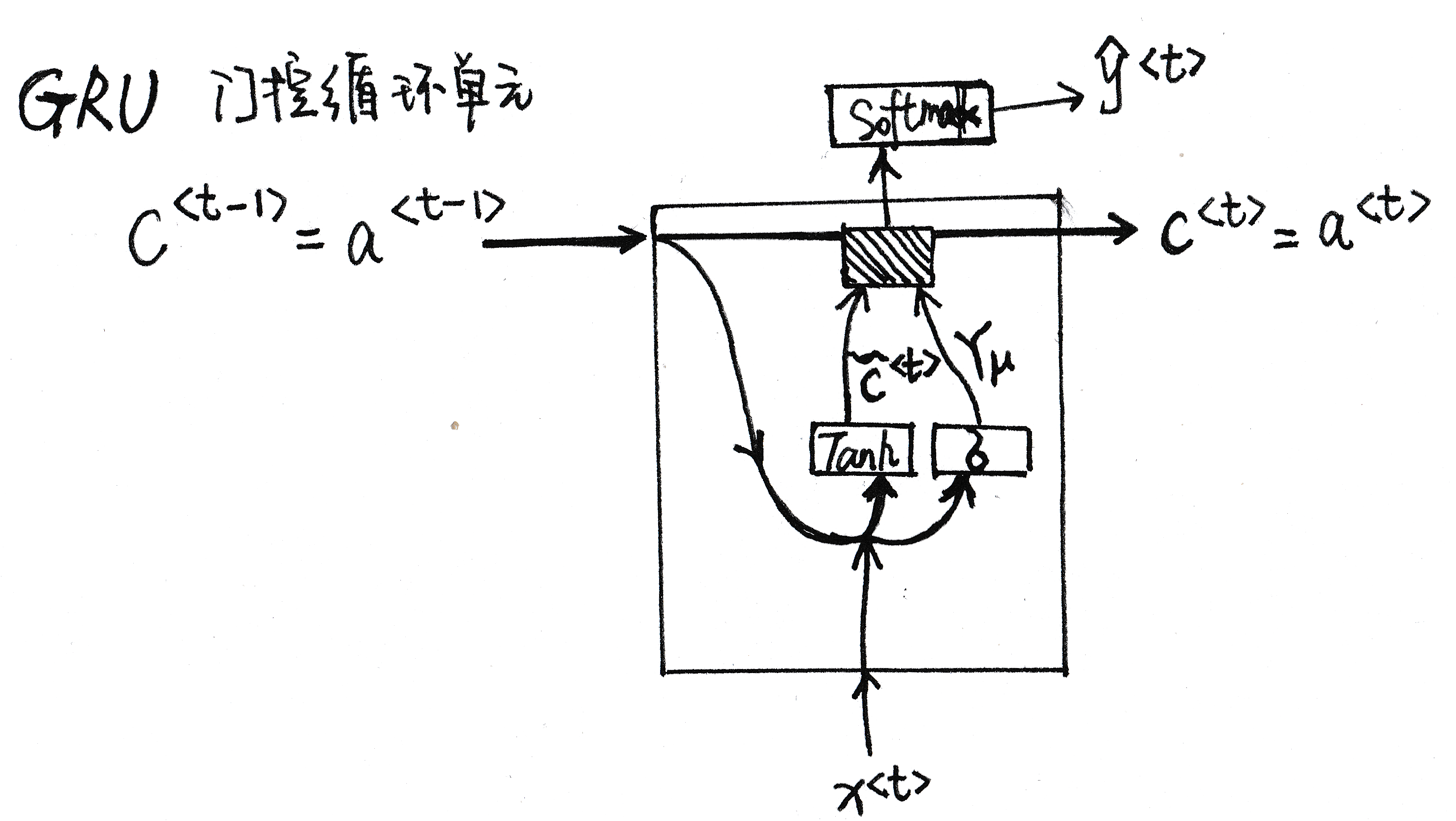
GRU计算过程
- GRU单元输入\(C^{t-1}\)对应于上一个时间步,先假设其正好等于\(a^{t-1}\), 然后\(x^{t}\)也作为输入,然后把这两个用合适的权重结合在一起再用Tanh计算,算出\(\breve{c}^{t}\)即\(c^{t}\)的替代值
- 再用一个不同的参数集,通过\(\sigma\)函数计算出\(\gamma_u\),即更新门。
- 最后所有的值通过另一个运算符结合:
$$C^{t}=\gamma_u * \breve{C}^{t}+(1-\gamma_u) * C^{t-1}$$
,其输入一个门值,新的候选值和旧的记忆细胞值,得到记忆细胞的新值\(c^{t}=a^{t}\),也可以把这个值传入Softmax单元中,并计算出预测序列\(\hat{y}^{t}\)
![]()
GRU优点
- 当你从左往右扫描一整个句子时,控制记忆细胞"不更新不更新不更新... 更新 "
- 因为门的值很容易取到0,只要激活函数的输入是一个很大的负数,则激活函数的输出值就是一个很接近与0的值。所以 \(C^{t}=\gamma_u * \breve{C}^{t}+(1-\gamma_u) * C^{t-1}\) 中\(C^{t}=C^{t-1}\)则即是经过很多的时间步,记忆神经细胞的值都会很好的维持了下来--这样就避免了梯度消失的问题。这样可以保证RNN运行在十分庞大的依赖词上。
Note
- \(C^{t},\breve{C}^{t},\gamma_u\)是具有一样的维度的向量,其中维度和隐藏层的激活值的个数相等。
完整GRU











 浙公网安备 33010602011771号
浙公网安备 33010602011771号