[DeeplearningAI笔记]序列模型1.3-1.4循环神经网络原理与反向传播公式
5.1循环序列模型
觉得有用的话,欢迎一起讨论相互学习~
1.3循环神经网络模型
为什么不使用标准的神经网络
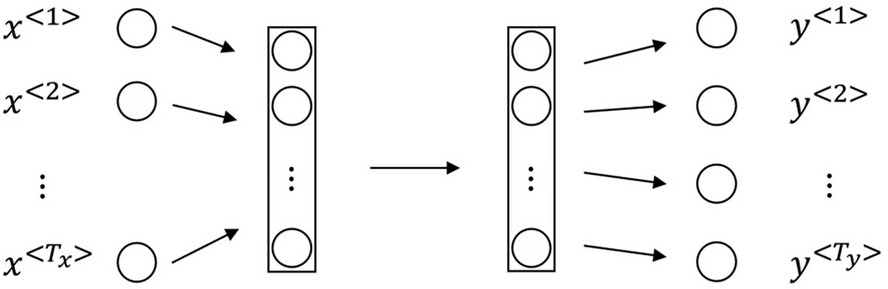
- 假如将九个单词组成的序列作为输入，通过普通的神经网网络输出输出序列，
- 在不同的例子中输入数据和输出数据具有不同的长度，即每个数据不会有一样的长度
- 也许每个语句都有最大长度，能够通过Padding 的方式填充数据，但总体来说不是一个好的表达方式。
- 不共享从文本的不同位置上学到的特征
- 例如普通神经网络可以学习到Harry这个单词出现在\(x^{<1>}\)的位置，但是如果Harry这个单词出现在\(x^{<4>}\)的位置，普通的神经网络不能识别的出来。
- 输入量巨大，如果词典中最大的单词量是1W的话，则单词的one-hot表示向量将是一个1W维的数据。而一个训练语句中的单词数为\(T_{x}\),则输入数据的维度为\(T_{x} * 1W\)此数据维度是十分巨大的。
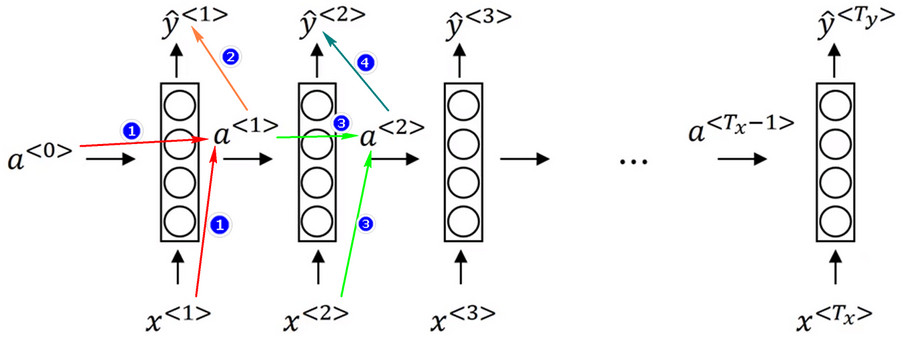
循环神经网络模型
\[a^{<0>}=\vec{0}
\]
\[a^{<1>}=g(W_{aa}a^{<0>}+W_{ax}X^{<1>}+b_{a})
\]
\[//g表示非线性激活函数(Tanh/ReLU)
\]
\[\hat{y}^{<1>}=g(W_{ya}a^{<1>}+b_{y})
\]
\[//g表示非线性激活函数,但是不一定要与上面的g相同(Sigmoid)
\]
\[a^{<T_{x}>}=g(W_{aa}a^{<T_{x}-1>}+W_{ax}X^{<T_{x}>}+b_{a})
\]
\[\hat{y}^{<T_{x}>}=g(W_{ya}a^{<T_{x}>}+b_{y})
\]
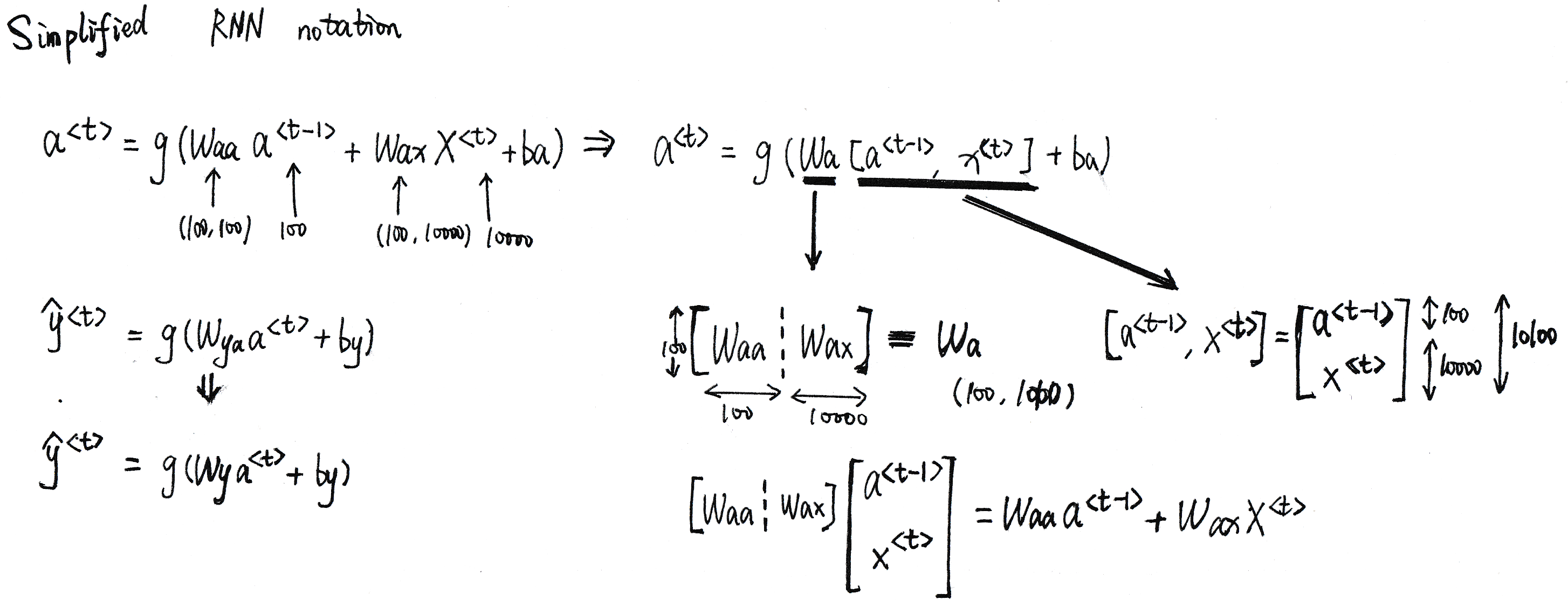
简化循环神经网络数学公式
- 将\(W_{aa}和W_{ax}合并成一个大的矩阵W_{a}，将a^{<t-1>}和X^{<t>}合并成[a^{<t-1>},X^{<t>}]\)
具体如下图所示:
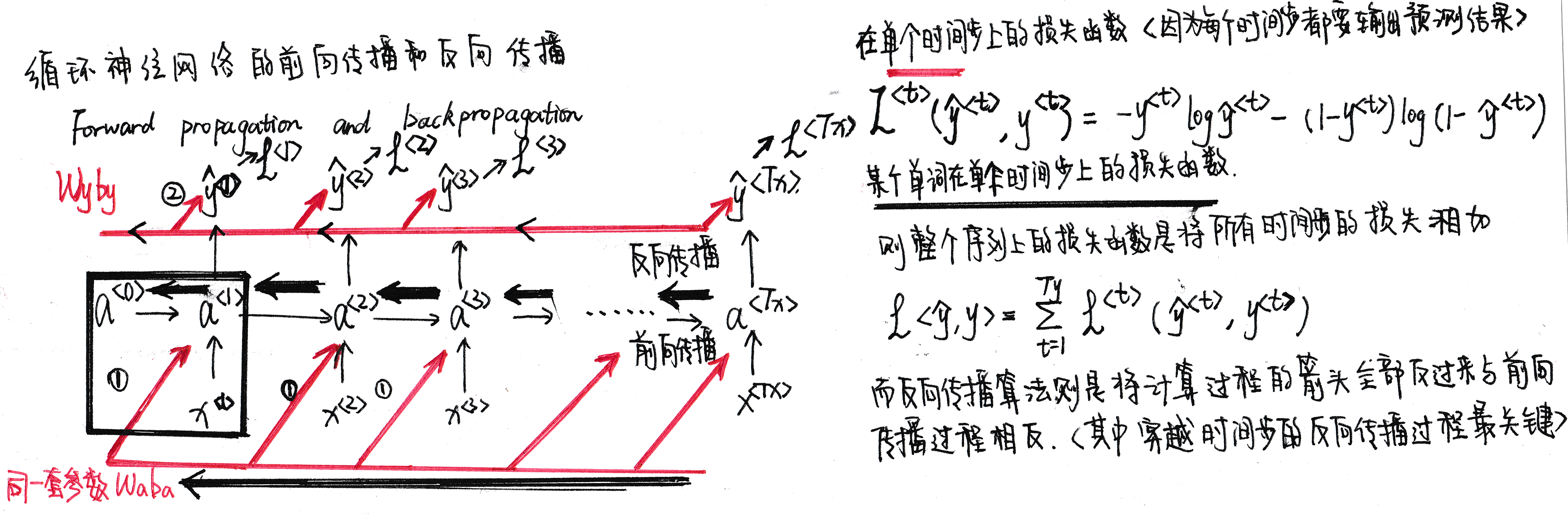
1.4通过时间的反向传播Backpropagation through time
