[DeeplearningAI笔记]第二章2.6-2.9Momentum/RMSprop/Adam与学习率衰减
[DeeplearningAI笔记]第二章2.6-2.9Momentum/RMSprop/Adam与学习率衰减
觉得有用的话,欢迎一起讨论相互学习~
2.6 动量梯度下降法(Momentum)
-
另一种成本函数优化算法,优化速度一般快于标准的梯度下降算法.
-
基本思想:计算梯度的指数加权平均数并利用该梯度更新你的权重
-
假设图中是你的成本函数,函数形象如图所示.其中红点所示就是你的最低点.使用常规的梯度下降方法会有摆动，这种波动减缓了你训练模型的速度,不利于使用较大的学习率,如果学习率使用过大则可能会偏离函数的范围.为了避免摆动过大,你需要选择较小的学习率.
- 而是用Momentum梯度下降法,我们可以在纵向减小摆动的幅度在横向上加快训练的步长.
基本公式
\[Vd_{w}=\beta Vd_{w}+(1-\beta)d_{w}
\]
\[Vd_{b}=\beta Vd_{b}+(1-\beta)d_{b}
\]
- 在纵轴方向上,你希望放慢一点,平均过程中,正负数相互抵消,平均值接近于零.
- 横轴方向所有的微分都指向于横轴方向,所以横轴的平均值仍较大.
- 横轴方向运动更快,纵轴方向摆动幅度变小.
- 两个超参数 \(\alpha控制学习率,\beta控制指数加权平均数,\beta最常用的值是0.9\)
- 此处的指数加权平均算法不一定要使用带修正偏差,因为经过10次迭代的平均值已经超过了算法的初始阶段,所以不会受算法初始阶段的影响.
2.7 RMSprop(均方根)
- RMSprop (root mean square prop),也可以加速梯度下降.
- 对于梯度下降,横轴方向正在前进,但是纵轴会有大幅度的波动.我们现将横轴代表参数W,纵轴代表参数b.横轴也可以代表\(W_{[1]},W_{[2]},W_{[3]}...W_{[n]}\),但是为了便于理解,我们将其称之为b和W.
- 公式
\[S_{dw}=\beta S_{dw}+(1-\beta)(dw)^{2}
\]
\[S_{db}=\beta S_{db}+(1-\beta)(db)^{2}
\]
\[接着RMSprop会这样更新参数值
\]
\[W=W-\alpha \frac{dw}{\sqrt{S_{dw}}}
\]
\[b=b-\alpha \frac{db}{\sqrt{S_{db}}}
\]
- w的在横轴上变化变化率很小,所以dw的值十分小,所以\(S_{dw}\)也小,而b在纵轴上波动很大,所以斜率在b方向上特别大.所以这些微分中,db较大,dw较小.这样W除数是一个较小的数,总体来说,W的变化很大.而b的除数是一个较大的数,这样b的更新就会被减缓.纵向的变化相对平缓.
- 注意:这里的W和b标记只是为了方便展示,在实际中这是一个高维的空间,很有可能垂直方向上是W1,W2,W5..的合集而水平方向上是W3,W4,W6...的合集.
- 实际使用中公式建议为:
\[W=W-\alpha \frac{dw}{\sqrt{S_{dw}+\epsilon}}
\]
\[b=b-\alpha \frac{db}{\sqrt{S_{db}+\epsilon}}
\]
- 为了保证实际使用过程中分母不会为0.
- 主要目的是为了减缓参数下降时的摆动,并允许你使用一个更大的学习率 \(\alpha\),从而加快你的算法速率.
2.8 Adam算法
- Adam 算法基本原理是将Momentum和RMSprop结合在一起.
算法原理
超参数取值
- 学习率 \(\alpha\) 十分重要,也经常需要调试.
- \(\beta_{1}\) 常用的缺省值是0.9
- \(\beta_{2}\) Adam的发明者推荐使用的数值是0.999
- \(\epsilon 的取值没有那么重要,Adam论文的作者建议为\epsilon=10^{-8}\)
- 在实际使用中,\(\beta_{1},\beta_{2},\epsilon 都是使用的推荐的缺省值,一般调整的都是学习率\alpha\)
- Adam: Adaptive Moment Estimation(自适应估计时刻)
2.9 学习率衰减(learning rate decay)
- 加快学习算法的一个办法就是随时间慢慢减少学习率,我们将之称为学习率衰减(learning rate decay)
概括
- 假设你要使用mini-batch梯度下降法,mini-batch数量不大,大概64或者128个样本,但是在迭代过程中会有噪音,下降朝向这里的最小值,但是不会精确的收敛,所以你的算法最后在附近摆动.,并不会真正的收敛.因为你使用的是固定的 \(\alpha\),在不同的mini-batch中有杂音,致使其不能精确的收敛.
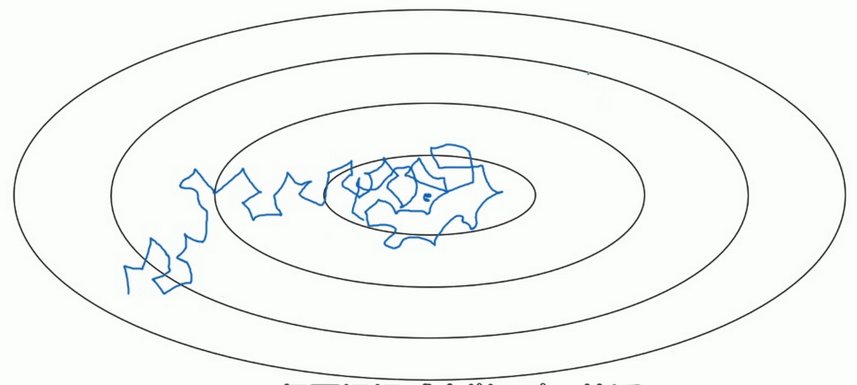
- 但如果能慢慢减少学习率 \(\alpha\) 的话,在初期的时候,你的学习率还比较大,能够学习的很快,但是随着 \(\alpha\) 变小,你的步伐也会变慢变小.所以最后的曲线在最小值附近的一小块区域里摆动.所以慢慢减少 \(\alpha\) 的本质在于在学习初期,你能承受较大的步伐, 但当开始收敛的时候,小一些的学习率能让你的步伐小一些.
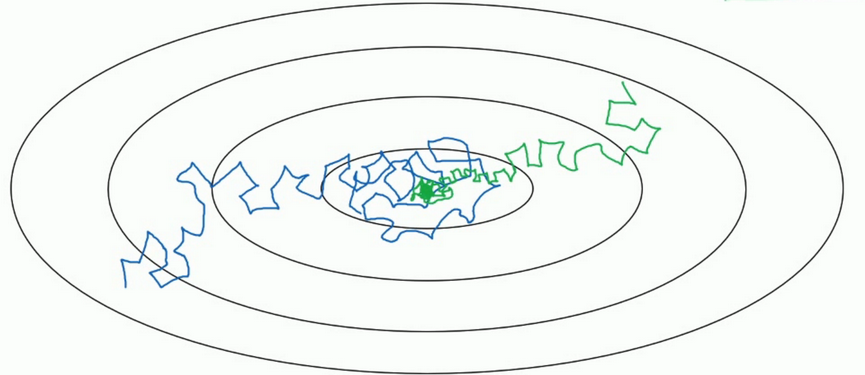
细节
- 一个epoch表示要遍历一次数据,即就算有多个mini-batch,但是一定要遍历所有数据一次,才叫做一个epoch.
- 学习率 \(\alpha ,其中 \alpha_{0}表示初始学习率, decay-rate是一个新引入的超参数\) :
\[\alpha = \frac{1}{1+decay-rate*epoch-num}*\alpha_{0}
\]
其他学习率衰减公式
指数衰减
\[\alpha = decay-rate^{epoch-num}*\alpha_{0}
\]
\[\alpha = \frac{k}{\sqrt{epoch-num}}*\alpha_{0}其中k是超参数
\]
\[\alpha = \frac{k}{\sqrt{t}}*\alpha_{0}其中k是超参数,t表示mini-batch的标记数字
\]
