[DeeplearningAI笔记]第二章2.1-2.2mini-batch梯度下降法
[DeeplearningAI笔记]第二章2.1-2.2mini-batch梯度下降法
觉得有用的话,欢迎一起讨论相互学习~
2.1 mini-batch gradient descent mini-batch梯度下降法
- 我们将训练数据组合到一个大的矩阵中
\[X=\begin{bmatrix}x^{(1)}&x^{(2)}&x^{(3)}&x^{(4)}&x^{(5)}...x^{(n)}\end{bmatrix}
\]
\[Y=\begin{bmatrix}y^{(1)}&y^{(2)}&y^{(3)}&y^{(4)}&y^{(5)}...y^{(n)}\end{bmatrix}
\]
- 在对整个数据集进行梯度下降时,你要做的是,你必须训练整个训练集,然后才能进行一步梯度下降法.然后需要重新训练整个数据集,才能进行下一步梯度下降法.所以你在训练整个训练集的一部分时就进行梯度下降,你的算法速度会更快.你可以把训练集分割为小一点的子训练集.这些小的训练集被称为mini-batch.每次训练一个mini-batch后就对模型的权值进行梯度下降的算法叫做mini-batch梯度下降法.
2.2 理解mini-batch梯度下降
-
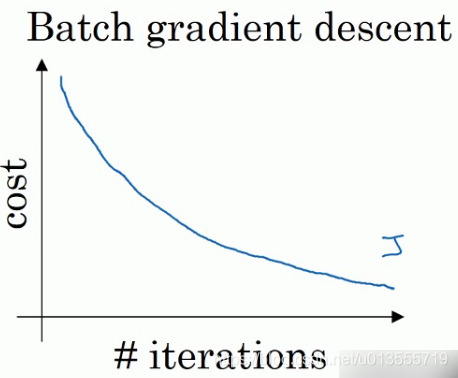
在batch梯度下降中,每次迭代你都需要遍历整个训练集,可以预期正常情况下每次迭代的成本函数都会下降.
-
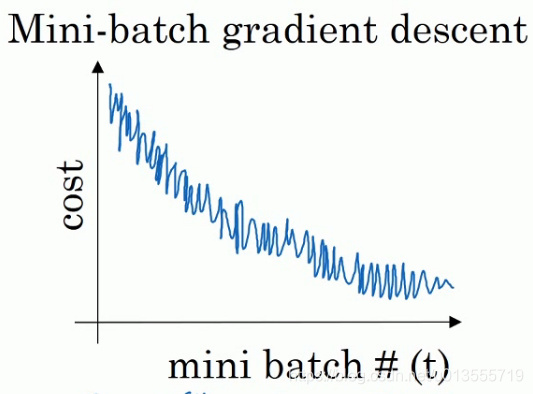
使用mini-batch梯度下降法时,会发现cost并不是每次迭代都下降的,看到的图像可能是以下这种情况.总体走向朝下但是有更多的噪声.
你需要决定的变量之一就是mini-batch的大小,m就是训练集的大小.
-
极端情况下,如果m=mini-batch,其实就是batch梯度下降法.在这种极端情况下,假设mini-batch大小为1一次只处理一个,就有了新的算法,叫做随机梯度下降法.
-
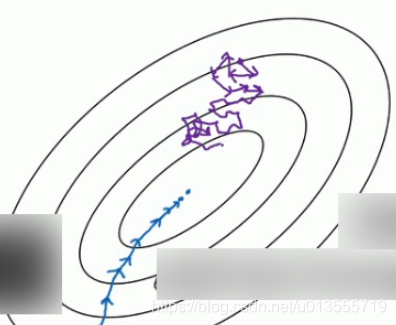
看两个极端情况下,成本函数的优化情况:
- 假设图中蓝点是最小值点,其中batch梯度下降从某处开始,相对噪声低些,幅度也大一些:
- 假设图中蓝点是最小值点,其中batch梯度下降从某处开始,相对噪声低些,幅度也大一些:
-
对于随机剃度下降,你只对一个样本进行梯度下降,大部分时候你向着全局最小值靠近,但是有时候你会偏离方向,因为那个样本恰好给你指的方向不正确.因此随机梯度下降法是有很多噪声的.平均来看会向着正确的方向,不过有时候也会方向错误.
-
因为随机梯度下降法永远不会收敛,而是会一直在最小值附近波动.但它并不会达到最小值并停留于此.
不同的梯度下降算法的利和弊
- 每次迭代需要处理大量训练样本,该算法主要弊端是特别是在训练样本数量巨大的时候,单次迭代耗时太长,如果训练样本不大,batch梯度下降法运行的很好.
- 相反如果使用随机梯度下降法,每次只训练一个训练样本,通过减少学习率,噪声也会相应的减少.但是其一大缺点是:你会失去所有向量化带给你的加速.
