【转】异常值处理

异常值处理

觉得有用的话,欢迎一起讨论相互学习~

版权声明：本文为CSDN博主「sljwy」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/sinat_23971513/article/details/114918790

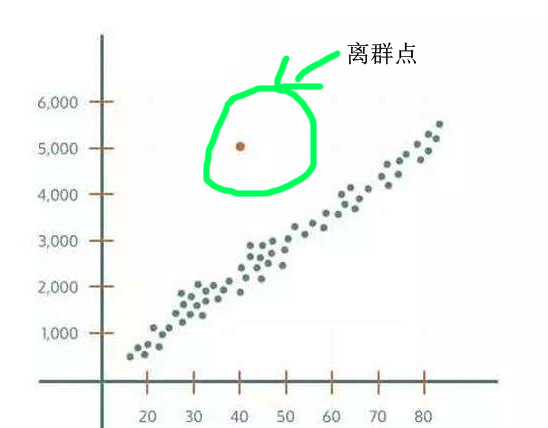
什么样的值是异常值？

简单来说，即在数据集中存在不合理的值，又称离群点。

我们举个例子，做客户分析，发现客户的年平均收入是80万美元。 但是，有两个客户的年收入是4美元和420万美元。 这两个客户的年收入明显不同于其他人，那这两个观察结果将被视为异常值。

什么会引起异常值呢？

每当我们遇到异常值时，处理这些异常值的理想方法就是找出引起这些异常值的原因。 处理它们的方法将取决于它们发生的原因， 异常值的原因可以分为两大类：

人为错误
自然错误

数据输入错误

人为错误（如数据收集，记录或输入过程中导致的错误）会导致数据中的异常值。 例如：客户的年收入是10万美元，但意外地，数据输入操作附加一个零。 现在的收入就是100万美元，是10倍。 显然，与其他人相比，这将是异常值。

测量误差

这是异常值最常见的来源。 当使用的测量仪器出现故障时，会引起这种情况。 例如：有10台称重机。 其中9个是正确的，1个是错误的。 故障机器上的人员测量重量将高于或低于组内其余人员。 在故障机器上测量的重量可能导致异常值。

实验误差

异常值的另一个原因是实验误差。 例如：在7名跑步者的100米冲刺中，有一名选手错过了跑的口令，让他开始延迟。 因此，这使得跑步者的跑步时间比其他跑步者要多， 总运行时间可能是一个异常值。

故意异常值

通常在自我报告的措施中涉及敏感数据。 例如：通常青少年报告酒量，只有其中一小部分报告实际价值，这里的实际值可能看起来像异常值，因为其余的青少年正在假值。

数据处理错误

无论何时执行数据挖掘，我们从多个来源提取数据。 某些操作或提取错误可能会导致数据集中的异常值。

抽样错误

例如，衡量运动员的身高，错误地在样品中包括几名篮球运动员。 这种包含可能会导致数据集中的异常值。

自然异常值

当异常值不是人为的（由于错误），它是一个自然的异常值。 例如：注意到其中一家著名的保险公司，前50名财务顾问的表现远远高于其他人。 令人惊讶的是，这不是由于任何错误。 因此，每当与顾问一起执行任何数据挖掘活动时，我们都会分别对待此细分。

判别方法：

1.简单统计分析

对属性值进行一个描述性的统计，从而查看哪些值是不合理的。比如对年龄这个属性进行规约：年龄的区间在[0:200]，如果样本中的年龄值不再该区间范围内，则表示该样本的年龄属性属于异常值。

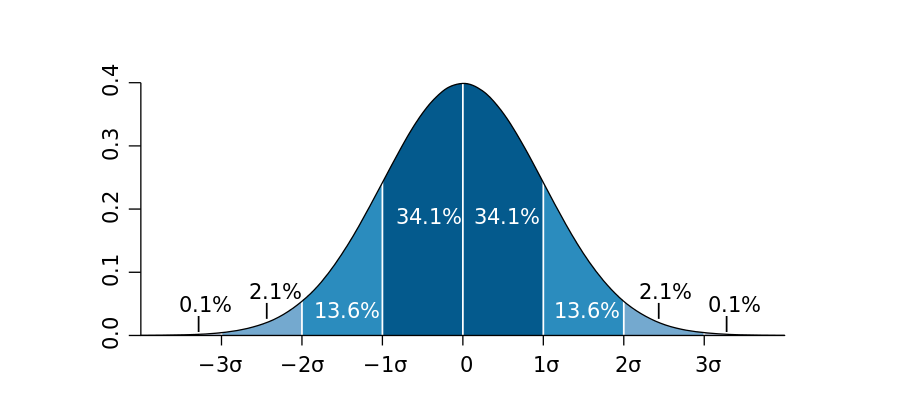
2. 3δ原则

当数据服从正态分布：

根据正态分布的定义可知，距离平均值3δ之外的概率为 P(|x-μ|>3δ) <= 0.003 ，这属于极小概率事件，在默认情况下我们可以认定，距离超过平均值3δ的样本是不存在的。 因此，当样本距离平均值大于3δ，则认定该样本为异常值。

当数据不服从正态分布：

当数据不服从正态分布，可以通过远离平均距离多少倍的标准差来判定，多少倍的取值需要根据经验和实际情况来决定。

3．箱型图分析

箱线图（Boxplot）也称箱须图（Box-whisker Plot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。

具体含义如下，首先计算出第一四分位数（Q1）、中位数、第三四分位数（Q3）。
中位数我们都知道，就是将一组数字按从小到大的顺序排序后，处于中间位置（也就是50%位置）的数字。
同理，第一四分位数、第三四分位数是按从小到大的顺序排序后，处于25%、75%的数字。

令 IQR=Q3−Q1，那么 Q3+1.5(IQR) 和 Q1−1.5(IQR) 之间的值就是可接受范围内的数值，这两个值之外的数认为是异常值。

在Q3＋1.5IQR（四分位距）和Q1-1.5IQR处画两条与中位线一样的线段，这两条线段为异常值截断点，称其为内限；在Q3＋3IQR和Q1－3IQR处画两条线段，称其为外限。
处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值(li)的异常值extreme outliers。这种异常值的检测方法叫做Tukey’s method。

从矩形盒两端边向外各画一条线段直到不是异常值的最远点 表示该批数据正常值的分布区间点，表示该批数据正常值的分布区间。

一般用“〇”标出温和的异常值，用“＊”标出极端的异常值。

首先我们定义下上四分位和下四分位。

上四分位我们设为 U，表示的是所有样本中只有1/4的数值大于U
同理，下四分位我们设为 L，表示的是所有样本中只有1/4的数值小于L

那么，上下界又是什么呢？

我们设上四分位与下四分位的插值为IQR，即：IQR=U-L

那么，上界为 U+1.5IQR ，下界为： L - 1.5IQR

箱型图选取异常值比较客观，在识别异常值方面有一定的优越性。

异常值的处理方法常用有四种：

1.删除含有异常值的记录

2.将异常值视为缺失值，交给缺失值处理方法来处理

3.用平均值来修正

4.不处理

代码实现

import pandas as pd
import numpy as np
from collections import Counter

def detect_outliers(df,n, features):

    outlier_indices = []

    for col in features:
        Q1 = np.percentile(df[col], 25)
        Q3 = np.percentile(df[col], 75)

        IQR = Q3 - Q1

        outlier_step = 1.5 * IQR

        outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index

        outlier_indices.extend(outlier_list_col)

    outlier_indices = Counter(outlier_indices)
    multiple_outliers = list( k for k, v in outlier_indices.items() if v > n)

    return multiple_outliers

df = pd.read_csv("data.csv")
Outliers_to_drop = detect_outliers(df, 2 ["Col1", "Col2", "Col3", "Col4"])
df = df.drop(Outliers_to_drop, axis=0).reset_index(drop=True)