DNA序列编码中Hairpin的定义和计算
DNA序列编码中Hairpin的定义和计算
觉得有用的话,欢迎一起讨论相互学习~
参考文献
[1] 张凯. DNA计算核酸编码优化及算法设计[D]. 2008.
[2] Shin, Soo Yong , et al. "Multiobjective evolutionary optimization of DNA sequences for reliable DNA computing." IEEE Transactions on Evolutionary Computation 9.2(2005):143-158.
[3] Shin, Soo Yong , I. H. Lee , and B. T. Zhang . "Evolutionary Multi-Objective Optimization for DNA Sequence Design." (2008).
[4] Shin, Soo Yong , et al. "Evolutionary sequence generation for reliable DNA computing." Congress on Evolutionary Computation IEEE, 2002.
[5] 饶泽书. 基于多目标粒子群的DNA编码算法研究[D]. 2018.
发卡结构约束
[ * ]定义
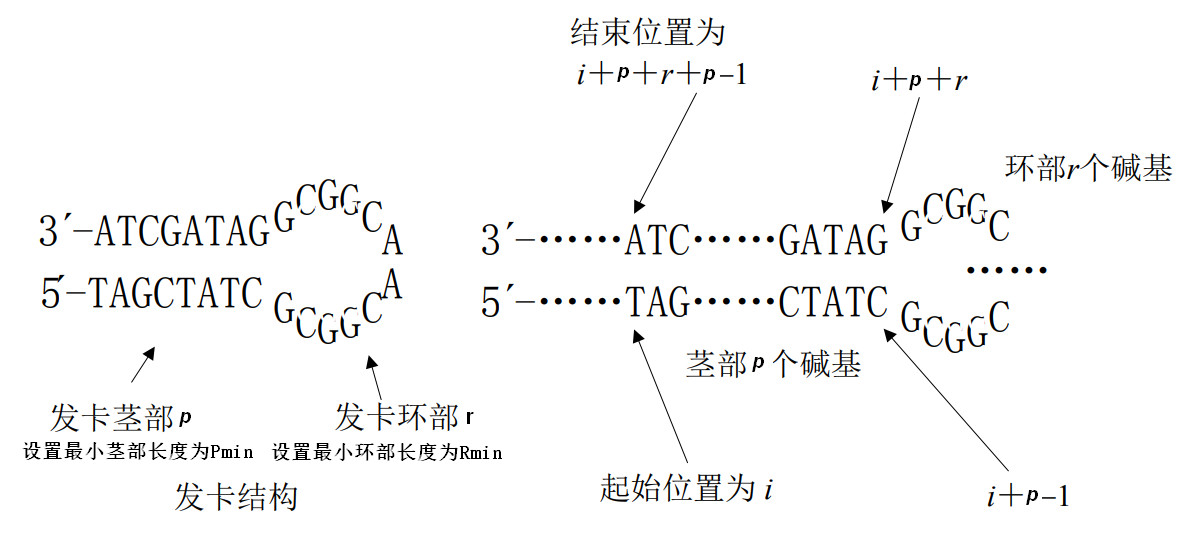
单链 DNA 分子产生二级结构通常由自身反向折叠而形成,发卡结构为典型的自身折叠结构.许多以特异性杂交反应为基础的 DNA 计算模型,都要求避免单链 DNA 形成二级
结构,这样单链 DNA 分子才能和自身的补链充分有效的发生特异性杂交[1]。
\[Hairpin( x ) = \sum _ { s = S _ { \mathrm { min } } } ^ { \left( l - R _ { \mathrm { min } } \right) / 2 } \sum _ { r = R _ { \mathrm { min } } } ^ { l - 2 s } \sum _ { i = 1 } ^ { l - 2 s - r } T \left( \sum _ { j = 1 } ^ { s } b p \left( x _ { s + i - j} , x _ { s + i + r + j-1} \right) , \frac { s } { 2 } \right)
\]
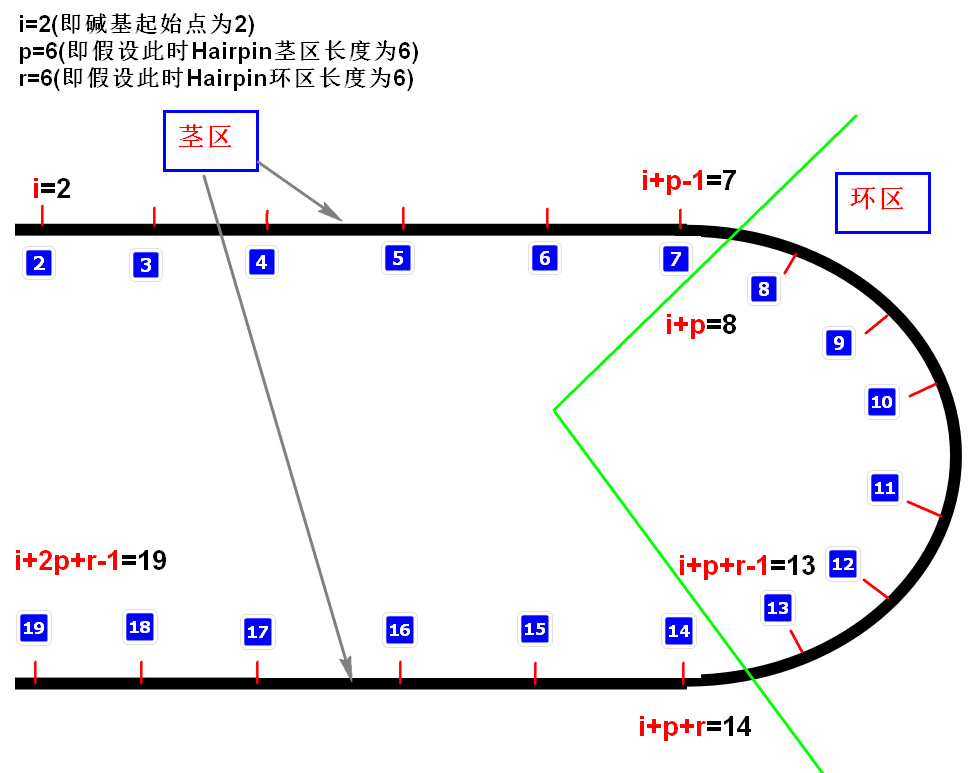
- 式中s为茎长,Smin为设定的最小茎长。r为环长,Rmin为设定的最小环长,L表示DNA序列长度。在本文中,设置Smin=6,Rmin=6
- T表示阈值函数,T(x,y),只有在x>y时T(x,y)=x;否则T(x,y)=0,此处表示只有连续匹配达到了当前茎区数量的1/2(即>\(\frac{S}{2}\))才能算作为茎区的结构。
- bp(x,y)函数表示DNA序列中x和y位置的碱基相互互补的个数,如果相互互补即为1,否则记为0.
- s表示遍历茎区可能长度,其中 茎区最小长度为人为设定的Smin ,而 茎区最大长度是当环区长度取得最小值Rmin时的茎区长度(l-Rmin)/2
- r表示遍历环区可能长度,其中 环区最小长度为人为设定的Rmin ,而 环区最大长度是当茎区长度取得最小值Smin时的环区长度l-2*Smin
- i表示DNA序列起始处的索引,其中i最小从1处开始,最大可以到l-2s-r处,其中s和r皆为前两步中确定的值。
不同文章中发卡结构约束的定义及区别
- 上一章中定义此处标记为 [*]定义 而与其他定义相区别,其他定义则根据其引用的参考文献进行标记,即若此处定义出自于参考文献[1],则将其标记为 [1]定义
[2]定义

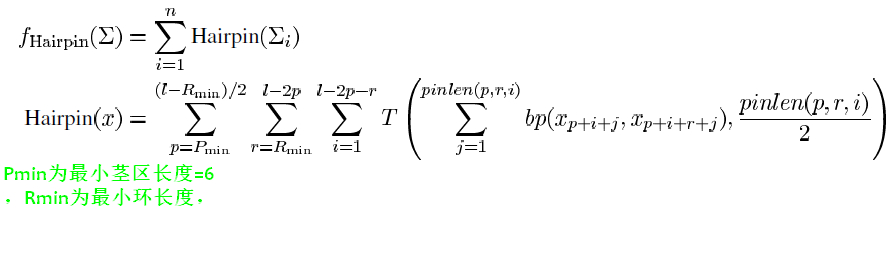
- 这个pinlen(p,r,i)很奇怪,定义为当假结中心在(p+i+r/2)时,可能的最大的茎区配对可能数 , 在作者2008发表的文章[3]中指出pinlen即为当前假定
的茎区数。 - 但是\(x_{p+i+j}和x_{p+i+r+j}的位置并不是假结茎区中一一对应的,[ * ]定义中是一一对应的关系\)
[3]定义
- 在S.Y.Shin于2008年发表的[3]文章中,提出了如下定义:
![]()
- [3] 定义与 [ * ]定义差别在于 [3] 定义中茎区匹配索引比 [ * ] 中均索引大1.
[4]定义
- 在S.Y.Shin于2002年发表的[4]文章中,提出了如下定义:
![]()
- 其中Hairpin(x,c)函数没有明确的数学定义。仅仅是给出一个概念。
[5]定义
-
\[\operatorname { Hairpin } ( x ) = \sum _ { s = S _ { \min } } ^ { \left( l - R _ { \mathrm { min } } \right) / 2 } \sum _ { r = R _ { \min } } ^ { l - 2 s } \sum _ { i = 1 } ^ { l - 2 s - r } T \left( \sum _ { j = 1 } ^ { s } b p \left( x _ { s + i - j } , x _ { s + i + r + j } \right) , \frac { S } { 2 } \right) \]
- 与[ * ]的区别在于\(x _ { s + i - j } , x _ { s + i + r + j }[5],x _ { s + i - j } , x _ { s + i + r + j-1 }[ * ]\)
分析与比较
可以看出[ * ]中Hairpin的计算公式较为正确
| No | J index | Expression x | Expression y |
|---|---|---|---|
| * | - | \(x _ { s + i - j}\) | \(x _ { s + i + r + j-1}\) |
| - | j=1 | \(x_{s+i-1}\) | \(x_{s+i+r}\) |
| - | j=s | \(x _ {i}\) | \(x _ { i + r + 2s-1}\) |
| 2 | - | \(x_{s+i+j}\) | \(x_{s+i+r+j}\) |
| - | j=1 | \(x_{s+i+1}\) | \(x_{s+i+r+1}\) |
| - | j=s | \(x_{i+2s}\) | \(x_{i+r+2s}\) |
| 3 | - | \(x _ { s + i - j+1}\) | \(x _ { s + i + r + j}\) |
| - | j=1 | \(x_{s+i}\) | \(x_{s+i+r+1}\) |
| - | j=s | \(x _ {i+1}\) | \(x _ { i + r + 2s}\) |
| 5 | - | \(x _ { s + i - j}\) | \(x _ { s + i + r + j}\) |
| - | j=1 | \(x_{s+i-1}\) | \(x_{s+i+r=1}\) |
| - | j=s | \(x _ {i}\) | \(x _ { i + r + 2s}\) |





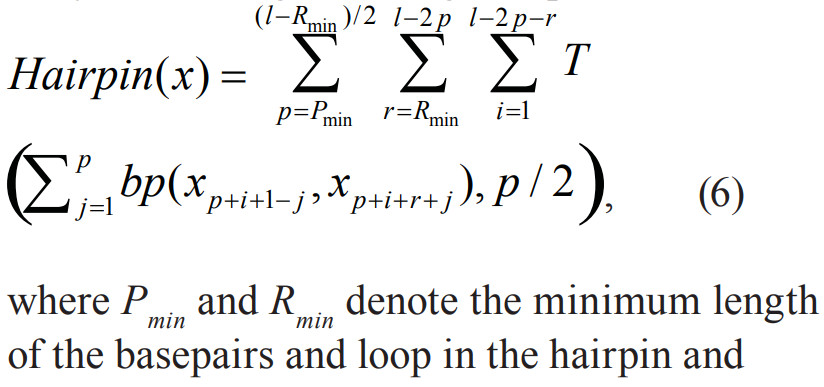


 浙公网安备 33010602011771号
浙公网安备 33010602011771号