网络流略解
今天牙齿痛得不行,去看了牙医,牙医医术高明,告诉我你的确有病但你先别急,明天再来还推荐了如果太痛了布洛芬疗法并叮嘱一天只能吃两粒,但我觉得吃了和没吃对学习上效果一样就没吃。于是我今天想必是做不了题了,来更博客。
网络最大流
最大流问题是网络流的基础,他代表着一类反悔贪心的模板。
定义
现在我们把自来水厂连到你家的管道想象成一个有向无环图,我们把自来水厂作为源点,把你家作为汇点。管子不是万能的,每个管子最多只能流过 \(w_i\) 的水流。此外,我们根据生活常识对每个中转点进行如下定义:
除了源点和汇点,图上的每个点流入和流出的流量是相同的。
我们把这个东西叫做流量平衡。举个例子,当存在 \(flow(u, v) = 3\),且 \(flow(v, w)=2\) 时,从 \(u\) 流到 \(v\) 的流量只能是 \(2\)。因为如果为 \(3\) 的话 \(flow(v, w)\) 这个管道受不了。
我们把每个管道还能容纳的流量称作一条边的剩余流量。举例,上一段中 \(flow(u, v)\) 的剩余流量为 \(1\)。
有了流量平衡,我们可以给最大流下定义:最大流是在满足流量平衡的条件下,你家能接到了最大流量。
错解
容易想到一个贪心:每次找一条路径,满足路径上的边剩余流量均为正(有一条边为 \(0\) 的话没有意义,因为此时这条路径对答案不产生贡献)。此时这条路径的贡献即为路径上的边权最小值。为了更新剩余流量,我们还要将路径上的所有边权都减去所贡献的答案。
我们把这样的路径叫做增广路。显然网络流就是由若干条增广路(可以重叠)组成的。
这个贪心是错误的。下面就是贪心的反例:
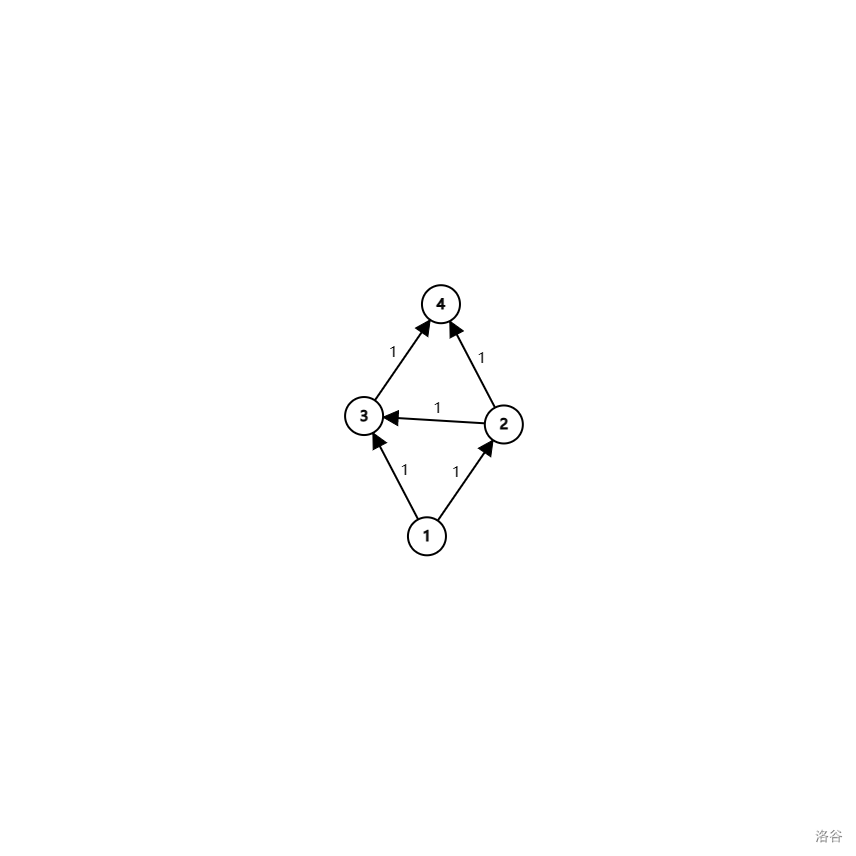
我们令 \(1\) 为源点,\(4\) 为汇点。如果我们的路径选择 \(1,2,3,4\),那么最大流量只有 \(1\),但是如果我们选择 \(1,3,4\) 与 \(1,2,4\),那么最大流量就有 \(2\) 了。
问题在于,这两种流法都是符合我们的做法的。对于两种策略,我们没办法事先知道哪个对。
改正
上面的做法不禁让我们想到:是不是我们的程序只要能自动判断走完一条增广路后,另一条增广路有可能更优不久行了吗?
于是我们利用反悔贪心的思想,对于每一条单向管道建立反向边,初始时反向边为 \(0\),当我们把正向边边权减少时,将反向边边权加上同样的值。这样,如果我们再选择反向边,就相当于没有选择这条边。由此达到了反悔的效果。
这种做法具有正确性了,我们把 dfs 实现的这种算法叫做 FF 算法,我们把用 bfs 实现的这种做法叫做 EK 算法。
为什么要用 bfs 实现呢?因为这样可以使每次找到的增广路为最短,最大时间复杂度就与玄学的流大小无关了。但这并不是说 dfs 时间复杂度就略逊一筹,换句话说,只要题目规定了很小的边权,那么 dfs 可能还会更快。具体可以参见 CF1318F。
也许你已经看出来了,这种做法常数很大!为了达到最优的效果,我们要尝试优化。
优化
优化后的算法包含两个部分,分层图优化和当前弧优化。
我们发现一条增广路一条增广路的找太慢了,为什么不找完一条后一个个退回上面的点继续寻找呢?
但同时,我们又想保留 bfs 寻找最短增广路的性质来保证复杂度上界。因此我们以 bfs 的层数作为依据进行 dfs 增广,以达到合并重复增广路的效果。
当前弧优化显得更为简单:在增广完一条边后,在这次增广中,我们不可能再用这条边的流量了。因此我们不断更新每个点链式前向星起点,进一步避免搜索到无用状态。
这样就变成了 OI 界公认的网络流算法 dinic 了。时间复杂度上界为 \(O(v^2e)\)。在题目中,最大流不卡 dinic 就像字符串不卡双哈希一样成为了公认的常识(真的是这样的吗?)。当然也需要注意,如果题目里给了你边权小于 \(25\) 这种不明不白的范围,请立刻写 FF 算法。因为这样的复杂度与边权相关。
用在二分图里的网络流复杂度为 \(O(v\sqrt{e})\),可以看出优于二分图匹配。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 5e5 + 5, INF = 5e13;
template<typename T> bool chkmax(T &a, T b) { return a < b ? (a = b, 1) : 0; }
template<typename T> bool chkmin(T &a, T b) { return a > b ? (a = b, 1) : 0; }
template<typename T> T read() { T a;cin >> a;return a; }
int n, m;
template<const int M>
struct graph {
int st[M], nx[M << 1], to[M << 1], cur[M], cnt = 1;
ll val[M << 1];
void add(int u, int v, int w) { to[++cnt] = v;val[cnt] = w;nx[cnt] = st[u];st[u] = cnt; }
};
#define go(g, u, v, w) for (ll i = g.cur[u], v = g.to[i], w = g.val[i]; i; i = g.nx[i], v = g.to[i], w = g.val[i])
namespace Graph {
graph<N> g;
void add(int u, int v, int w) { g.add(u, v, w); }
int lev[N];
bool bfs(int s, int t) {//对图分层
memset(lev, -1, sizeof(lev));lev[s] = 0;
memcpy(g.cur, g.st, sizeof(g.st));
queue<int> q;q.push(s);
while (!q.empty()) {
int u = q.front();q.pop();
go(g, u, v, w) if (w > 0 && lev[v] == -1)
lev[v] = lev[u] + 1, q.push(v);
}
return lev[t] != -1;
}
ll dfs(int u, ll flow, int t) {
if (u == t) return flow;
ll res = flow;
go(g, u, v, w) {
g.cur[u] = i;//当前弧优化
if (w > 0 && lev[v] == lev[u] + 1) {
int c = dfs(v, min(w, res), t);res -= c;
g.val[i] -= c;g.val[i ^ 1] += c;
}
}
return flow - res;
}
ll dinic(int s, int t) {
ll ans = 0;
while (bfs(s, t)) {
ll p = dfs(s, INF, t);
ans += p;
}
return ans;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int s, t;
cin >> n >> m >> s >> t;
for (int i = 1, u, v, w; i <= m; ++i) {
cin >> u >> v >> w;
Graph::add(u, v, w);
Graph::add(v, u, 0);
}
cout << Graph::dinic(s, t);
return 0;
}
网络最小割
网络最小割是与最大流相对的概念,最小割是一个边集,当删去边集中的边后,源点和汇点不连通,且边集的流量和最小。
下面是网络流中最简明优雅的性质,它凭一句之力解决了最小割问题:
最小割等于最大流
可以这么理解:每一条增广路都是对流量做加法,而割实际上就是对流量做减法。因此,我们要把每一条增广路都割一刀,这样就没有任何加法给流量作贡献了。而割的是哪些边呢?根据贪心的思想,我们割的是作为增广路里流量最少的那条边。而这条边的流量刚好等于这条增广路贡献的流量。因此割出的最小流量就等于最大流。
有人可能就会要问了:那我如果两次割了同一条边不就算重了吗?对此的证明是:如果一条边作为了最小边,那它的所有流量肯定都在这条增广路上流满了(否则流量就还能增大)。那么另一条增广路里最小边就是 \(0\),这是不符合我们对增广路的定义的。因此不会出现这种情况。
这一部分的参考:
知乎 Pecco 算法学习笔记(28):网络流:https://zhuanlan.zhihu.com/p/122375531


