点分治与点分树
点分治和点分树真的是各种意义上的好东西。不仅好玩,而且写完一看自己的代码5.几kb:“wc我今天搞了好多学习”。
在做关于树的题时,我们会遇到一类题型:题目跟路径有关,你找到两个点当端点求贡献,然后你发现这两个点当形成路径跨过根时,相比没跨过根,求贡献的方法不一样。
详情可参考洛谷模板题:点分治1
给定一棵有 \(n\) 个点的树,询问树上距离为 \(k\) 的点对是否存在。
在这道题中,没跨过根的路径要减去 LCA 的深度,跨过根的路径只要把深度一加就好了。后者显然比前者简单许多。
鲁迅说过:“偷懒是人类第一生产力”。在面对即将进行的宏大的分类讨论时,我们往往会选择回避掉这个问题。例如:换一个根,把原来与根的关系破坏掉。
很赞的一点是由于路径换根后不变,所以换一个根实际上不影响答案。
我们确定了算法的目的:我们要让每条路径都有一个“根”供其跨越与计算答案。那么我们试着写出算法的步骤
1:找到一个根
2:统计跨过根的路径的答案
3:递归处理哪些路径没跨过根
4:找到一个新根,回到第二步
算法的雏形有了,我们还需要处理几个问题:
1:到底哪些路径没跨过根?
两端点 LCA 等于根的路径都跨过了根,剩下的东西都是没跨过根的。画个图就知道他们的两端点属于根的同一子树。
这也意味着我们在处理完根以后,我们要处理的是根的每一个子树,并在每一个子树中选出一个新根。
2:选出新根后要遍历哪些节点?
根据问题 1 可以得知:只需要遍历老根的这个子树的节点就行了,如果你选一个子树内的点,选一个子树外的点组成路径,那么就跨过了根。如果你选了两个子树外的点且他们属于同一子树,那么就是其他新根的任务了。
发现这一套:选中间点→处理能处理的问题→划分子结构→选中间点 的步骤就是分治。这也是算法名字的由来。
3:这算法时间复杂度行不行?
我们发现一件事情:划分出的子树大小越小,算法所需时间越少。例如下图:

以 1 为根的划分,需要的划分次数比以 2 为根要少。因为划分时留下的没跨过根节点的路径越少。
怎么让划分出的子树大小最小?这是个经典且简单的问题,答案就是选重心。
以重心为根,每个子树的大小每次变为原来的 1/2。总共最多划分 \(log(n)\) 层,子树最多的一层最多有 \(n\) 个子树(每棵子树大小为 1)。总复杂度为 O(nlogn)。实际上由于我们还要对每个子树求重心,所以为 \(O(nlog^2n)\)
4:怎么统计跨过根的答案?
一般我们三种不同的方法:
第一种做法:我们可以先不管子树的性质,只管满足条件,然后再单独统计这个子树内部与内部的答案,容斥一下就好了。
第二种做法:给每个子树染个不同的颜色,统计颜色不同的答案。
第三种做法:在遍历子树时,我们先遍历,再求答案,再更新,这样可以保证每棵子树只会与前面的子树求答案。
以上题为例:
这道题说白了我们只要找出一条满足条件的路径就行,最简单的办法就是染色后把当前根管的点按深度排个序,让两个指针一个指头一个指尾,不断向中间靠近,直到两指针对应的深度之和等于 \(k\) 。如果此时颜色相同还要继续跳(优先选择跳完后深度不变的那一边)。
for(int i = 1;i <= m;i ++)
{
int l = 1, r = tot;
if(pd[i])
continue;
while(l < r)
{
if(dep[h[l]] + dep[h[r]] > que[i])
r --;
else if(dep[h[l]] + dep[h[r]] < que[i])
l ++;
else if(col[h[l]] == col[h[r]])
{
if(dep[h[r]] == dep[h[r - 1]])
r --;
else
l ++;
}
else
{
pd[i] = 1;
break;
}
}
}
处理完这四个问题,点分治的算法过程已经完成了。时间复杂度为 \(O(nlog^2n+nmlogn)\)。其中前面为分治复杂度,后面为处理询问复杂度。
推荐习题:
现在我们对于树上路径问题能够使用点分治解决了,但我们发现如果带上修改我们就得每次修改后再做一次点分治,复杂度就上去了。
例如模板点分树
在一片土地上有 \(n\) 个城市,通过 \(n-1\) 条无向边互相连接,形成一棵树的结构,相邻两个城市的距离为 \(1\),其中第 \(i\) 个城市的价值为 \(value_i\)。
不幸的是,这片土地常常发生地震,并且随着时代的发展,城市的价值也往往会发生变动。
接下来你需要在线处理 \(m\) 次操作:
0 x k表示发生了一次地震,震中城市为 \(x\),影响范围为 \(k\),所有与 \(x\) 距离不超过 \(k\) 的城市都将受到影响,该次地震造成的经济损失为所有受影响城市的价值和。
1 x y表示第 \(x\) 个城市的价值变成了 \(y\) 。为了体现程序的在线性,操作中的 \(x\)、\(y\)、\(k\) 都需要异或你程序上一次的输出来解密,如果之前没有输出,则默认上一次的输出为 \(0\) 。
虽然每次的值会更改,但我们点分治经过的点的顺序是不变的,因为树的形态不变。那么我们是不是可以提前把点分治要走的点存好,然后在上面修改呢?
如果我们把根同每个子树的重心连接起来,就会发现最终这也形成了一棵树。
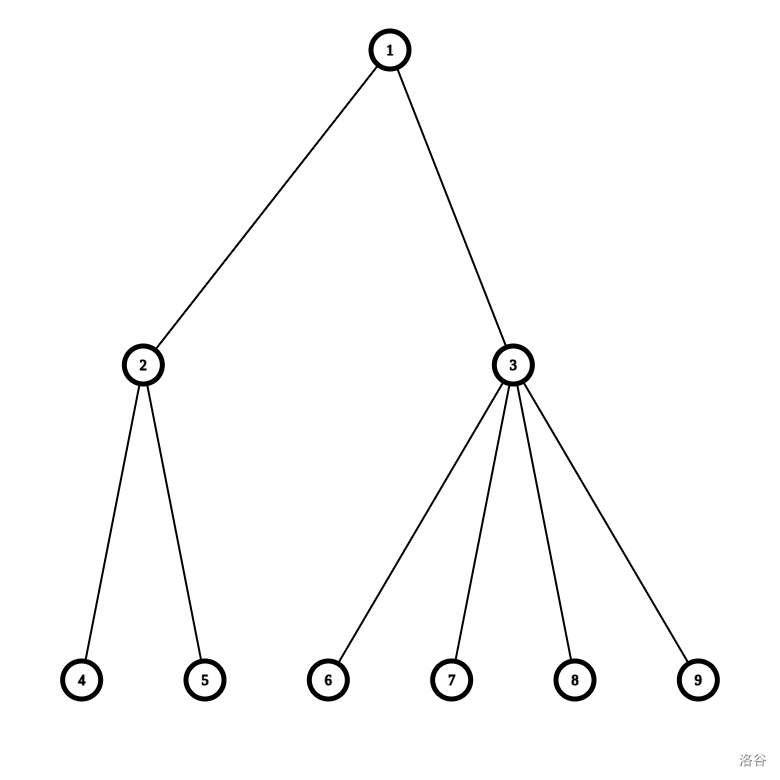
变为了:
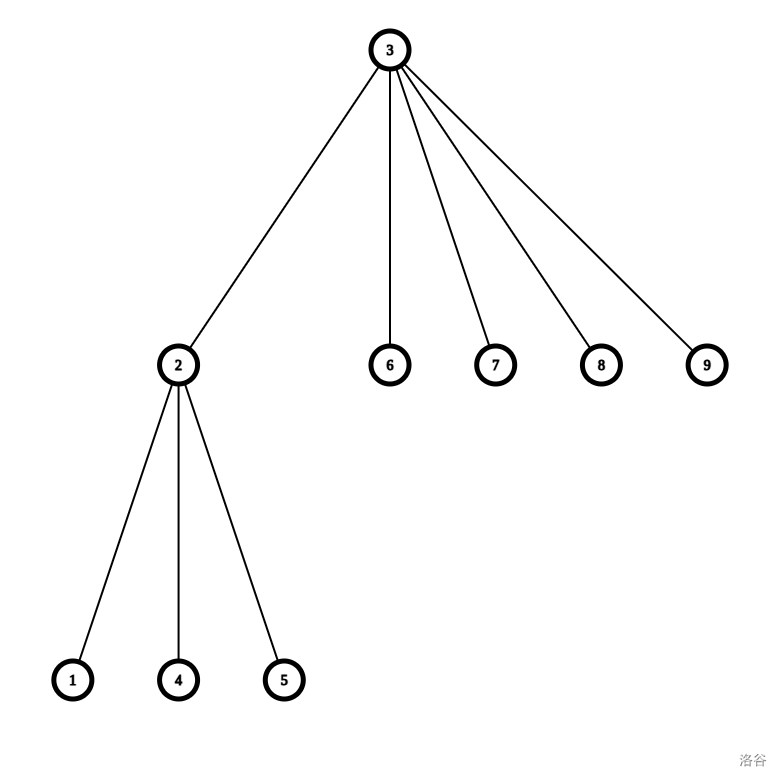
这个树跟原树有联系,每个点的子树就是点分治时以这个点为根管的节点。但好像不是那么有联系。我们甚至不能看出两个点之间的路径关系。
这个树有个可爱的性质,这是根据点分治的递归关系建出来的,点分治最多递归 \(logn\) 次,这个树最高就是 \(logn\) 层。如果我们把这棵树所有子树大小相加,也只是 \(nlogn\) 级别的。
最后一句话如果不理解,可以算算贡献,每一个点的贡献就是她的深度,最多 \(logn\),所以 \(n\) 个点就是 \(nlogn\)。
这样的话,一些常规可能卡空间的做法:例如每个子树动态开点建线段树,也变得可行了起来。
继续观察,根据点分治的过程,这棵树的不同子树在原树中也属于不同子树。那么我们就找到了一个中转点:这个树上的两点 \(u,v\) 的 LCA 必定在原树从 \(u\) 到 \(v\) 的路径上。因为 \(u\) 和 \(v\) 在原树上属于 LCA 的不同子树。
总结一下两条性质:
- 点分树最高 \(logn\) 层。如果我们把树所有子树大小相加,总和为 \(nlogn\) 级别。
- 这个树上的两点 \(u,v\) 的 LCA 必定在原树从 \(u\) 到 \(v\) 的路径上。
为了表示方便,我们设点分树上 \(u\) 和 \(v\) 的 LCA 为 \(l\),原树上为 \(lca\)。
根据性质 2,我们可以把两点的距离 \(dis(u, v)\) 变为 \(dis(u,l)+dis(v,l)\)。
询问为我们固定了节点 \(u\) 与距离 \(k\),我们只需求出对于 \(u\) 及 \(u\) 的祖先 \(z\),\(dis = k - dis(u,z)\) 的点点权之和为多少就行了。这个可以用动态开点线段树解决,将距离作为下标,将价值作为权值即可。
那么对于询问的节点 \(u\) ,我们统计她自身子树中的答案,然后暴力一个个往上跳,依次统计即可。
等等,好像有问题。在跳到父亲 \(fa\) 后, \(u\) 及其子树有可能会被算到第二遍。要减去才行。
怎么减呢?我们要的是减去 \(u\) 子树中与 \(fa\) 距离 \(k - dis(u, fa)\) 的点的点权,很 naive 的想法是减去 \(u\) 子树中与 \(u\) 距离 \(k - dis(u,fa) - 1\) 的点的点权。点分树上的距离和原树没有一点关系,所以这个 \(k - dis(u, fa) - 1\) 中的 \(1\) 意义不明。
所以我们忽略点分树中的距离关系,直接用另一棵动态开点线段树求解。
再次强调点分树上的距离没有任何意义,所以如果祖先的距离超过了 \(k\) 只要忽略当前祖先,上面的祖先还是要进行统计的。
修改也是如此,我们修改完 \(u\) 本身后,暴力往上跳,依次进行修改即可。
#include <bits/stdc++.h>
#define ll long long
#define For(i,a,b) for( int i=(a); i<=(b); ++i)
#define Rep(i,a,b) for( int i=(a); i>=(b); --i)
using namespace std;
void init()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
}
const int maxn = 100105;
int n, m;
int a[maxn];
int root;
vector<int> e[maxn], t[maxn];
bool vis[maxn];
int rt, mx[maxn], si[maxn], trTot, dfn[maxn], dep[maxn], num[maxn << 1];
int st[maxn << 1][23], f[maxn];
// find LCA
void findDeep(int u, int fa)
{
dfn[u] = ++ trTot;
num[trTot] = u;
for(auto v : e[u])
{
if(v == fa) continue;
f[v] = f[u];
dep[v] = dep[u] + 1;
findDeep(v, u);
num[++ trTot] = u;
}
}
void ST()
{
memset(st, 0x3f, sizeof(st));
for(int i = 1;i <= trTot;i ++)
st[i][0] = num[i];
for(int j = 1;j <= 20;j ++)
for(int i = 1;i + (1 << j) <= trTot;i ++)
{
if(dep[st[i][j - 1]] < dep[st[i + (1 << (j - 1))][j - 1]])
st[i][j] = st[i][j - 1];
else
st[i][j] = st[i + (1 << (j - 1))][j - 1];
}
}
int LCA(int u, int v)
{
if(dfn[u] > dfn[v])
swap(u,v);
int l1 = dfn[u],l2 = dfn[v];
int len=log2(l2 - l1 + 1);
if(dep[st[l1][len]] < dep[st[l2-(1 << len) + 1][len]])
return st[l1][len];
else
return st[l2 - (1 << len) + 1][len];
}
int dis(int u, int v)
{
return dep[u] + dep[v] - (2 * dep[LCA(u, v)]);
}
// find zhong
int Tot;
void findRt(int u, int fa)
{
mx[u] = 0;
si[u] = 1;
for(auto v : e[u])
{
if(vis[v] || v == fa)
continue;
findRt(v, u);
si[u] += si[v];
if(si[v] > mx[u]) mx[u] = si[v];
}
mx[u] = max(mx[u], Tot - si[u]);
if(mx[rt] > mx[u]) rt = u;
}
void build(int u)
{
vis[u] = 1;
for(auto v : e[u])
{
if(vis[v] == 1)
continue;
rt = 0;
Tot = si[v];
findRt(v, u);
t[u].push_back(rt);
t[rt].push_back(u);
build(rt);
}
}
void read()
{
cin >> n >> m;
int u, v;
for(int i = 1;i <= n;i ++) cin >> a[i];
For(i, 1, n - 1)
{
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
}
struct linetree
{
int tot, rt[maxn];
struct point
{
int val, ls, rs;
}tr[5000006];
void push_up(int u)
{
tr[u].val = tr[tr[u].ls].val + tr[tr[u].rs].val;
}
void ins(int &p, int l, int r, int fl, int k)
{
if(l > fl || r < fl)
return ;
if(p == 0)
p = ++ tot;
if(l == r)
{
tr[p].val += k;
return ;
}
int mid = l + r >> 1;
ins(tr[p].ls, l, mid, fl, k);
ins(tr[p].rs, mid + 1, r, fl, k);
push_up(p);
}
int query(int p, int l, int r, int fl, int fr)
{
if(l > fr || r < fl || p == 0)
return 0;
if(l >= fl && r <= fr)
return tr[p].val;
int mid = l + r >> 1, ans = 0;
ans += query(tr[p].ls, l, mid, fl, fr);
ans += query(tr[p].rs, mid + 1, r, fl, fr);
return ans;
}
}zi, fu;//zi 以距离当前点的距离为下标,fu 以距离当前点父亲的距离为下标
void Build()
{
rt = 0;
mx[0] = 2147483647;
findDeep(1, -1);
ST();
Tot = n;
findRt(1, -1);
root = rt;
build(rt);
}
int fa[maxn];
void dfs(int u, int f)
{
for(auto v : t[u])
{
if(v == f) continue;
fa[v] = u;
dfs(v, u);
}
}
void change(int u, int k, int r)
{
if(u == 0) return ;
zi.ins(zi.rt[u], 0, n, dis(r, u), k);
if(fa[u])
fu.ins(fu.rt[u], 0, n, dis(r, fa[u]), k);
change(fa[u], k, r);
}
void chu()
{
for(int i = 1;i <= n;i ++)
change(i, a[i], i);
}
int jump(int u, int fr, int k, int from)
{
if(u == 0) return 0;
if(dis(u, fr) > k) return jump(fa[u], fr, k, u);
int nope = (from == 0 ? 0 : fu.query(fu.rt[from], 0, n, 0, k - dis(u, fr)));
return zi.query(zi.rt[u], 0, n, 0, k - dis(u, fr)) + jump(fa[u], fr, k, u) - nope;
}
void que()
{
ll q, x, k, ans = 0;
For(_, 1, m)
{
cin >> q >> x >> k;
x ^= ans;k ^= ans;
if(q == 0)
{
ans = jump(x, x, k, 0);
cout << ans << endl;
}
else
{
change(x, k-a[x], x);
a[x] = k;
}
}
}
int main()
{
init();
read();
Build();
dfs(root, -1);
chu();
que();
return 0;
}
推荐习题:
洛谷上有题单。


