[ARC152D] Halftree题解
-
很好的一道题,即使是我这种菜鸡也感到心潮澎湃。
-
直觉有余,证明不足。思路有余,推导不足。
-
无论是什么比赛,对拍都是最有效的查错方式。
-
本篇题解里的所有图片采用 graph_editor 制作。
题意简述
给你一张没有边的,\(n\) 个点的图,点的编号从 \(0\) 到 \(n-1\),再给你一个参数 \(k\)。你可以执行以下操作任意次:
- 选择点 \(u\) 和点 \(v\),将其连边,并且将 \((u+k) \mod n\) 与 \((v+k) \mod n\) 连边。
你需要在第一行输出你的操作次数 \(m\),在第 \(2\) 到 \(m+1\) 行输出你每次操作选择的 \(u\) 和 \(v\),使得经过你的操作,这张图变为无重边,无自环的一棵树。
思路整理
在以下的推导中,我们设 \(to_i=(i+k) \mod n\),\(p=gcd(n,k)\)。
你发现,如果 \(n\) 为偶数,必然无解。因为每次加入两条边,不可能产生奇数条边。
对于奇数,你想到了这样一种形式:将 \(0\) 和 \(to_0\) 连边,这时 \(to_0\) 会与 \(to_{to_0}\) 连边。之后将每个点 \(u\) 与 \(0\) 连边,此时 \(to_u\) 会与 \(to_0\) 连边。每次新加两个点,一开始有三个点。这样加下去总能满足条件。这看上去很对,你很高兴,认为今天能上大分。
显然电脑很不高兴,她给你这样一组数据:\(n=15,k=6\)。
你把图画出来,发现有一丝不对劲:
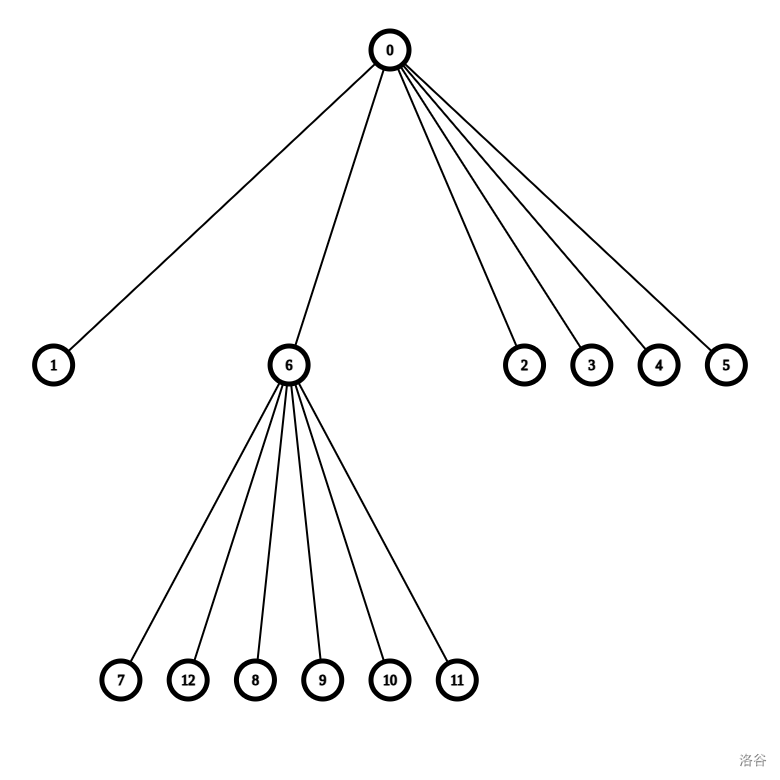
少了两个点!\(13\) 本来要和 \(7\) 对 \(0\) 和 \(1\) 连边,但 \(7\) 被 \(5\) 抢了!
你转念一想:我直接让 \(5\) 跟 \(7\) 连边,那么 \(13\) 就会与 \(7\) 连边。问题似乎被解决了!
然后你造出来了 \(p\) 条链。

你很不高兴,决定将这 \(p\) 条链连起来。
你试着将 \(0\) 和 \(1\) 连起来,发现 \(to_0\) 和 \(to_1\) 也连了起来。这就是个环了,于是你决定将 \(1\) 所在的那条链全断开。
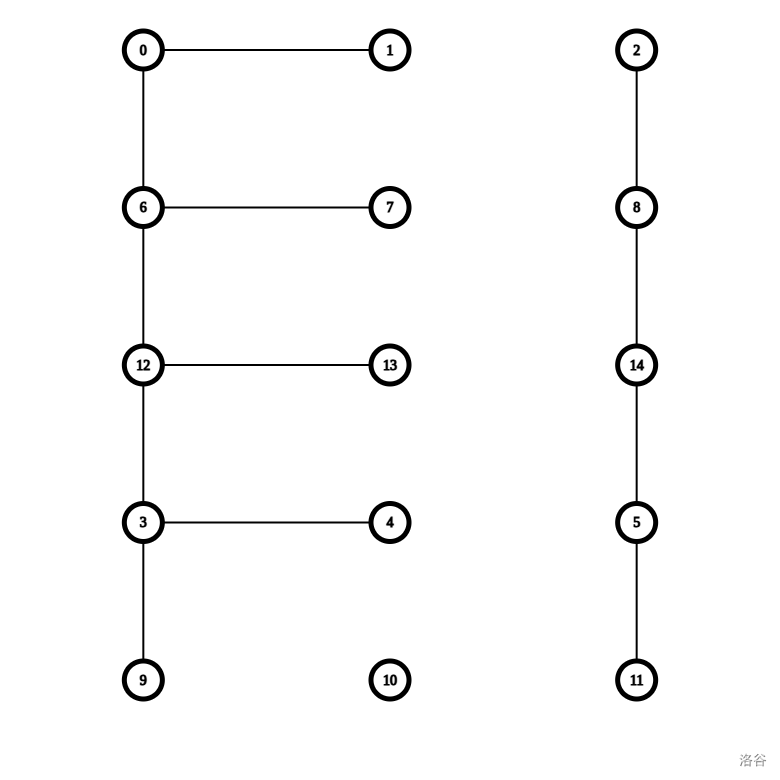
这种方案有两个问题:
- 最后一行没人管
- 最后一列没人管
你试图将两个没人管的东西连起来: \(10\) 和 \(11\),然后会连上 \(1\) 和 \(2\)。。。成了!
如果有更多列呢?那就多做几遍!
这里提供一份 \(n=35,k=7\) 的答案图。
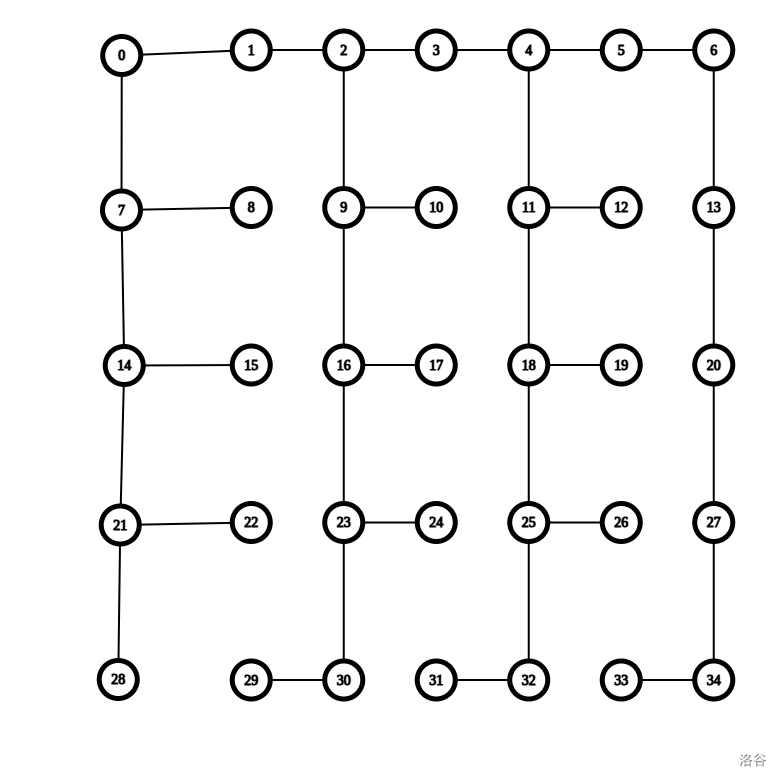
作为一个精益求精的人,你想要证明当 \(n\) 为奇数时都能构造出上面的树。
你发现,构造出这个树的条件为每条链的节点数为奇数,且有奇数条链。
显然,当 \(n\) 为奇数时 \(p\) 为奇数。第一条链的节点集合 \(S\) 为 \(0,p,2p,...,(n/p-1)*p\)。总共 \(n/p\) 个点。奇数被奇数整除得奇数
所以,第 \(i\) 条链可以表示为 \(0+(i-1),p+(i-1),...(n/p-1)+(i-1)\)。起点从 \(0\) 到 \(p-1\) 都有可能,所以总共有 \(p\) 条链。为奇数。
你很高兴,上了大分。因为这一场有许多人都被小学追及问题难住了。
代码很短,不给代码。

