[题解]涂色

涂色-弱

题面

小 Y 正用图章和颜料在草稿纸上乱涂颜色。对于数学敏感的他，突然发现这是一个有意思的数学问题：给出有 N 个格子的纸、宽度为 K 个格子的图章和 M 种不同的颜色，每次用图章把纸上连续的 K 个格子上染任意一种颜色，最后把纸涂满，那么小 Y 想知道最后纸上的颜色序列有多少种不同的情况？（对于 100%的数据 N,M,K≤10 000 000）

解题思路

​ 首先我们通过思考可以得出这样的结论，最后的纸上至少会有一个长度为k的颜色相同的色块，除了这个色块以外其他的色块我们是可以想办法，所以我们可以考虑用总的方案数减去不合法的方案（此处不合法的为没有长度为k的颜色相同的色块的方案）。

​ 那么我们可以开始思考如何求出不合法的方案。记f[i]为涂到第i个格子后一共出现的不合法方案的个数。

​ 对于纸条上的第i个格子，我们大致有两种选择，即选择与前一个方块的颜色不同或相同。对于不同，如图
则因为有m种颜色，所以f[i]+=f[i-1](m-1)，因为他不会对前面的结果造成影响。

​ 对于相同，那么再考虑i-1与i-2不同

所以再加上f[i-2](m-1)，以此类推，则我们得到一个方程

\[f[i]=\sum^{i-1}_{j=i-k+1}f[j] \]

化简得\(f[i]=m*f[i-1]-(m-1)f[i-k]\)

但这个并不适用于所有的情况，当i<k时，随便上色都不会出现不合法的方案,所以得到第二个方程

\[f[i]=m*f[i-1](i<k) \]

然后很明显的，这个式子到了k，就会出现不合法的情况，而相当于前k个全排列，不合法的情况就会有m种。

\[f[k]=m*f[k-1]-m \]

之后的就可以使用第一个方程计算。而总方案相当于是全排列，使用快速幂就好。

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll MAXN=10000000,mod=1000000007;
ll n,m,k,a[MAXN];
ll ans;
ll KSM(ll a,ll b,ll mod){
	ll p=1;
	while(b){
		if(b&1)p*=a;
		b>>=1;
		p%=mod;
		a=a*a;
		a%=mod;	
	}
	return p;
}
int main(){
	cin>>n>>m>>k;
	a[0]=1;
	for(int i=1;i<=n;++i){
		if(i<k)a[i]=m*a[i-1]%mod;
		else if(i==k)a[k]=(m*a[i-1]-m+mod)%mod;
		else a[i]=(m*a[i-1]-(m-1)*a[i-k]+mod)%mod;
	}
	cout<<(KSM(m,n,mod)-a[n]+mod)%mod;
}

涂色-强

题面

​ 数据范围上调至n<=2^31-1,m<=105，k<=100。

思路

​ 由于数据加强了，\(O(n)\)的复杂度就会超时，那么此时我们需要想出一个方法解决这道题。

​ 很显然的当数据加强了之后，这个简化后的方程就不能用了。但是很明显的K的值变小了，于是我们就还是可以算出前k个值，（空间问题是可以用滚动来解决的，但是数据加强主要是卡时间）。那么我们看回未化简前的式子

\[f[i]=\sum^{i-1}_{j=i-k+1}f[j] \]

它是一个连乘的东西，而我们已经算出了前k项。乘法想要加快速度，我们使用矩阵加速。

​ 具体的来说，我们已经有了一个只有一行的矩阵：\(f[1],f[2],f[3]...f[k]\),如果说我们可以乘上一个固定的矩阵，我们能乘出一个带有\(f[k+1]\)的有序单行矩阵，就很nice。然后我们回到式子，很显然的，与\(f[k+1]\)有关的为\(f[k],f[k-1]...f[2],(k+1-k+1=2)\),所以说我们的初始矩阵是\(f[k]...f[2]\),很显然的长度为k-1，然后我们思考着怎么样来算出\(f[k+1]\),由上面的公式得出，需要将初始矩阵的每一项乘\((m-1)\)求和。

​ 对吧，有乘，有和，不用矩阵乘法你用什么。有了上面的讨论，我们得出固定的矩阵的第一列均为\(m-1\)（由于矩阵乘法的计算方式），然后我们想要保证之后乘出的矩阵大小不变，所以固定矩阵的大小为\((k-1)*(k-1)\),然后为了保证统一性，后面的乘法达到的目的是向下移，如图。

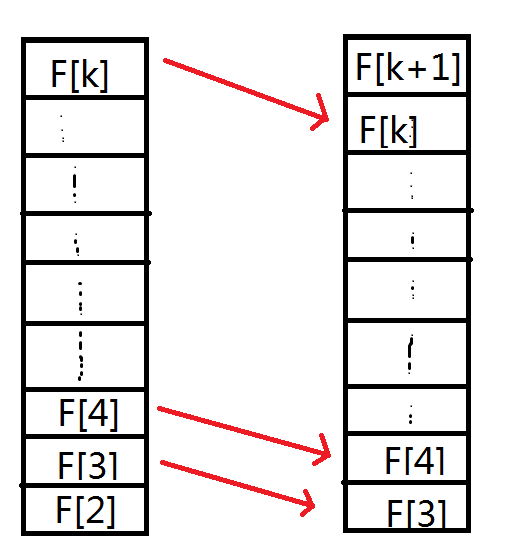
（但是实际上左边那个是横着的就对了），再根据矩阵乘法的乘法法则，固定矩阵大概长这样。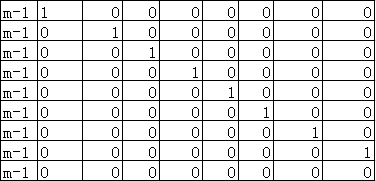

就这样，然后模拟一套带走就行（打得我脑阔痛）

Code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll MAXN=10000000,mod=1000000007;
ll n,m,k;
ll KSM(ll a,ll b,ll mod){
	ll p=1;
	while(b){
		if(b&1)p*=a;
		b>>=1;
		p%=mod;
		a=a*a;
		a%=mod;	
	}
	return p;
}
ll dwjz[105][105],a[105],ans[105],f[105],res[105][105],c[105][105];
void zjksm(int b){
	for(int i=1;i<=k-1;++i)res[i][i]=1;
	while(b){
		if(b&1){
			memset(c,0,sizeof(c));
			for(int i=1;i<=k-1;++i)
				for(int j=1;j<=k-1;++j)
					for(int q=1;q<=k-1;++q)
						c[i][j]=(c[i][j]+res[i][q]*dwjz[q][j])%mod;
			for(int i=1;i<=k-1;++i)
				for(int j=1;j<=k-1;++j)res[i][j]=c[i][j];
		}
		b>>=1;
		memset(c,0,sizeof(c));
		for(int i=1;i<=k-1;i++)
			for(int j=1;j<=k-1;++j)
				for(int q=1;q<=k-1;++q)
					c[i][j]=(c[i][j]+dwjz[i][q]*dwjz[q][j])%mod;
		for(int i=1;i<=k-1;++i)
			for(int j=1;j<=k-1;++j)dwjz[i][j]=c[i][j];
	}
}
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=k-1;++i)dwjz[i][1]=m-1;
	for(int i=1;i<=k;++i)dwjz[i][i+1]=1;
	f[0]=1;
	for(int i=1;i<=k;++i){
		if(i<k)f[i]=m*f[i-1]%mod;
		else if(i==k)f[k]=(m*f[i-1]-m+mod)%mod;
	}
	for(int i=1;i<=k-1;++i)a[i]=f[k+1-i];
	zjksm(n-k);
	ll u=0;
	for(int i=1;i<=k-1;++i)u=(u+res[i][1]*a[i])%mod;
	cout<<(KSM(m,n,mod)-u+mod)%mod;
}