基于归并排序的算法题
小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组 的小和。
就是在 合并的时候,当左边数组的数小于右边数组的数的时候,就开始统计当前左边数组的小和。是当前右边数组个数*当前左边数组的值。
注意:当左右数组值相等的时候。必须是合并右树组的值。
package basicsort
import "fmt"
func Small_sum_ms(arr []int) int {
return process_ms(arr)
}
func process_ms(arr []int) int {
if len(arr) <= 1 {
return 0 //递归的终止条件。只有1个数,就是0
}
mid := len(arr) / 2
// 开辟俩个数组
l_arr := make([]int, len(arr[:mid]))
r_arr := make([]int, len(arr[mid:]))
copy(l_arr, arr[:mid])
copy(r_arr, arr[mid:])
// 递归调用俩个数组
l_res := process_ms(l_arr)
r_res := process_ms(r_arr)
fmt.Println(l_res, r_res)
l_index := 0
r_index := 0
c_index := 0
res := 0 // 小数累加和
for l_index < len(l_arr) && r_index < len(r_arr) {
if l_arr[l_index] < r_arr[r_index] {
//左数组的数 a 小于 右数组的数, a就是当前右树组所有数的小数,
// res += l_arr[l_index] * (len(r_arr) - r_index + 1) //开始计算错误的地方
res += l_arr[l_index] * (len(r_arr) - r_index)
arr[c_index] = l_arr[l_index]
l_index++
} else {
//右数组的数小或等于,直接合并。不需要计算
arr[c_index] = r_arr[r_index]
r_index++
}
// 数组越界。应该是if else。 不能if if 。l_index已经增1了。淦。。
// if l_arr[l_index] >= r_arr[r_index] {
// //右数组的数小或等于,直接合并。不需要计算
// arr[c_index] = r_arr[r_index]
// r_index++
// }
c_index++
}
// 当只有单个数组还有数据,不需要累加
for l_index < len(l_arr) {
arr[c_index] = l_arr[l_index]
c_index++
l_index++
}
for r_index < len(r_arr) {
arr[c_index] = r_arr[r_index]
c_index++
r_index++
}
//返回当前递归计算的结果,左数组的结果 + 右数组的结果 + 当前合并的结果
return res + l_res + r_res
}
逆序对问题
剑指 Offer 51. 数组中的逆序对
在一个数组中,左边的数如果比右边的数大,则这两个数构成一个逆序对,请打印所有逆序 对。
也就是在合并的时候,开始计算
func reversePairs(nums []int) int {
res := process(nums)
return res
}
func process(arr []int) int {
if len(arr) <= 1 {
return 0
}
mid := len(arr) / 2
l_arr := make([]int, len(arr[:mid]))
r_arr := make([]int, len(arr[mid:]))
copy(l_arr, arr[:mid])
copy(r_arr, arr[mid:])
l_res := process(l_arr)
r_res := process(r_arr)
l_i, r_i, c_i := 0, 0, 0
res := 0
for l_i < len(l_arr) && r_i < len(r_arr) {
if l_arr[l_i] <= r_arr[r_i] {
arr[c_i] = l_arr[l_i]
l_i ++
} else {
res += len(l_arr) - l_i
arr[c_i] = r_arr[r_i]
r_i ++
}
c_i ++
}
for l_i < len(l_arr) {
arr[c_i] = l_arr[l_i]
l_i++
c_i++
}
for r_i < len(r_arr) {
arr[c_i] = r_arr[r_i]
r_i++
c_i++
}
return l_res + r_res + res
}
快速排序
根据一个数,将一个数组分成左边全部小于等于num,右边全部大于num
less: 小于等于的区域。初始值 -1
i:当前要看的数的索引
1)当[i] <= num, [i] 和 [less + 1] 交换, i++, less ++ ,此处less + 1可能是大于num的数,也可能是自己和自己交换。
2) 当[i] > num, 只有i++, 再碰到 <= num的数,就和[less + 1] 交换了。
结束条件就是数组 循环看完一遍了。

func QucikSort01(arr []int, num int) {
less := -1 // 小于等于 num区域
for i := 0; i < len(arr); i++ {
// 如果当前数小于 等于 num
if arr[i] <= num {
swap(arr, less+1, i) //小于等于 区域右扩
less++
}
}
}
进阶,要分为三个区域,左边是小于 num, 中间是等于 num,右边是大于num
less: 小于num的区域,初始值-1
more: 大于num的区域,初始值len(arr)
i:当前遍历的索引
终止条件是i == more ,就是等于区域和大于区域碰着了
- 分三种情况
1)[i] < num, [less + 1] 和 [i] 交换,less ++, i++
2) [i] == num, i++
3) [i] > num, [more - 1] 和 [i] 交换,more --, i不动,因为 more-1还未看。

func QuickSort02(arr []int, num int) {
less := -1
more := len(arr)
i := 0
for i < more {
if arr[i] < num {
swap(arr, less+1, i)
less++
i++
} else if arr[i] == num {
i++
} else {
swap(arr, more-1, i)
more--
}
}
}
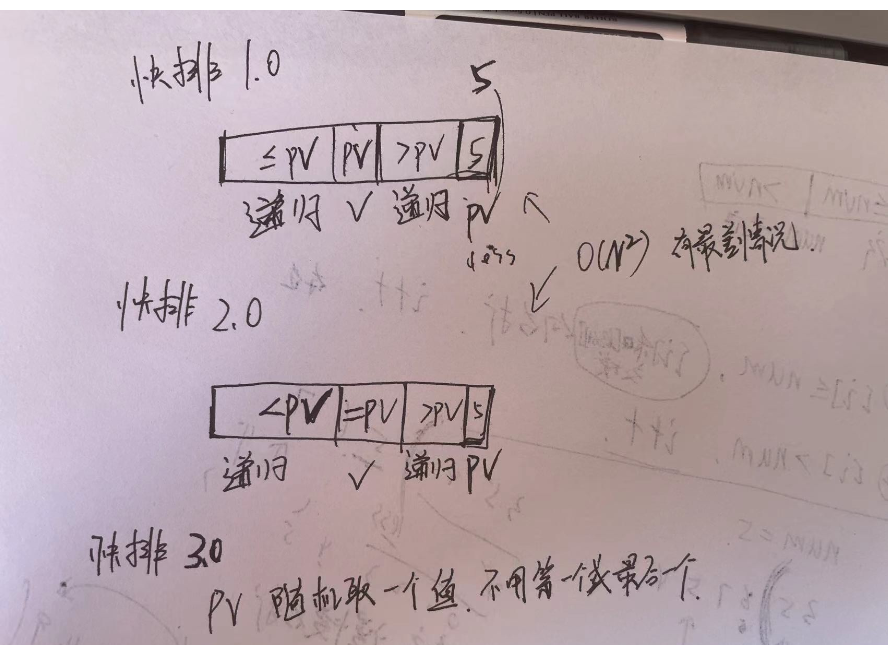
快排
- 快排1.0 2.0 3.0 的区别
![]()
快排1.0
func QuickSort_10(arr []int) {
partation_01(arr, 0, len(arr)-1)
}
func partation_01(arr []int, l int, r int) {
if l >= r {
return //递归结束条件
}
pv := arr[r]
less := l - 1
i := l
for ; i < r; i++ {
// 如果当前数小于 等于 num
if arr[i] <= pv {
swap(arr, less+1, i) //小于等于 区域右扩
less++
}
}
swap(arr, less+1, r) // 为啥这里需要替换呢。因为i < r ,最小区域less固定了,less +1 就是 pv的位置。
// 递归调用左右数组
partation_01(arr, l, less)
partation_01(arr, less+2, r)
}
快排2.0
func partation_02(arr []int, l int, r int) {
if l >= r {
return //递归结束条件
}
pv := arr[r]
less := l - 1
more := r + 1
i := l
for i < more {
// 如果当前数小于 等于 num
if arr[i] < pv {
swap(arr, less+1, i) //小于等于 区域右扩
less++
i++
} else if arr[i] == pv {
i++
} else {
swap(arr, i, more-1)
more--
}
}
if more <= r { //这里需要判断 more是否没扩。不然越界
swap(arr, more, r) //将 pv 也就是[r] 和more区域里的第一个值替换。
}
// swap(arr, more, r) //将 pv 也就是[r] 和more区域里的第一个值替换。
// 递归调用左右数组
partation_02(arr, l, less)
partation_02(arr, more, r)
}
快排3.0
func partation_03(arr []int, l int, r int) {
if l >= r {
return //递归结束条件
}
random_index := rand.Intn(r - l + 1) //随机选取一个索引
pv := arr[l+random_index]
// 将随机索引的数和最后一个数替换,下面的代码就和以前的一致了
swap(arr, l+random_index, r)
less := l - 1
more := r + 1
i := l
for i < more {
// 如果当前数小于 等于 num
if arr[i] < pv {
swap(arr, less+1, i) //小于等于 区域右扩
less++
i++
} else if arr[i] == pv {
i++
} else {
swap(arr, i, more-1)
more--
}
}
if more <= r {
swap(arr, more, r) //将 pv 也就是[r] 和more区域里的第一个值替换。
}
// 递归调用左右数组
partation_03(arr, l, less)
partation_03(arr, more, r)
}
好了ok.完事。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号