PCA principal component analysis
主成分分析是一个快速灵活的数据降维无监督方法，
可视化一个包含200个数据点的二维数据集
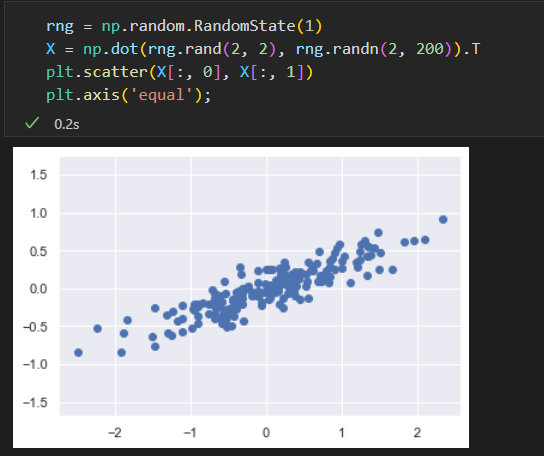
x 和 y有线性关系，无监督学习希望探索x值和y值之间的相关性
在主成分分析中。一种量化俩变量之间关系的方法 是在数据中找到一组主轴，并用这些主轴来描述 数据集。
利用PCA评估器
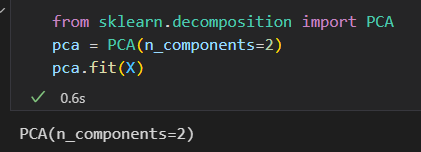
该拟合从数据中心学习到了一些指标，其中最重要的是 “成分” 和 “可解释差异”
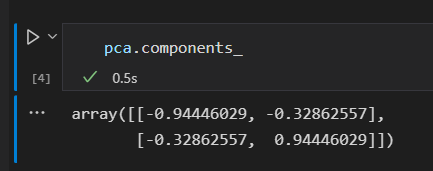
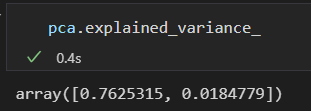
在数据图上将这些指标以向量形式画出来。
成分 定义向量的方向。
可解释差异 作为向量的平方长度。
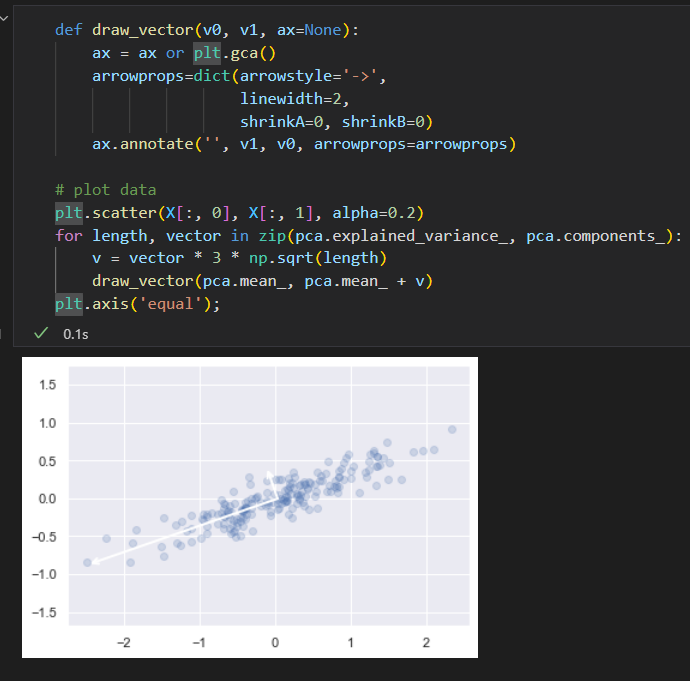
这些向量表示数据主轴，箭头长度表示输入数据中各个轴的 重要程度，衡量了数据投影到主轴上的方差的大小。
每个数据点在主轴上的投影就是数据 的主成分
这种从数据的坐标轴变换到主轴的编号 是一个 仿射变换，
仿射变换包含 平移 translation 旋转 rotation 均匀缩放 uniform scaling
用PCA降维
用PCA降为意味着去除一个 或 多个 最小主成分，从而得到一个更低维度且保留最大数据方差的数据投影。
PCA降维示例：
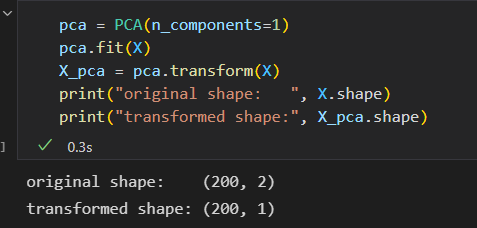
变换的数据投影到一个单一维度。
把降维的数据进行逆变换 ，来和原始数据对比
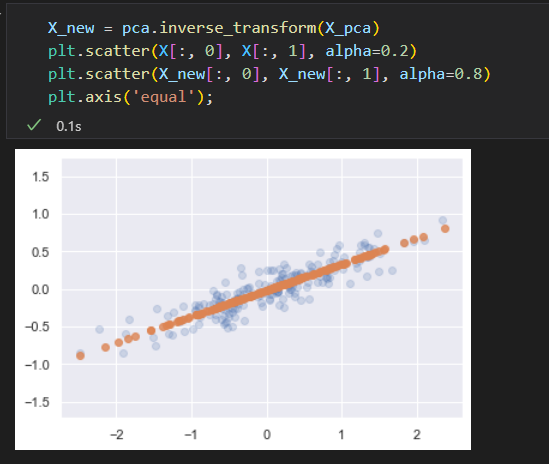
可以看出，沿着最不重要的主轴的信息都被去除了，仅留下了含有最高方差值得数据成分。
这种降维后的数据集在某种程度上足以体现数据中最主要的关系
用PCA作数据可视化：手写数字
降维的有用之处在俩个维度时不明显。 当数据维度很高是，价值就有所体现。
导入数据：
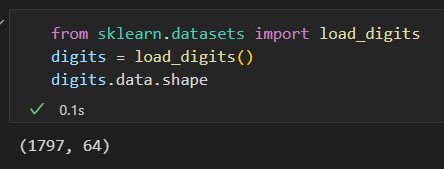
该数据包含 8* 8 像素的图像。是64维的。 将这些数据投影到一个可操作的维度。 二维
画出每个点的前俩个主成分，
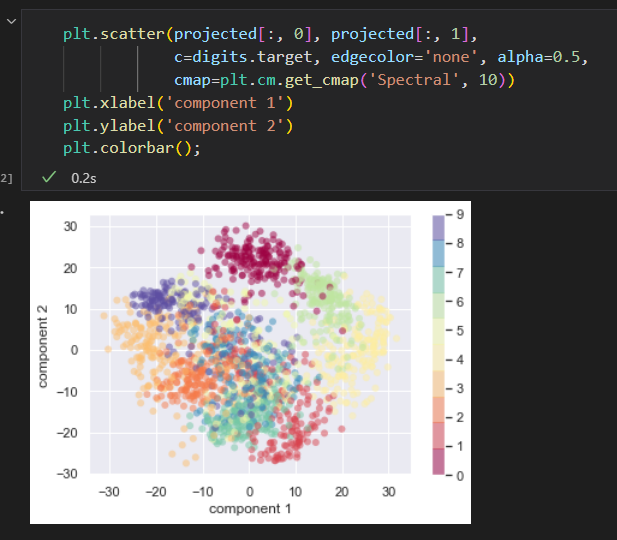
成分的含义：
消减的维度有什么含义？
每幅图像 由一组 64像素值 的 集合定义。将其称为 向量x
x=[x1,x2,x3⋯x64]
为了构建一幅图像，将向量的每个元素与对应描述的像素（单位列向量）相乘，然后将这些结果加和就是这幅图像
image(x)=x1⋅(pixel 1)+x2⋅(pixel 2)+x3⋅(pixel 3)⋯x64⋅(pixel 64)
我们可以将降维理解为删除绝大部分元素，保留少量元素的基向量，basis vector .
仅使用前8个像素，我们会得到数据的8维投影，但是它并不能反映整幅图像。
上面一行是单独的像素信息，下面一行是这些像素值的累加，累加值最终构成这幅图像。
但是逐像素表示方法并不是选择基向量的唯一方式，我们可以使用其他基函数，这些基函数包含预定义的每个像素的贡献。
PCA可以被认为 是选择最优基函数的过程，这样将这些基函数中前几个加起来就足以重构数据中 的大部分元素。
用低维形式表现数据的主成分，
用均值加上前8个PCA基函数重构数字的效果。
