support vector machine SVM
是非常强大、 灵活的有监督学习算法, 可以用于分类和回归。
贝叶斯分类器,对每个类进行了随机分布的假设,用生成的模型估计 新数据点 的标签。是属于 生成分类 方法。
判别分类:不再为每类数据建模,而是用一条分割线 或者 流形体 将各种类型分开。
原始数据:
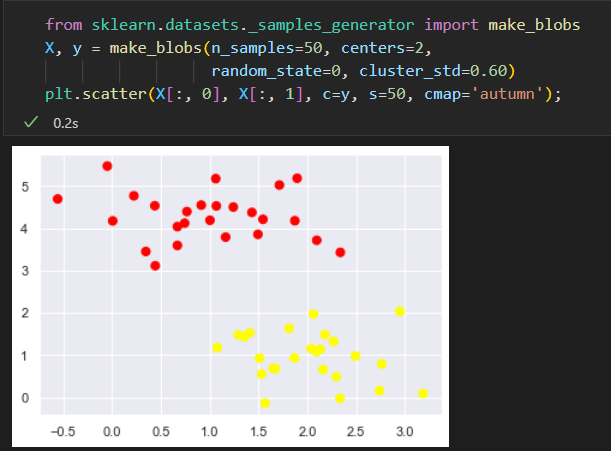
线性判别分类器 尝试 化一条 将数据 分成 俩部分的直线,这样就构成了一个分类模型。
可以发现不止一条直线可以将它们完美分割。
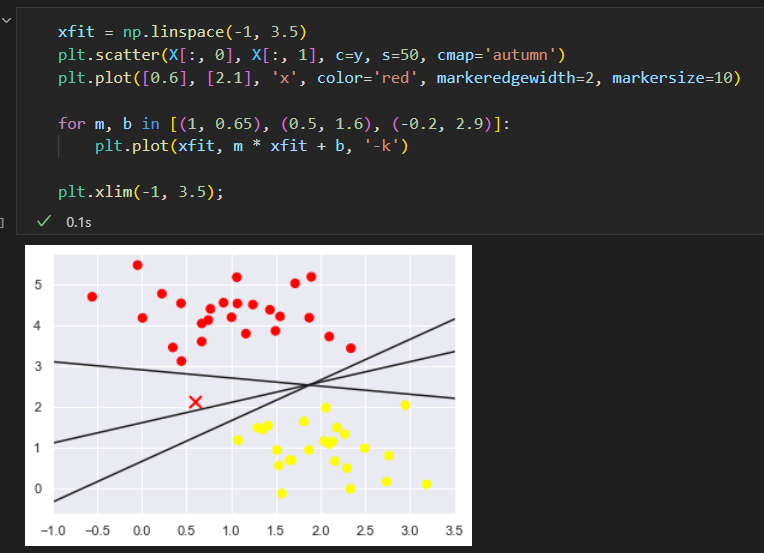
不同的分割线,会让新数据分配到不同的标签。
支持向量机:边界最大化
不是画一条细线来区分,而是画一条到最近点 边界 、有宽度 的线条。
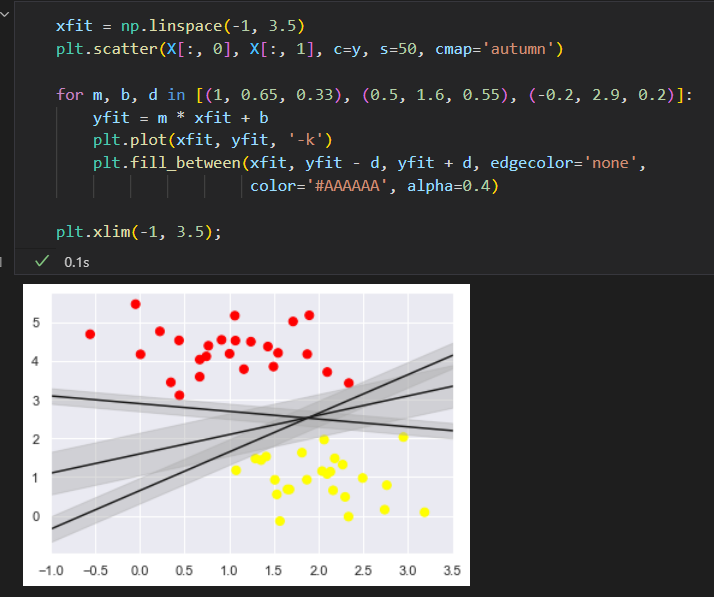
在支持向量机中,选择边界最大的那条线,是模型最优解。 边界最大化评估器。
拟合支持向量机
训练一个SVM模型,用一个线性核函数。并将参数C设置为一个很大的数。
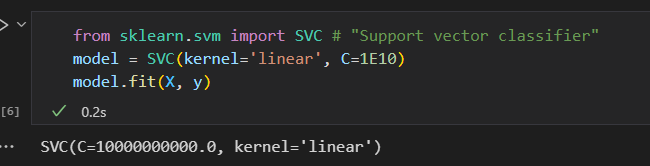
创建一个辅助函数画出SVM的决策边界。
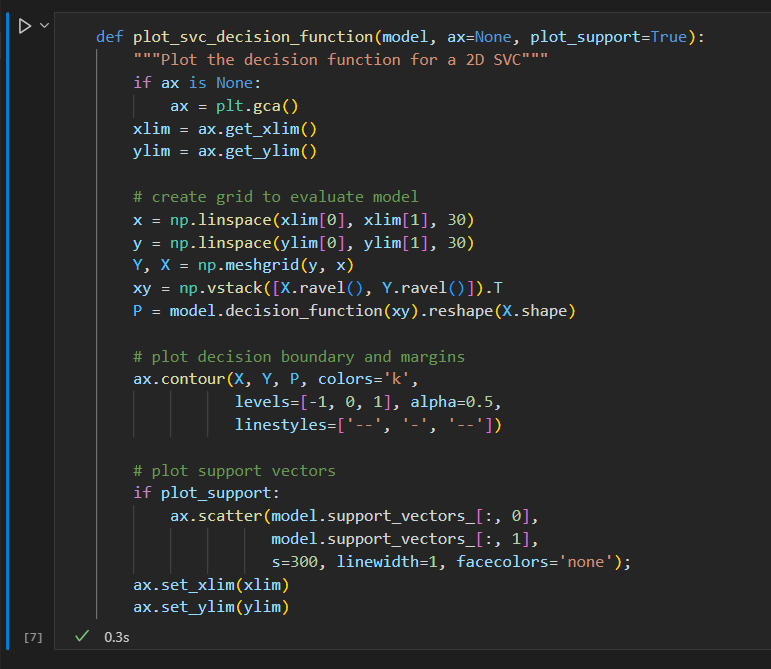
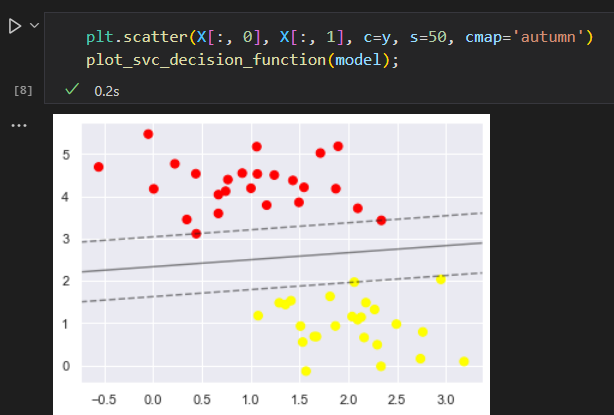
一些点正好在边界线上,这些点是拟合的关键支持点。被称为支持向量
支持向量的左边存放在分类器的support_vectors_ 属性中。
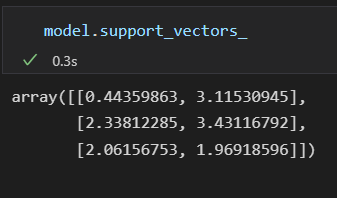
说明:任何在正确分类一侧远离边界线的点都不影响拟合结果。 因为这些点不会对拟合模型的损失函数产生任何影响,只要它们没跨越边界线,位置和数量就都无关紧要。
超越线性边界:核函数 SVM模型
将SVM模型 与 核函数 组合使用。功能会非常强大。
为了应用核函数,引入一些非线性可分数据。
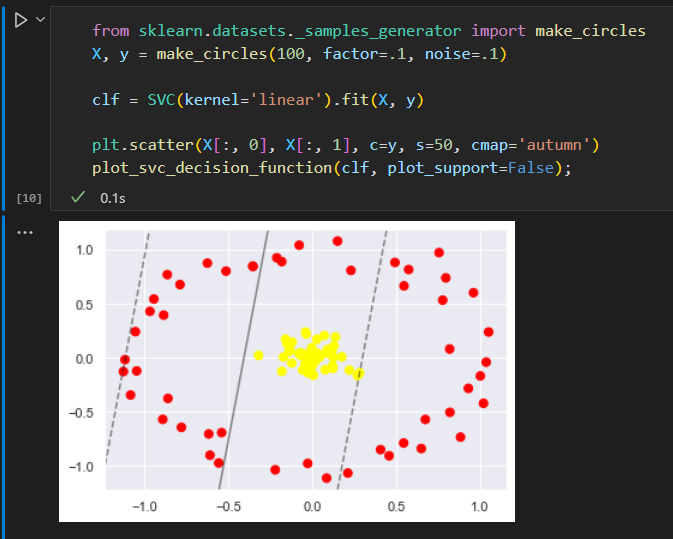
前面学到过,把数据投影到高维空间。从而使线性分割器派上用场。
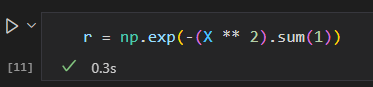
一个简单的投影方法就是计算一个以 数据圆圈 为中心的径向基函数:
用三维图来可视化新增的维度
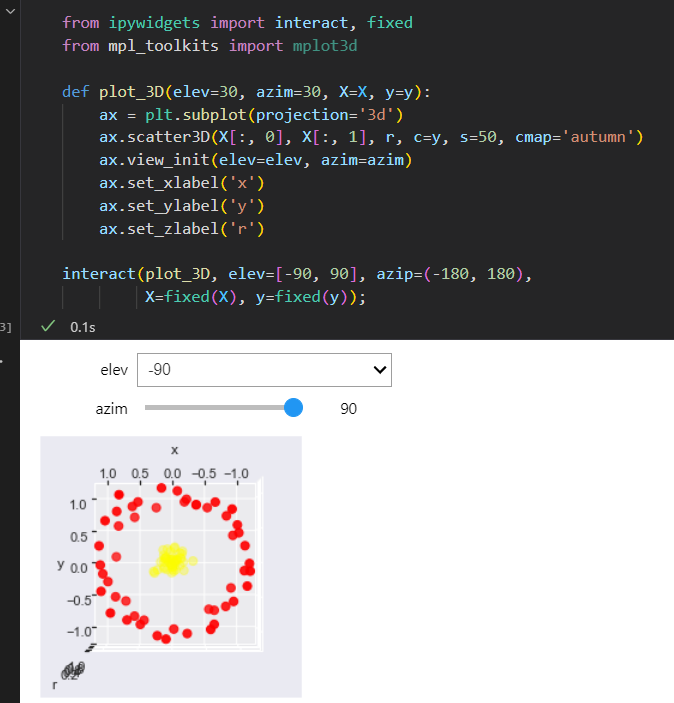
增加新的维度后,数据变成了线性可分状态,
通常选择基函数比较困难,我们需要让模型自动 指出 最合适的基函数。
一种 策略是计算基函数在数据集 上每个点的 变换结果,让SVM算法从所有结果中筛选出最优解。
这种基函数变换方式被称为 核变换
问题是:当N不断增大的时候,就会出现维度灾难。计算量巨大,
由于核函数技巧提供的小程序可以隐式计算 核变换数据的拟合。
在Scikit-Learn里面,我们可以应用核函数化的SVM模型,将线性核转变为 RBF (径向基函数)核。 设置kernel模型超参数即可。
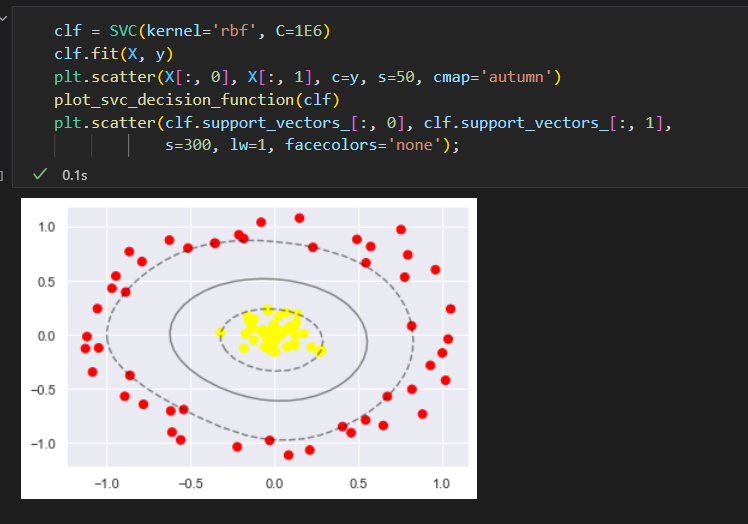
SVM优化:软化边界
如果数据有重叠,SVM实现了一些修正因子来“软化”边界,为了取得更好的拟合效果,允许一些点位于边界线之内。
边界线的硬度可以通过超参数进行控制,通常是C,
如果C很大,边界就会很硬,数据点便不能在边界内生存,
如果C比较小,边界就会较软,有一些数据点就可以穿越边界线。
案例:人脸识别
支持向量机总结
优点:
- 模型依赖的支持向量比较少,说明它们都是非常精致的模型,消耗内存少。
- 一旦模型训练完成,预测阶段速度非常快
- 由于模型只收边界线附近 的 点的影响,因此它们对于高维数据的学习效果非常好
- 与核函数方法的配合 极具通用性,能够适用不同类型的数据
缺点: - 随着样本量N的不断增加,最差的训练时间复杂度会达到O[N^3] .大样本学习的计算成本高
- 训练效果非常依赖于边界软化参数C的选择是否合理,这需要通过交叉检验自行搜索




