HDU 1541 Stars (线段树||树状数组)
Stars
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4897 Accepted Submission(s): 1934
Problem Description
Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.
![]()
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
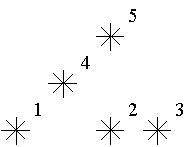
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.
You are to write a program that will count the amounts of the stars of each level on a given map.
Input
The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.
Output
The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.
Sample Input
5
1 1
5 1
7 1
3 3
5 5
Sample Output
1
2
1
1
0
Source
题目的意思是统计每个等级星星的个数,某一个星星的等级等于这个位于这个星星左下方的星星的个数
因为题目给出的数据时按照Y的升序排的,所以每次只用统计X坐标中1~X的星星的个数
有线段树和树状数组的做法,个人感觉树状数组会简单一些
树状数组:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<stdlib.h> 5 #include<algorithm> 6 using namespace std; 7 const int MAXN=32000+10; 8 const int N=15000+10; 9 int cnt[N],c[MAXN]; 10 int lowbit(int x) 11 { 12 return x&(-x); 13 } 14 int update(int i,int val) 15 { 16 while(i<=MAXN) 17 { 18 c[i]+=val; 19 i+=lowbit(i); 20 } 21 } 22 int sum(int i) 23 { 24 int ans=0; 25 while(i>0) 26 { 27 ans+=c[i]; 28 i-=lowbit(i); 29 } 30 return ans; 31 } 32 int main() 33 { 34 int n; 35 int x,y; 36 while(scanf("%d",&n)!=EOF) 37 { 38 memset(cnt,0,sizeof(cnt)); 39 memset(c,0,sizeof(c)); 40 for(int i=0;i<n;i++) 41 { 42 scanf("%d %d",&x,&y); 43 cnt[sum(x+1)]++; 44 update(x+1,1); 45 } 46 for(int i=0;i<n;i++) 47 printf("%d\n",cnt[i]); 48 } 49 return 0; 50 }
线段树:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<stdlib.h> 5 #include<algorithm> 6 using namespace std; 7 const int MAXN=15000+10;//点最大数 8 const int N=32000+10;//坐标最大 9 struct node 10 { 11 int l,r; 12 int num; 13 int mid() 14 { 15 return (l+r)/2; 16 } 17 }a[MAXN*6+10]; 18 int Count[MAXN+10]; 19 int n; 20 void btree(int step,int l,int r) 21 { 22 a[step].l=l; 23 a[step].r=r; 24 a[step].num=0; 25 if(l==r) 26 return ; 27 int mid=a[step].mid(); 28 btree(step*2,l,mid); 29 btree(step*2+1,mid+1,r); 30 } 31 void ptree(int step,int val) 32 { 33 if(a[step].l==a[step].r && a[step].l==val) 34 { 35 a[step].num++; 36 return ; 37 } 38 int mid=a[step].mid(); 39 if(val<=mid) 40 ptree(step*2,val); 41 else 42 ptree(step*2+1,val); 43 a[step].num=a[step*2].num+a[step*2+1].num; 44 } 45 int qtree(int step,int L,int R) 46 { 47 if(L<=a[step].l && a[step].r<=R) 48 return a[step].num; 49 int mid=a[step].mid(); 50 if(mid<L) 51 return qtree(step*2+1,L,R); 52 else if(R<=mid) 53 return qtree(step*2,L,R); 54 else 55 return qtree(step*2,L,R)+qtree(step*2+1,L,R); 56 } 57 int main() 58 { 59 while(scanf("%d",&n)!=EOF) 60 { 61 btree(1,0,N); 62 for(int i=0;i<n;i++) 63 Count[i]=0; 64 for(int i=0;i<n;i++) 65 { 66 int x,y,temp; 67 scanf("%d %d",&x,&y); 68 Count[qtree(1,0,x)]++; 69 ptree(1,x); 70 } 71 for(int i=0;i<n;i++) 72 printf("%d\n",Count[i]); 73 } 74 return 0; 75 }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号