TensorFlow非线性回归--基于神经网络算法

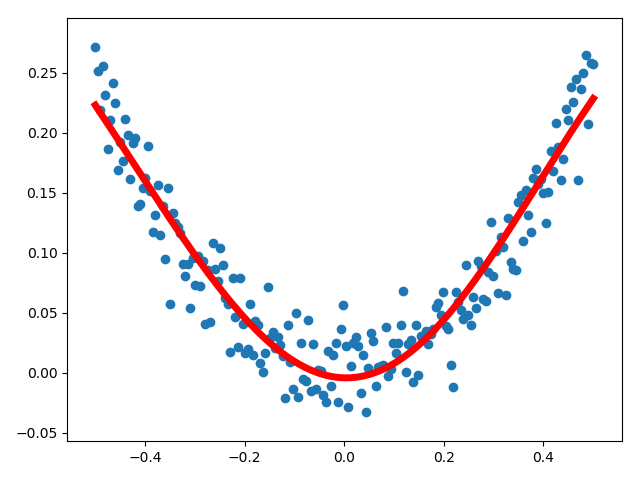
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

"""
1.
shape: 矩阵维度 3*2
===================
2.
[None,1]: N行 1列
===================
3.
numpy.random.normal(loc=0.0, scale=1.0, size=None)
正态分布
loc：float
    此概率分布的均值（对应着整个分布的中心centre）
scale：float
    此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
size：int or tuple of ints
    输出的shape，默认为None，只输出一个值

"""
xdata = np.linspace(-0.5, 0.5, 200)[:,np.newaxis]  # 后面增加维度
noise = np.random.normal(0, 0.02, xdata.shape)  # 加噪音，但要 保证和xdata的维度一致
ydata = np.square(xdata) + noise  # y=x^2+noise
# ydata=np.exp(xdata)+noise

# 定义两个placeholder
x = tf.placeholder(tf.float32, [None, 1])  # N行，1列
y = tf.placeholder(tf.float32, [None, 1])  # N行，1列，根据样本（x）定义
"""
输入层：x，输入就是一个个的点，那么就需要1个神经元就行
中间层：自定义
输出层：y，输出也是一个个的 点，配1个神经元
"""

# 定义神经网络中间层

weight = tf.Variable(tf.random_normal([1, 10]))  # 权值，连接输入层和中间层， 从正态分布中输出随机值,1（1个输入）行10（输入至中间层）列，权值放在线之上
biases = tf.Variable(tf.zeros([1, 10]))  # 偏置值，初始化为0，从一个输入，到10个中间层神经元
wx_plus_b_l1 = tf.matmul(x, weight) + biases  # 信号总和 weight*x+biases
l1 = tf.nn.tanh(wx_plus_b_l1)  # 激活函数，s形

# 定义输出层
"""
中间层的输出L1：输出层的输入
"""

weight1 = tf.Variable(tf.random_normal([10, 1]))  # 由中间层到y（输出），1-->10
biases1 = tf.Variable(tf.zeros([1, 1]))  # 偏置值，1-->1
wx_plus_b_l2 = tf.matmul(l1, weight1) + biases1  # 输出层信号总和
predict = tf.nn.tanh(wx_plus_b_l2)  # 预测的结果

# 二次代价函数
loss = tf.reduce_mean(tf.square(y - predict))  # 误差平均值

# 梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

#
with tf.Session() as ses:
    # 画变量
    ses.run(tf.global_variables_initializer())
    for _ in range(5001):
        ses.run(train_step, feed_dict={x: xdata, y: ydata})  # 使用梯度下降法训练, x：样本点

        # 得到预测值
    predict_value = ses.run(predict, feed_dict={x: xdata, y: ydata})
        # 画图
    plt.figure()
    plt.scatter(xdata, ydata)
    plt.plot(xdata, predict_value, 'r-', lw=5)  # 红色实线,线宽line width=5
    plt.show()