相位展开

The notions of Instantaneous Phase and Instantaneous Frequency are important concepts in Signal Processing that occur in the context of the representation and analysis of time-varying signals ^[1]. In signal processing, the instantaneous phase (or "local phase" or simply "phase") of a complex-valued function    is the real-valued function:

  (see arg function)

And for a real-valued signal    it is determined from the signal's analytic representation,  :

When is constrained to an interval such as    or 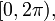   it is called the wrapped phase.  Otherwise it is called unwrapped, which is a continuous function of argument assuming 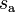is a continuous function of  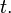  Unless otherwise indicated, the continuous form should be inferred.

 

from wiki