算法--字符串：最长回文子序列

转自：labuladong公众号

---

子序列问题是常见的算法问题，而且并不好解决。

　　首先，子序列问题本身就相对子串、子数组更困难一些，因为前者是不连续的序列，而后两者是连续的，就算穷举都不容易，更别说求解相关的算法问题了。

　　而且，子序列问题很可能涉及到两个字符串，比如让你求两个字符串的 最长公共子序列，如果没有一定的处理经验，真的不容易想出来。所以本文就来扒一扒子序列问题的套路，其实就有两种模板，相关问题只要往这两种思路上想，十拿九稳。

一般来说，这类问题都是让你求一个最长子序列，一旦涉及到子序列和最值，那几乎可以肯定，考察的是动态规划技巧，时间复杂度一般都是 O(n^2)。

一、两种思路

1、第一种思路模板是一个一维的 dp 数组：

int n = array.length;
int[] dp = new int[n];

for (int i = 1; i < n; i++) {
    for (int j = 0; j < i; j++) {
        dp[i] = 最值(dp[i], dp[j] + ...)
    }
}

　　举个我们写过的例子 最长递增子序列，在这个思路中 dp 数组的定义是：

　　在子数组array[0..i]中，以array[i]结尾的目标子序列（最长递增子序列）的长度是dp[i]。

　　为啥最长递增子序列需要这种思路呢？前文说得很清楚了，因为这样符合归纳法，可以找到状态转移的关系，这里就不具体展开了。

2、第二种思路模板是一个二维的 dp 数组：

int n = arr.length;
int[][] dp = new dp[n][n];

for (int i = 0; i < n; i++) {
    for (int j = 1; j < n; j++) {
        if (arr[i] == arr[j]) 
            dp[i][j] = dp[i][j] + ...
        else
            dp[i][j] = 最值(...)
    }
}

　　这种思路运用相对更多一些，尤其是涉及两个字符串/数组的子序列。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。

　　2.1 涉及两个字符串/数组时（比如最长公共子序列），dp 数组的含义如下：

　　　　在子数组arr1[0..i]和子数组arr2[0..j]中，我们要求的子序列（最长公共子序列）长度为dp[i][j]。

　　2.2 只涉及一个字符串/数组时（比如本文要讲的最长回文子序列），dp 数组的含义如下：

　　　　在子数组array[i..j]中，我们要求的子序列（最长回文子序列）的长度为dp[i][j]。

　　第一种情况可以参考这两篇旧文：详解编辑距离 和 最长公共子序列。

---

二、最长回文子序列

之前解决了 最长回文子串 的问题，这次提升难度，求最长回文子序列的长度：

　　

我们说这个问题对 dp 数组的定义是：在子串s[i..j]中，最长回文子序列的长度为dp[i][j]。一定要记住这个定义才能理解算法。

为啥这个问题要这样定义二维的 dp 数组呢？我们前文多次提到，找状态转移需要归纳思维，说白了就是如何从已知的结果推出未知的部分，这样定义容易归纳，容易发现状态转移关系。

具体来说，如果我们想求dp[i][j]，假设你知道了子问题dp[i+1][j-1]的结果（s[i+1..j-1]中最长回文子序列的长度），你是否能想办法算出dp[i][j]的值（s[i..j]中，最长回文子序列的长度）呢？

　　

可以！这取决于s[i]和s[j]的字符：

如果它俩相等，那么它俩加上s[i+1..j-1]中的最长回文子序列就是s[i..j]的最长回文子序列：

　　　　

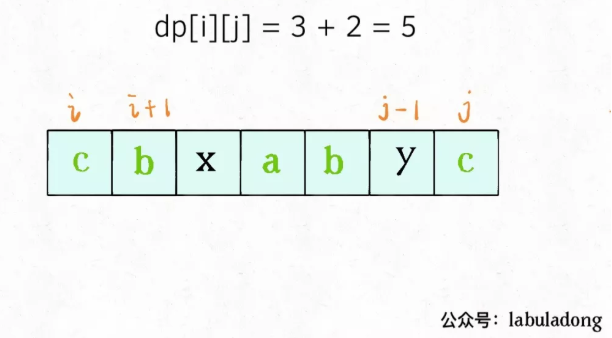
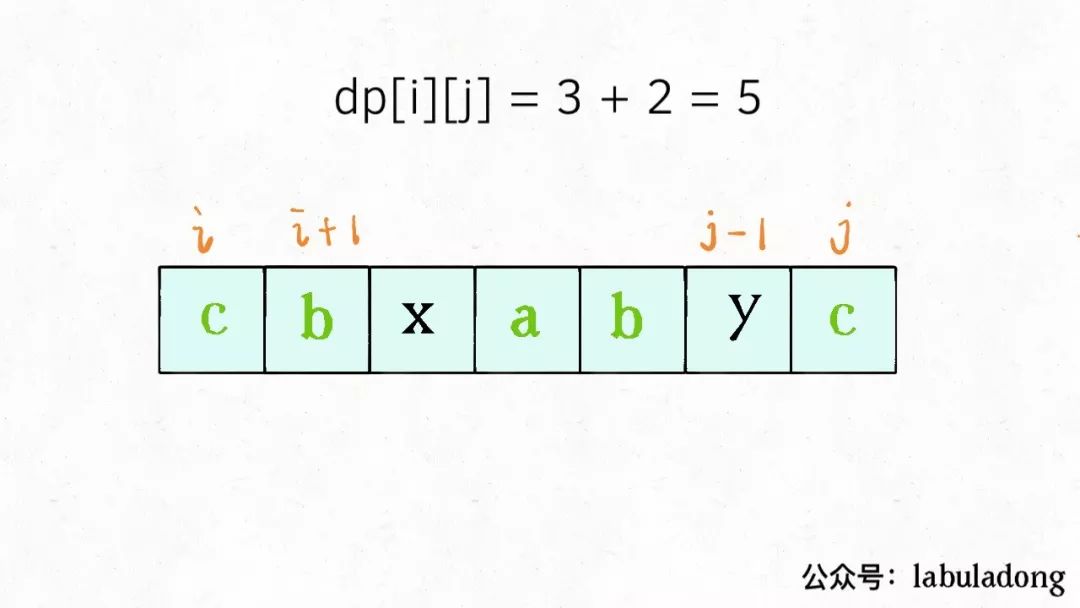
如果它俩不相等，说明它俩不可能同时出现在s[i..j]的最长回文子序列中，那么把它俩分别加入s[i+1..j-1]中，看看哪个子串产生的回文子序列更长即可：

　　

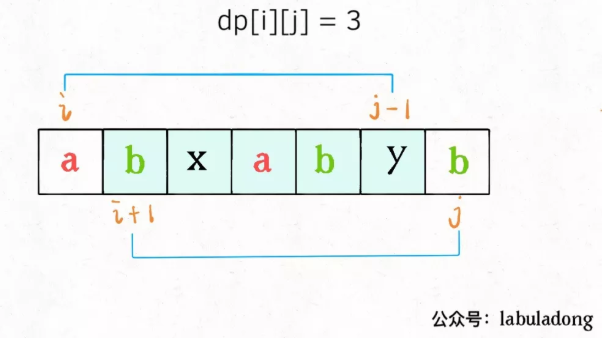
以上两种情况写成代码就是这样：

if (s[i] == s[j])
    // 它俩一定在最长回文子序列中
    dp[i][j] = dp[i + 1][j - 1] + 2;
else
    // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

至此，状态转移方程就写出来了，根据 dp 数组的定义，我们要求的就是dp[0][n - 1]，也就是整个s的最长回文子序列的长度。

三、代码实现

首先明确一下 base case，如果只有一个字符，显然最长回文子序列长度是 1，也就是dp[i][j] = 1,(i == j)。

因为i肯定小于等于j，所以对于那些i > j的位置，根本不存在什么子序列，应该初始化为 0。

另外，看看刚才写的状态转移方程，想求dp[i][j]需要知道dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1]这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：

　　

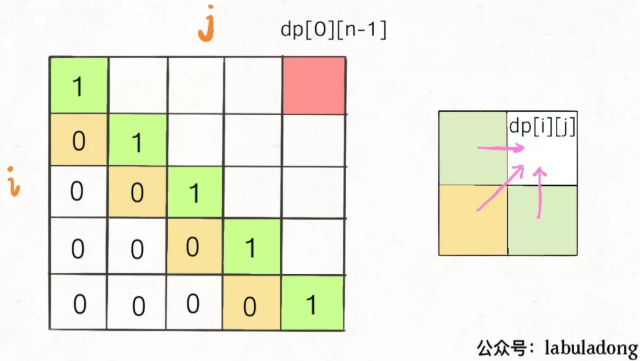
为了保证每次计算dp[i][j]，左、下、左下三个方向的位置已经被计算出来，只能斜着遍历或者反着遍历：

　　

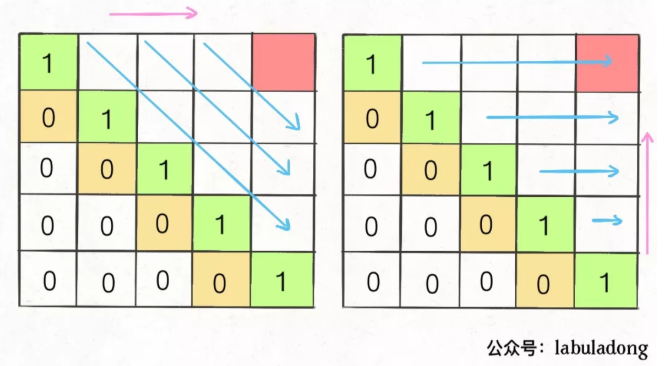
选择反着遍历，代码如下：

int longestPalindromeSubseq(string s) {
    int n = s.size();
    // dp 数组全部初始化为 0
    vector<vector<int>> dp(n, vector<int>(n, 0));
    // base case
    for (int i = 0; i < n; i++)
        dp[i][i] = 1;
    // 反着遍历保证正确的状态转移
    for (int i = n - 1; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // 状态转移方程
            if (s[i] == s[j])
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 整个 s 的最长回文子串长度
    return dp[0][n - 1];
}

主要还是正确定义 dp 数组的含义，遇到子序列问题，首先想到两种动态规划思路，然后根据实际问题看看哪种思路容易找到状态转移关系。

另外，找到状态转移和 base case 之后，一定要观察 DP table，看看怎么遍历才能保证通过已计算出来的结果解决新的问题