树状数组

前缀和之树状数组

树状数组（Fenwick Tree）是一种用于高效处理区间查询与修改的重要工具。它可以在 (O(log n)) 的时间复杂度内完成单点更新和前缀区间求和的操作。

一、树状数组的基本思想

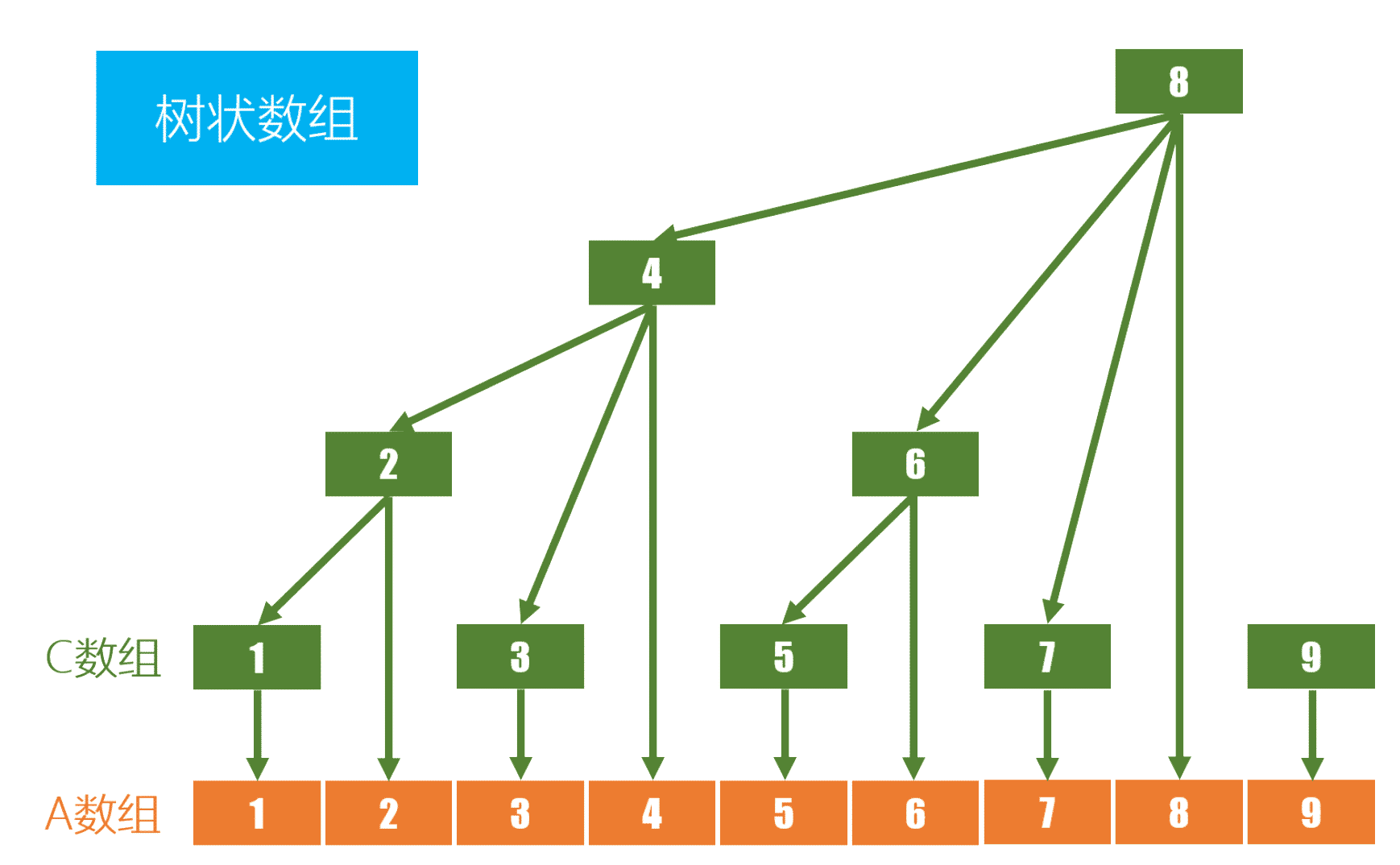
树状数组通过一个辅助数组 (c[i]) 实现，将原数组的信息以一种特殊的方式存储，使得查询和更新都能快速完成。其核心思想是利用数组的二进制表示，按区间段存储部分和。

例如，假设数组下标从 (1) 开始：

• (c[i]) 保存的是从 (i) 减去 (lowbit(i)) 再加 (1) 到 (i) 的区间和。这里的 (lowbit(i)) 表示 (i) 的二进制表示中最低位的 (1) 所对应的值，其计算方式是 (lowbit(x)=x) 与 (-x) 的按位与运算结果（即 (lowbit(x)=x & (-x))）。
  

二、树状数组的结构特点

通过树状数组，我们可以快速实现以下两个操作：

（一）单点更新

更新数组中的某个值，同时维护相关区间和。

（二）区间查询

计算从起点到某点的前缀和。

1. 示例：计算前缀和

以数组 (a[1..n]) 为例，假设使用树状数组存储信息，我们可以用如下伪代码完成前缀和计算：

// 查询从索引1到指定index的前缀和
    public int query(int index) {
        int res = 0;
        while (index > 0) {
            res += tree[index];
            index -= index & -index;
        }
        return res;
    }

2. 示例：单点更新

当我们想更新 (a[k]) 的值（例如加上 (y)），树状数组中的相关节点也需要同步更新。具体实现如下：

// 对指定索引index处的元素进行单点更新，增加val的值
    public void add(int index, int val) {
        while (index <= n) {
            tree[index] += val;
            index += index & -index;
        }
    }

三、树状数组的实际应用

树状数组具有广泛的实际应用，特别是在需要频繁查询和更新的场景中：

（一）区间求和问题

计算任意子区间的和。

（二）动态排序统计

例如，求解逆序对数。

（三）二维平面问题

如处理棋盘上的子矩阵求和。

代码实现

以下是树状数组的基本实现代码：

public class BinaryIndexedTree {
    // 表示树状数组所处理的序列长度
    private int n;
    // 树状数组本身
    private int[] tree;

    // 构造函数，用于初始化树状数组，这里假设传入的数组长度就是要处理的长度n
    public BinaryIndexedTree(int[] arr) {
        n = arr.length;
        tree = new int[n + 1];
        // 初始化树状数组，可根据具体需求调整初始化逻辑
        for (int i = 0; i < n; i++) {
            add(i + 1, arr[i]);
        }
    }

    // 查询从索引1到指定index的前缀和
    public int query(int index) {
        int res = 0;
        while (index > 0) {
            res += tree[index];
            index -= index & -index;
        }
        return res;
    }

    // 对指定索引index处的元素进行单点更新，增加val的值
    public void add(int index, int val) {
        while (index <= n) {
            tree[index] += val;
            index += index & -index;
        }
    }

    // 示例用法展示
    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9};
        BinaryIndexedTree bit = new BinaryIndexedTree(arr);

        // 查询索引为3的前缀和
        int prefixSum = bit.query(3);
        System.out.println("索引为3的前缀和: " + prefixSum);

        // 对索引为2的元素进行单点更新，增加2
        bit.add(2, 2);

        // 再次查询索引为3的前缀和
        prefixSum = bit.query(2);
        System.out.println("更新后索引为2的前缀和: " + prefixSum);
    }
}