万能欧几里得算法学习笔记

万能欧几里得算法

万能欧几里得算法用于解决一类与\(\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor\)有关的和式求解问题，例如类欧几里得算法中提到的和式就属于此类问题。但万能欧几里得算法从几何意义出发能处理更广泛的和式类型。例如\(\sum_{x=0}^{l}A^xB^{\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor}\quad A,B\subseteq \mathbb{R}^{n\times n}\)。

我们在平面直角坐标系中作出一条直线\(y=\frac{p\cdot x+r}{q}\)。以\(y=\frac{5x+3}{4}\)为例

我们注意到这条直线与平行于坐标轴的直线有若干个交点。与横线的交点（紫色），与竖线的交点（红色），如果同时与横线和竖线相交，我们约定先与横线相交再与竖线相交，这么做的原因我们等会会看到。

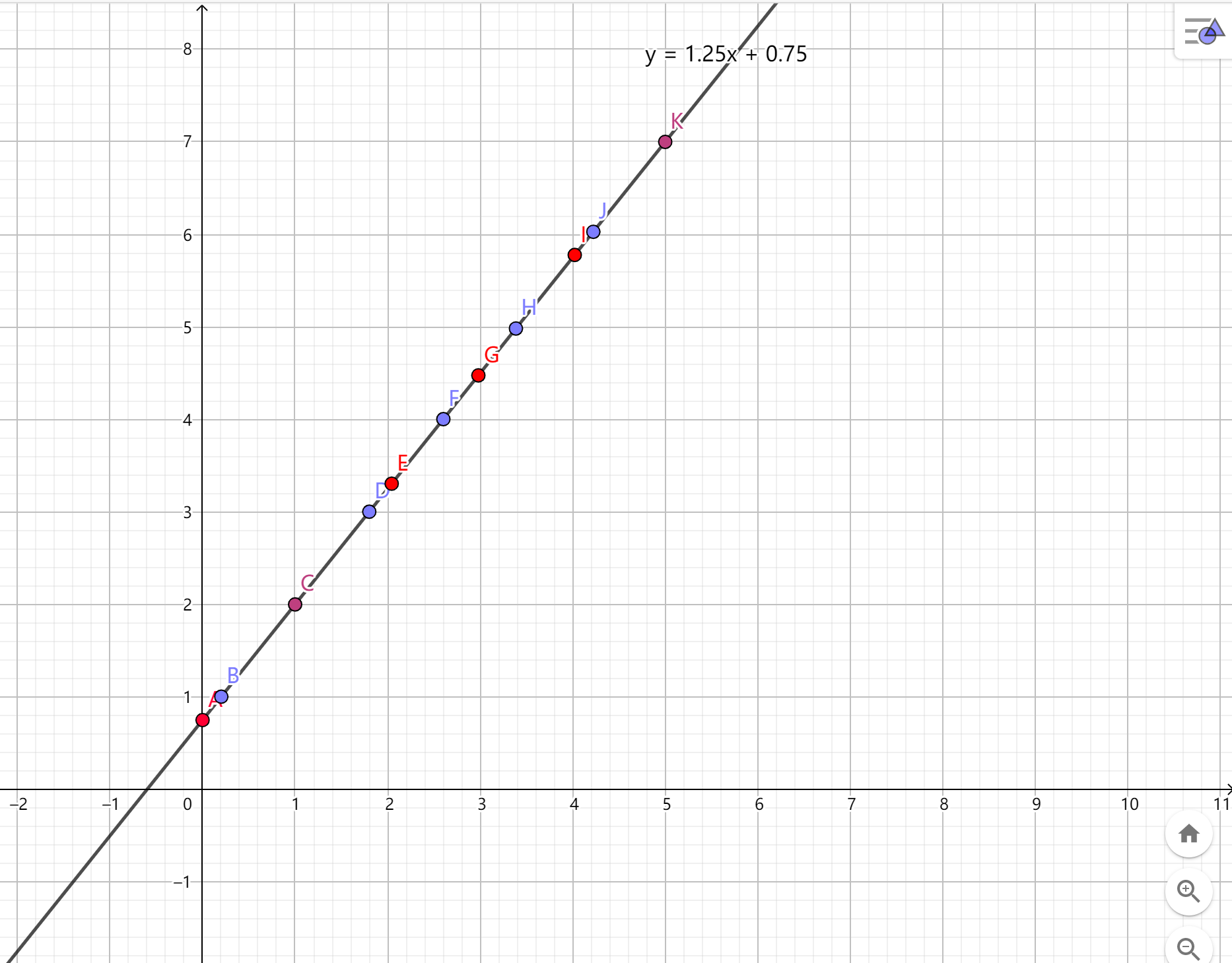
我们要求解的和式就可以看做，从初始状态开始，遇到横线做一种操作，遇到竖线做另一种操作最终得到答案。因为遇到横线意味着\(\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor\)会增加\(1\)，遇到竖线意味着\(x\)会增加\(1\)。

以开头提到的\(\sum_{x=0}^{l}A^xB^{\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor}\quad A,B\subseteq \mathbb{R}^{n\times n}\)为例，我们设定一个三元组\(\left( C,D,ans \right)\)来记录答案。

初始时\(C=D=I_n\quad ans=B^{\left\lfloor \frac{r}{q} \right\rfloor}\)，我们只需要关注\(\left( 0,l \right]\)范围内的交点，然后每经过一根横线，我们需要将\(D\text{右乘}B\)，\(C\text{和}ans\text{不变}\)。每经过一条竖线，我们需要将\(C\text{左乘}A，D保持不变，ans+A\cdot C\cdot D \rightarrow ans_{new}\)

对三元组形式化的理解是，\(C\)表示当前操作序列\(A^x\)的值，\(D\)表示当前操作序列\(B^{\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor}\)的值，\(ans\)表示当前操作序列对答案的贡献。这里我们可以明白一开始约定碰到与横线竖线同时相交的点要视作先碰横线再碰竖线，因为在碰到竖线的时候意味着\(x\)增加了\(1\)，需要更新答案了，先要把\(\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor\)更新到最新。

我们继续把上述操作用标准化的语言描述，定义三元组的乘法，\(\left( a,b,c \right) \ast (d,e,f)=(a\cdot d,b\cdot e,c+a\cdot f\cdot b)\quad a,b,c,d,e,f\subseteq \mathbb{R}^{n\times n}\text{，}a\text{,}d\text{是矩阵A的幂，}b\text{,}e\text{是矩阵}B\text{的幂}\)，碰上横线进行的操作是乘三元组\(\left( I_n,B,O_n \right)\)，碰上竖线进行的操作是乘三元组\(\left( A,I_n,A \right)\)。容易证明这个三元组的乘法具有结合律，事实上这也是万能欧几里得算法能解决问题的必要条件。

有了上面的储备，接下来就来看看怎么样加速求解的过程。方便起见，我们用\(s_0\)表示碰到横线需要执行的操作，\(s_1\)表示碰到竖线需要执行的操作。用\(solve(p,q,r,l,s_0,s_1)\)描述问题的求解过程。

• case0：对于\(r\)的处理。
  由于我们只关心交点到来的顺序以及交点的种类，因此将函数上下平移整数个单位是不影响答案的。我们把\(r\)修改为\(r\%q\)，后面我们都默认\(r<q\)。

• case1：\(p\ge q\)
  在这种情况下，我们可以发现：

  \[\left\lfloor \frac{p\cdot (x +1)+r}{q} \right\rfloor-\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor=\left\lfloor \frac{p\cdot x +(p\%q)+r}{q} \right\rfloor-\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor+\left\lfloor \frac{p}{q} \right\rfloor \ge \left\lfloor \frac{p}{q} \right\rfloor \]

  这说明在遇到一根竖线之前我们至少会遇到\(\left\lfloor \frac{p}{q} \right\rfloor\)条横线。这样就可以把这\(\left\lfloor \frac{p}{q} \right\rfloor\)个\(s_0\)操作和一个\(s_1\)操作合并成一个新的\(s_1\)操作。这样每条竖线之前会有\(\left\lfloor \frac{p}{q} \right\rfloor\cdot x\)条横线被合并

  \[\left\lfloor \frac{p\cdot x+r}{q} \right\rfloor-\left\lfloor \frac{p}{q} \right\rfloor\cdot x=\left\lfloor \frac{(p\%q)\cdot x+r}{q} \right\rfloor \]

  因此\(solve(p,q,r,l,s_0,s_1)=solve(p\%q,q,r,l,s_0,s_0^{\left\lfloor \frac{p}{q} \right\rfloor}s_1)\)

• case2：\(p<q\)
  我们可以想到把坐标轴翻转，把\(y=\frac{p\cdot x+r}{q}\)变为\(y=\frac{q\cdot x-r}{p}\)同时交换\(s_0,s_1\)这样就可以回归到case1中去了。但翻转过后我们发现三个小问题，第一个是对于同时和横线竖线相交的点，翻转之后变成了先做\(s_1\)再做\(s_0\)这与我们的期望不符，第二个是直线在\(y\)轴上的截距变成了负的；第三个是原先我们是以竖线结尾的，现在变成以横线结尾。这些问题导致处理起来会有麻烦。（下面的推到过程并不适用于\(p=1\)的情况，但我们之后会看到用下面推到过程得出的算法对于\(p=1\)确是正确的）
  我们先来解决第一个问题，

  \[\forall y \subseteq \mathbb{N}^*\text{且}q\cdot y-r\neq 0 \pmod p \\ \frac{q\cdot y-r}{p}-\left\lfloor \frac{q\cdot y-r}{p} \right\rfloor=\frac{q\cdot y-r-\left\lfloor \frac{q\cdot y-r}{p} \right\rfloor\cdot p}{p}=\frac{(q\cdot y-r)\% p}{p} \ge \frac{1}{p} \]

  因此我们可以将原函数向左平移\(\frac{1}{p}\)个单位再反转，这并不影响答案，同时又解决了同时和横线竖线相交的点。直线变成\(y=\frac{qx-r-1}{p}\)
  再来看剩下的两个问题。事实上，第二个问题对应翻转前\(y<1\)的情况，第三个问题对应翻转前\(y\ge \left\lfloor \frac{p\cdot l+r}{q} \right\rfloor\)的情况。我们可以掐头去尾把这两部分单独拿出来考虑。

  \[y=\frac{p\cdot x+r}{q}<1 \Leftrightarrow 0<x\leq \left\lfloor \frac{q-r-1}{p} \right\rfloor \\ y=\frac{p\cdot x+r}{q}\geq\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor\Leftrightarrow \left\lfloor \frac{\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor\cdot q-r-1}{p} \right\rfloor+1 \leq x \leq l \]

  这样我们只需要专注于\(\left( 1,\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor \right]\)内的交点即可。为了与最初的问题适配，我们把直线向左平移一个单位，并计算\(\left( 0,\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor-1 \right]\)内的交点。直线变成\(y=\frac{q\cdot x+q-r-1}{p}\)
  因此\(solve\left( p,q,r,l,s_0,s_1\right)=s_1^{\left\lfloor \frac{q-r-1}{p} \right\rfloor}\cdot s_0\cdot solve\left(q,p,q-r-1,\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor-1\right)\cdot s_1^{l-\left\lfloor \frac{\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor\cdot q-r-1}{p} \right\rfloor}\)

• case3：\(p=1\)
  我们再来看\(p=1\)的情况，\(p=1\)时，当\(y\)取到整数时，\(x\)也必然是整数，操作过程是规律性的\(q\)条竖线\(1\)条横线，\(q\)条竖线\(1\)条横线，\(\cdots\) 在case2的算法中我们掐头时，少算了经过\(y=1\)这个整点的一条竖线，然而在经过其他整点时由于横线竖线顺序是反的，刚好把这个误差补了回来，在去尾时，多算了经过\(y=\left\lfloor \frac{p\cdot l+r}{q} \right\rfloor\)时的一条竖线，刚好又把最后的误差给补足了。所以虽然case2的推导过程对\(p=1\)不适用，但导出的算法恰好适合\(p=1\)。真是太奇妙了。

现在我们完成了整个万能欧几里得算法，他和传统欧几里得算法的过程类似，时间复杂度是合并两个操作的时间复杂度乘上\(O(\log_2p)\)

code：万能欧几里得

#include <cstdio>
#include <cstring>
#include <iostream>
#define int long long

using namespace std;

const int mo = 998244353;

struct mat {
    int a[25][25];
    int n;
    void init(int n) {
        memset(a, 0, sizeof(a));
        this->n = n;
    }
    void read() {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                scanf("%lld", &a[i][j]);
            }
        }
    }
    void setI(int n) {
        this->n = n;
        memset(a, 0, sizeof(a));
        for (int i = 1; i <= n; i++) {
            a[i][i] = 1;
        }
    }
    mat operator+(const mat& o) const {
        mat ans;
        ans.init(n);
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                ans.a[i][j] += o.a[i][j];
                ans.a[i][j] += a[i][j];
                ans.a[i][j] %= mo;
            }
        }
        return ans;
    }
    mat operator*(const mat& o) const {
        mat ans;
        ans.init(n);
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                for (int k = 1; k <= n; k++) {
                    ans.a[i][j] += 1ll * a[i][k] * o.a[k][j] % mo;
                    ans.a[i][j] %= mo;
                }
            }
        }
        return ans;
    }
    void print() {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j < n; j++) {
                printf("%lld ", a[i][j]);
            }
            printf("%lld\n", a[i][n]);
        }
    }
} A, B;

struct pp {
    mat a;
    mat b;
    mat ans;
    int n;
    pp(int n) {
        a.setI(n);
        b.setI(n);
        ans.init(n);
        this->n = n;
    }
    pp(mat o, mat p, mat q, int n) {
        a = o;
        b = p;
        ans = q;
        this->n = n;
    }
    pp setA() {
        a.init(n);
        b.setI(n);
        a = ans = A;
        return *this;
    }
    pp setB() {
        a.setI(n);
        b.init(n);
        ans.init(n);
        b = B;
        return *this;
    }
    pp fix() {
        for (int i = 1; i <= n; i++) {
            ans.a[i][i]++;
            ans.a[i][i] %= mo;
        }
        return *this;
    }
    pp operator*(const pp& o) const {
        return pp(a * o.a, b * o.b, ans + a * o.ans * b, n);
    }
    pp pow(int p) {
        pp yu = pp(n);
        pp o = *this;
        while (p) {
            if (p & 1) yu = yu * o;
            o = o * o;
            p >>= 1;
        }
        return yu;
    }
};

int p, q, r, l, n;

pp slove(int p, int q, int r, int l, pp s0, pp s1) {
    r = r % q;
    if (p >= q) return slove(p % q, q, r, l, s0, s0.pow(p / q) * s1);
    int m = ((__int128)p * l + r) / q;
    if (m == 0) return s1.pow(l);
    return (s1.pow((q - r - 1) / p) * s0 *
            slove(q, p, q - r - 1, m - 1, s1, s0) *
            s1.pow(l - ((__int128)m * q - r - 1) / p));
}

signed main() {
    scanf("%lld%lld%lld%lld%lld", &p, &q, &r, &l, &n);
    A.init(n);
    A.read();
    B.init(n);
    B.read();
    pp s0 = pp(n).setB();
    pp s1 = pp(n).setA();
    pp ans = pp(n);
    ans.ans = s0.pow((p+r)/q).b;
    ans = ans * s0.pow((p + r) / q) * slove(p, q, p + r, l - 1, s0, s1);
    (A * ans.ans).print();
    return 0;
}