哈夫曼编码
哈夫曼编码是 1952 年由 David A. Huffman 提出的一种无损数据压缩的编码算法。哈夫曼编码先统计出每种字母在字符串里出现的频率,根据频率建立一棵路径带权的二叉树,也就是哈夫曼树,树上每个结点 存储字母出现的频率,根结点到结点的路径即是字母的编码,频率高的字母使用较短的编码,频率低的字母使用较长的编码,使得编码后的字符串占用空间最小。
首先统计每个字母在字符串里出现的频率,我们把每个字母看成一个结点,结点的权值即是字母出现的频率,我们把每个结点看成一棵只有根结点的二叉树,一开始把所有二叉树都放在一个集合里。接下来开始如下编码:
步骤一:从集合里取出两个根结点权值最小的树 a 和 b,构造出一棵新的二叉树 c,二叉树 c 的根结点的权值为 a 和 b 的根结点权值和,二叉树 c 的左右子树分别是 a 和 b。
步骤二:将二叉树 a 和 b 从集合里删除,把二叉树 c 加入集合里。
重复以上两个步骤,直到集合里只剩下一棵二叉树,最后剩下的就是哈夫曼树了。
我们规定每个有孩子结点的结点,到左孩子结点的路径为 0,到右孩子结点的路径为 1。每个字母的编码就是根结点到字母对应结点的路径。
例如有这一个字符串“good good study day day up”,现在我们要对字符串进行哈夫曼编码,该字符串一共有 26 个字符,10 种字符,我们首先统计出每个字符的频率,然后按从大到小顺序排列如下(第二列的字符是空格):

我们把每个字符看成一个结点,权值是字符的频率,每个字符开始都是一棵只有根结点的二叉树,如下图。

1.从集合里取出根结点权值最小的两棵树 I 和 J 组成新的二叉树 IJ,根结点权值为 1 + 1 = 2,将二叉树 IJ 加入集合,把 I 和 J 从集合里删除,如下图。
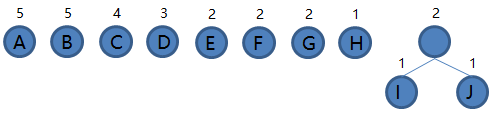
2.从集合里取出根结点权值最小的两棵树 H 和 G 组成新的二叉树 HG,根结点权值为 1 + 2 = 3,将二叉树 HG 加入集合,把 H 和 G 从集合里删除,如下图。
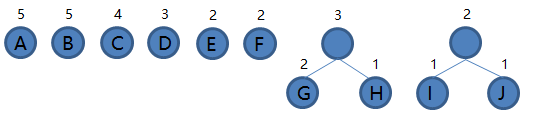
3.从集合里取出根结点权值最小的两棵树 E 和 F 组成新的二叉树 EF,根结点权值为 2 + 2 = 4,将二叉树 EF 加入集合,把 E 和 F 从集合里删除,如下图。
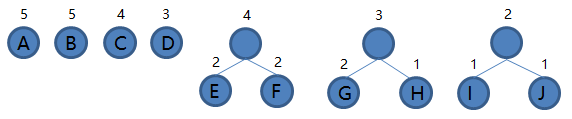
4.从集合里取出根结点权值最小的两棵树 IJ 和 D 组成新的二叉树 IJD,根结点权值为 2 + 3 = 5,将二叉树 IJD 加入集合,把 IJ 和 D 从集合里删除,如下图。
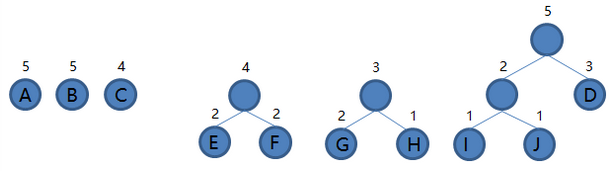
5.从集合里取出根结点权值最小的两棵树 GH 和 C 组成新的二叉树 GHC,根结点权值为 3 + 4 = 7,将二叉树 GHC 加入集合,把 GH 和 C 从集合里删除,如下图。
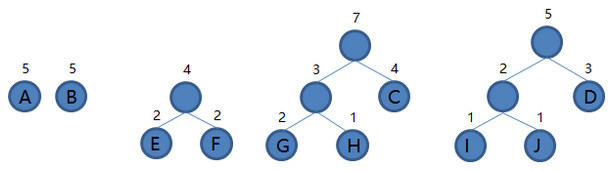
6.从集合里取出根结点权值最小的两棵树 EF 和 B 组成新的二叉树 EFB,根结点权值为 4 + 5 = 9,将二叉树 EFB 加入集合,把 EF 和 B 从集合里删除,如下图。
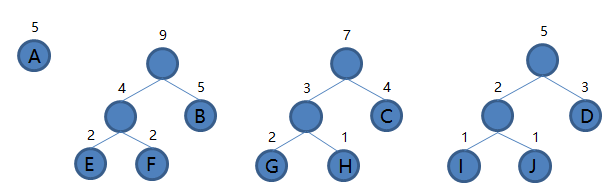
7.从集合里取出根结点权值最小的两棵树 IJD 和 A 组成新的二叉树 IJDA,根结点权值为 5 + 5 = 10,将二叉树 IJDA 加入集合,把 IJD 和 A 从集合里删除,如下图。
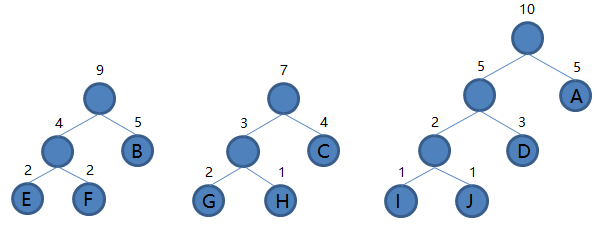
8.从集合里取出根结点权值最小的两棵树 EFB 和 GHC 组成新的二叉树 EFBGHC,根结点权值为 9 + 7 = 16,将二叉树 EFBGHC 加入集合,把 EFB 和 GHC 从集合里删除,如下图。
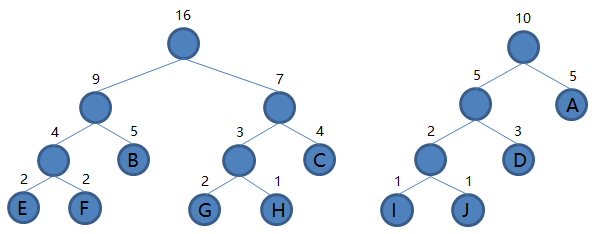
9.从集合里取出根结点权值最小的两棵树 EFBGHC 和 IJDA 组成新的二叉树 EFBGHCIJDA,根结点权值为 16 + 10 = 26,将二叉树 EFBGHCIJDA 加入集合,把 EFBGHC 和 IJDA 从集合里删除,如下图。
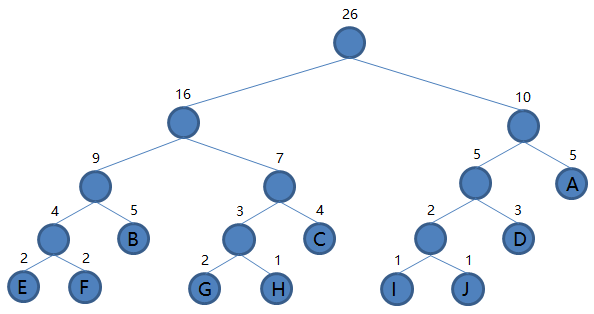
到这里我们发现集合里就剩一棵二叉树了,那么编码结束,最后这棵二叉树就是我们要得到的哈夫曼树。接下来我们规定非叶子结点的结点,到左子树的路径记为 0,到右子树的路径记为 1,如下图:
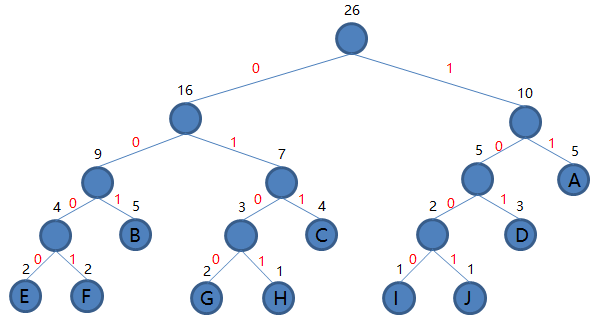
根结点到每个叶子结点的路径便是其对应字母的编码了,于是我们可以得到:
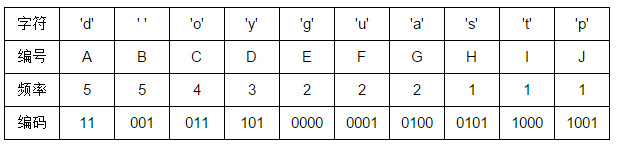
下面我们来算一下哈夫曼树的带权路径长度 WPL,也就是每个叶子到根的距离乘以叶子权值结果之和。
WPL = 5 * 2 + 5 * 3 + 4 * 3 + 3 * 3 + 2 * 4 + 2 * 4 + 2 * 4 + 1 * 4 + 1 * 4 + 1 * 4 = 82。
我们来算下如果直接存储字符串需要多少个比特,我们知道一个字符占一个字节,一个字节占 8 个比特,所以一共需要 8 * 26 = 208 个比特。我们再来看看哈夫曼编码需要多少个比特,我们可以发现 WPL 也就是编码后原来字符串所占的比特总长度 82。显然,哈夫曼编码把原数据压缩了好多,而且没有损失。
当然WPL也可以用节点权值相加所得。
WPL = 16 + 10 + 9 + 7 + 5 + 5 + 4 + 5 + 3 + 4 + 2 + 3 + 2 + 2 + 2 + 1 + 1 + 1 = 82。
这也可以用优先队列来实现。

1 #include<iostream> 2 using namespace std; 3 class Heap { 4 private: 5 int *data, size; 6 public: 7 Heap(int length_input) { 8 data = new int[length_input]; 9 size = 0; 10 } 11 ~Heap() { 12 delete[] data; 13 } 14 void push(int value) { 15 data[size] = value; 16 int current = size; 17 int father = (current - 1) / 2; 18 while (data[current] < data[father]) { 19 swap(data[current], data[father]); 20 current = father; 21 father = (current - 1) / 2; 22 } 23 size++; 24 } 25 int top() { 26 return data[0]; 27 } 28 void update(int pos, int n) { 29 int lchild = 2 * pos + 1, rchild = 2 * pos + 2; 30 int max_value = pos; 31 if (lchild < n && data[lchild] < data[max_value]) { 32 max_value = lchild; 33 } 34 if (rchild < n && data[rchild] < data[max_value]) { 35 max_value = rchild; 36 } 37 if (max_value != pos) { 38 swap(data[pos], data[max_value]); 39 update(max_value, n); 40 } 41 } 42 void pop() { 43 swap(data[0], data[size - 1]); 44 size--; 45 update(0, size); 46 } 47 int heap_size() { 48 return size; 49 } 50 }; 51 int main() { 52 int n, value, ans = 0; 53 cin >> n; 54 Heap heap(n); 55 for (int i = 1; i <= n; ++i) { 56 cin >> value; 57 heap.push(value); 58 } 59 if (n == 1) { 60 ans += heap.top(); 61 } 62 while (heap.heap_size() > 1) { 63 int a = heap.top(); 64 heap.pop(); 65 int b = heap.top(); 66 heap.pop(); 67 ans += a + b; 68 heap.push(a+b); 69 } 70 cout << ans << endl; 71 return 0; 72 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号