MR素性检测算法

　　转载地址：　http://m.blog.csdn.net/blog/spirtsong/38273187

　　素数是除了自身和1以外，没有其它素数因子的自然数。自从欧几里得证明了有无穷个素数以后，人们就企图寻找一个可以构造所有素数的公式，寻找判定一个自然数是不是素数的方法。因为素数的地位非常重要。

　　鉴别一个自然数是素数还是合数，这个问题在中世纪就引起人们注意，当时人们试图寻找质数公式，到了高斯时代，基本上确认了简单的质数公式是不存在的，因此，高斯认为对素性判定是一个相当困难的问题。从此以后，这个问题吸引了大批数学家。素性判断算法可分为两大类，确定性算法及随机算法。前者可给出确定的结果但通常较慢，后者则反之。

　　这里主要讲米勒拉宾算法，最后提供c++实现代码。

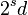　　要测试 $N$ 是否为素数，首先将 $N-1$ 分解为 $2^s d$ 。在每次测试开始时，先随机选一个介于 $[1, N-1]$ 的整数 $a$ ，之后如果对所有的 $r \in [0, s-1]$ ，若 $a^d \mod N \neq 1$ 且 $a^{2^{r}d} \mod N \neq -1$ ，则 N 是合数。否则， $N$ 有 $3/4$ 的概率为素数。

　　Miller- Rabin算法随机生成底数a，进行多次调用函数进行测试，Miller-Rabin检测也存在伪素数的问题，但是与费马检测不同，MR检测的正确概率不依赖被检测数p，而仅依赖于检测次数。已经证明，如果一个数p为合数，那么Miller-Rabin检测的证据数量不少于比其小的正整数的3/4，换言之，k次检测后得到错误结果的概率为(1/4)^k。我们在实际应用中一般可以测试15~20次。

 1 #include <iostream>
 2 #include <cmath>
 3 using namespace std;
 4 
 5 long long qpow(int a,int b,int r)//快速幂
 6 {
 7     long long ans=1,buff=a;
 8     while(b)
 9     {
10         if(b&1)ans=(ans*buff)%r;
11         buff=(buff*buff)%r;
12         b>>=1;
13     }
14     return ans;
15 }
16 bool Miller_Rabbin(int n,int a)//米勒拉宾素数测试
17 {
18     int r=0,s=n-1,j;
19     if(!(n%a))
20         return false;
21     while(!(s&1)){
22         s>>=1;
23         r++;
24     }
25     long long k=qpow(a,s,n);
26     if(k==1)
27         return true;
28     for(j=0;j<r;j++,k=k*k%n)
29         if(k==n-1)
30             return true;
31     return false;
32 }
33 bool IsPrime(int n)//判断是否是素数
34 {
35     int tab[]={2,3,5,7};
36     for(int i=0;i<4;i++)
37     {
38         if(n==tab[i])
39             return true;
40         if(!Miller_Rabbin(n,tab[i]))
41             return false;
42     }
43     return true;
44 }
45 int main()
46 {
47     long long n;
48     while(1)
49     {
50        cin >> n;
51     cout << IsPrime(n)<< endl;
52     }
53 
54     return 0;
55 }

在一次检验中，该算法出错的可能顶多是四分之一。如果我们独立地和随机地选择 a 进行重复检验，一旦此算法报告 n 是合数，我们就可以确信 n 肯定不是素数。但如果此算法重复检验 25 次报告都报告说 n 可能是素数，则我们可以说 n “几乎肯定是素数”。因为这样一个 25 次的检验过程给出关于它的输入的错误信息的概率小于 (1/4)²⁵。这种机会小于 10¹⁵ 分之一。即使我们以这样一个过程验证了十亿个不同的素数，预料出错的概率仍将小于百万分之一。因此如果真出了错，与其说此算法重复地猜测错，倒不如说由于硬件的失灵或宇宙射线的原因，我们的计算机在它的计算中丢了一位。这样的概率性算法使我们对传统的可靠性标准提出一个问号：我们是否真正需要有素性的严格证明。(以上文字引用自 Donald E.Knuth 所著的《计算机程序设计艺术第2卷半数值算法(第3版)》第 359 页“4.5.4 分解素因子”中的“算法P(概率素性检验)”后面的说明)

posted @ 2015-10-29 17:50 clairvoyant 阅读(3825) 评论(1) 编辑收藏举报

刷新页面返回顶部

clairvoyant

MR素性检测算法

公告