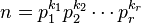10.2计数与概率基础
1.加法原理:
做一件事有n种方法,第i个步骤有pi种方案。则一共同拥有p1+p2+……+pn种方案
2.乘法原理:
做一件事。完毕它须要分成n个步骤,做第一 步有m1种不同的方法。做第二步有m2不同的方法。……。做第n步有mn不同的方法。那么完毕这件事共同拥有 N=m1×m2×m3×…×mn 种不同的方法。 和加法原理是数学概率方面的基本原理。
3.容斥原理:
在计数时。必须注意无一反复,无一遗漏。
为了使重叠部分不被反复计算。人们研究出一种新的计数方法。这样的方法的基本思想是:先不考虑重叠的情况,把包括于某内容中的全部对象的数目先计算出来,然后再把计数时反复计算的数目排斥出去,使得计算的结果既无遗漏又无反复,这样的计数的方法称为容斥原理。
A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C
4.有反复元素的全排列:
【描写叙述】有k个元素。第i个元素有ni个。求全排列的个数
【分析】
5.可反复选择的组合:
【描写叙述】
【分析】
6.杨辉三角和二项式定理:
杨辉三角
7.数论中的计数问题:
①约数的个数:
②小于n且与n互素的整数个数(欧拉函数):
【描写叙述】给出正整数n的唯一分解式n = p1^a1*p2^a2*p3^a3*p4^a4*……pk^ak,求小于n的数中与n互素的个数
【分析】对于素数p来说。“与p互素”和“不是p的倍数”等价。利用容斥原理,n - “p1,p2,……,pk的倍数的个数” + “同一时候是两个素因子的倍数”的个数 - “同一时候是三个素因子的倍数”…………………………
【唯一分解式的求得】
(1)利用试除法依次推断√n内全部素数是否有n的因子(须要打素数表)
(2)在√n每次找到一个素因子把他除干净(巧用break)。自己尽管用了非常长时间这个思路,可是还是LRJ的代码写得好:
int m = (int)sqrt(m + 0.5);
int ans = n;
for(int i = 2;i <= m;i++)
if(n % i == 0) //寻找素因子
{
ans = ans / i * (i - 1);
while(n % i == 0) n /= i; //抓住一个素因子就除尽它
}
if(n > 1) ans = ans / n * (n - 1);
【欧拉函数】(咋变形的?)
若
则。
当中是使得
整除
的最大整数
(这里
)。
【代码】求1~n中全部数的欧拉phi函数值
//相似于筛选法求素数
int n,phi[100005];cin>>n;
memset(phi,0,sizeof(phi));
phi[1] = 1;
for(int i = 2;i <= n;i++)
if(!phi[i])
for(int j = i;j <= n;j += i)
{
if(!phi[j]) phi[j] = j;
phi[j] = phi[j] / i * (i - 1);
}
for(int i = 1;i <= n;i++) printf("%d\n",phi[i]);