LDA实现
topic model本质上就一个套路,在doc-word user-url user-doc等关系中增加topic层,扩充为2层结构,一方面可以降维,另一方面挖掘深层次的关系,用户doc word user url的聚类。
LDA的理论知识不介绍太多,基本就讲了原理以及推导两个内容,原理比较简单,推导过程貌似很简单,就一个变分加上一些参数估计的方法就搞定了,但是具体的细节还没明白,以后慢慢研究。
简单介绍下基本原理以及有意义的几个公式:
plsa作为topic-model ,每篇文档对应一系列topics,每个topic对应一批terms,有如下问题:
1.每篇文档及其在topic上的分布都是模型参数,也就是模型参数随着文档的数目增加而增加,这样容易导致overfitting
2.对于new doc,如何确定其topic 分布
LDA解决这个问题,没必要把每个doc-topic分布作为模型参数,为doc-topic分布增加一个先验概率,限制整体上文档的topic分布,具体先验分布的作用,之前已经介绍过。
doc-topic分布服从多项分布,狄利克雷分布是其共轭先验。
这样参数的个数就变成K + N*K, N为词个数,K为topic个数,与文档个数无关。
如果我想知道一个文档的topic分布怎么办?下面介绍下train以及predic的方法。
作者采用了varitional inference进行推导,过程就免了,列出来几个重要的公式:
论文中几个重要公式:
概率模型:
D 表示文档集合,最后就是保证P(D|α,β)最大。![]()
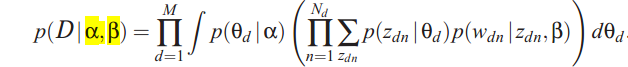
phi的迭代公式,表示文档中单词n在topic i上的分布:
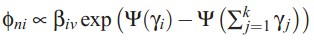
gamma的迭代公式,文档在topic上的分布
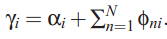
Beta的迭代公式,model中topic-word分布:
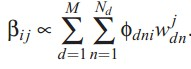
alpha的迭代公式,model中文档-topic分布的先验参数,利用梯度下降法即可求解:
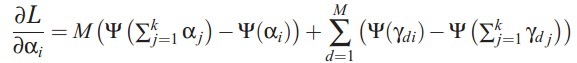
LDA最核心的迭代公式,针对每一篇文档,计算每个词的topic分布,从而计算文档的topic分布:

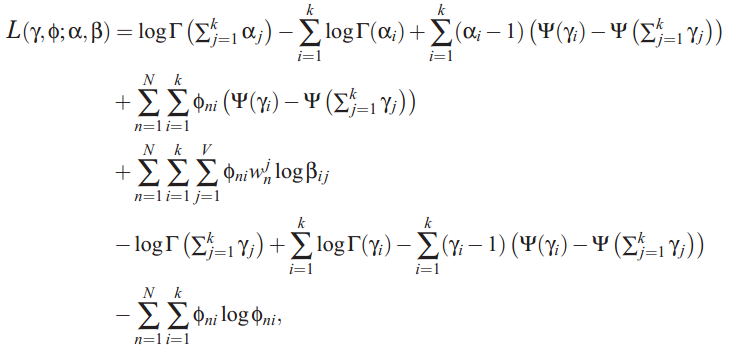
基本逻辑:
1.初始模型参数,开始迭代,执行2,3,4,直至收敛
2.针对每一篇文档,初始gamma以及phi参数,迭代该参数,直至收敛
2.1.计算文档中每个单词在topic上的分布,利用model中beta以及文档-topic分布(2.2)
2.2.计算文档-topic分布,利用模型参数alpha以及word-topic分布(2.1结果)
3.update模型参数beta,利用word-topic分布。
4.update模型参数alpha,利用2.2的结果gamma
源码介绍
模型参数:
var_gamma:文档-topic分布,每篇文档都会计算其topic分布
phi: word-topic分布,针对每篇文档,计算文档中每个word的topic分布
lda_mode: lad的模型参数,里面包括beta以及alpha
lda_suffstats: 记录统计信息,比如每个topic上每个word出现的次数,这是为了计算lda_model而存在
corpus: 全部文档信息
document: 文档的具体信息,包括word信息
corpus_initialize_ss:初始化 ss,随机选择一些文档,利用文档词信息update ss 里面topic上term的频度
| for (k = 0; k < num_topics; k++) { for (i = 0; i < NUM_INIT; i++) { d = floor(myrand() * c->num_docs); printf("initialized with document %d\n", d); doc = &(c->docs[d]); for (n = 0; n < doc->length; n++) { ss->class_word[k][doc->words[n]] += doc->counts[n]; } } for (n = 0; n < model->num_terms; n++) { ss->class_word[k][n] += 1.0; ss->class_total[k] = ss->class_total[k] + ss->class_word[k][n]; } } |
random_initialize_ss:随机选取一些值初始化ss
run_em:执行EM算法,针对每篇文档,利用其单词以及初始化的β和α信息 更新模型,直至收敛。
该函数是一个框架性质的,具体的见下。
| void run_em(char* start, char* directory, corpus* corpus) { int d, n; lda_model *model = NULL; double **var_gamma, **phi; // allocate variational parameters var_gamma = malloc(sizeof(double*)*(corpus->num_docs)); for (d = 0; d < corpus->num_docs; d++) var_gamma[d] = malloc(sizeof(double) * NTOPICS); int max_length = max_corpus_length(corpus); phi = malloc(sizeof(double*)*max_length); for (n = 0; n < max_length; n++) phi[n] = malloc(sizeof(double) * NTOPICS); // initialize model char filename[100]; lda_suffstats* ss = NULL; if (strcmp(start, "seeded")==0) { model = new_lda_model(corpus->num_terms, NTOPICS); ss = new_lda_suffstats(model); corpus_initialize_ss(ss, model, corpus); lda_mle(model, ss, 0); model->alpha = INITIAL_ALPHA; } else if (strcmp(start, "random")==0) { model = new_lda_model(corpus->num_terms, NTOPICS); ss = new_lda_suffstats(model); random_initialize_ss(ss, model); lda_mle(model, ss, 0); model->alpha = INITIAL_ALPHA; } else { model = load_lda_model(start); ss = new_lda_suffstats(model); } sprintf(filename,"%s/000",directory); save_lda_model(model, filename); // run expectation maximization int i = 0; double likelihood, likelihood_old = 0, converged = 1; sprintf(filename, "%s/likelihood.dat", directory); FILE* likelihood_file = fopen(filename, "w"); while (((converged < 0) || (converged > EM_CONVERGED) || (i <= 2)) && (i <= EM_MAX_ITER)) { i++; likelihood = 0; zero_initialize_ss(ss, model); // e-step //这里是核心,针对每篇文档计算相关模型参数 for (d = 0; d < corpus->num_docs; d++) { likelihood += doc_e_step(&(corpus->docs[d]), var_gamma[d], phi, model, ss); } // m-step lda_mle(model, ss, ESTIMATE_ALPHA); // check for convergence converged = (likelihood_old - likelihood) / (likelihood_old); if (converged < 0) VAR_MAX_ITER = VAR_MAX_ITER * 2; likelihood_old = likelihood; |
doc_e_step:执行EM中的E-step,干了两件事情
1.基于文档的单词,update φ以及γ,得到doc-topic 分布以及 word-topic分布(lda_inference)
2.利用γ信息,更新α,这里的α只有一个参数,所以计算方式不同。
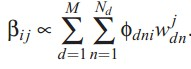
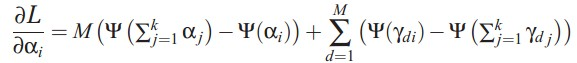
本来应该是αi = αi + ![]() ,但是实际α只有一个,所以作者通过在所有topic上的分布计算出α。
,但是实际α只有一个,所以作者通过在所有topic上的分布计算出α。
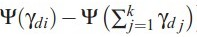 ,但是实际α只有一个,所以作者通过在所有topic上的分布计算出α。
,但是实际α只有一个,所以作者通过在所有topic上的分布计算出α。每篇文档迭代一次,遍历完所有文档后,就计算出最后的α。
| double doc_e_step(document* doc, double* gamma, double** phi, lda_model* model, lda_suffstats* ss) { double likelihood; int n, k; // posterior inference likelihood = lda_inference(doc, model, gamma, phi); // update sufficient statistics double gamma_sum = 0; for (k = 0; k < model->num_topics; k++) { gamma_sum += gamma[k]; ss->alpha_suffstats += digamma(gamma[k]); } ss->alpha_suffstats -= model->num_topics * digamma(gamma_sum); for (n = 0; n < doc->length; n++) { for (k = 0; k < model->num_topics; k++) { ss->class_word[k][doc->words[n]] += doc->counts[n]*phi[n][k]; ss->class_total[k] += doc->counts[n]*phi[n][k]; } } ss->num_docs = ss->num_docs + 1; return(likelihood); } |
lad_inference:这是最核心的code,基于每个doc,计算对应γ和φ,也就是doc-topic以及word-topic分布。也就是如下代码:
利用topic个数以及word个数,初始化γ以及φ。
严格实现这个过程,工程做了优化,对φ取了对数logφ,这样降低计算复杂度,同时利用log_sum接口,计算log(φ1) log(φ2)...log(φk)计算出log(φ1+φ2.....+φk),这样利用(logφ1)-log(φ1+φ2.....+φk)即可完成归一化。
利用:

解释下代码:
针对文档中的每一个词 n:
针对每个topic i:
单词n在topic i上的分布为:φni = topic i在word n上的分布 × exp(Digamma(该文档在toic i上的分布))
归一化 φni
文档在topic上的分布γi = 其先验分布αi + 文档内所有词在topic i上的分布值和
lda-infernce,不只是在train的时候使用,对于一片新的文档,同样是通过该函数/方法计算文档在tpoic上的分布,只依赖于模型参数α以及β
利用:
| double lda_inference(document* doc, lda_model* model, double* var_gamma, double** phi) { double converged = 1; double phisum = 0, likelihood = 0; double likelihood_old = 0, oldphi[model->num_topics]; int k, n, var_iter; double digamma_gam[model->num_topics]; // compute posterior dirichlet //init gama and php for (k = 0; k < model->num_topics; k++) { //初始化 γ以及φ var_gamma[k] = model->alpha + (doc->total/((double) model->num_topics)); digamma_gam[k] = digamma(var_gamma[k]); for (n = 0; n < doc->length; n++) phi[n][k] = 1.0/model->num_topics; } var_iter = 0; while ((converged > VAR_CONVERGED) && ((var_iter < VAR_MAX_ITER) || (VAR_MAX_ITER == -1))) { var_iter++; for (n = 0; n < doc->length; n++) { phisum = 0; for (k = 0; k < model->num_topics; k++) { oldphi[k] = phi[n][k]; //对于每个word,更新对应的topic,也就是公式中 phi[n][k] = digamma_gam[k] + model->log_prob_w[k][doc->words[n]]; if (k > 0) //为归一化做准备,通过log(a) +log(b)计算log(a+b) phisum = log_sum(phisum, phi[n][k]); else phisum = phi[n][k]; // note, phi is in log space } for (k = 0; k < model->num_topics; k++) { phi[n][k] = exp(phi[n][k] - phisum);//归一化 //update γ,这里面没有用到α,原始公式不同 var_gamma[k] =var_gamma[k] + doc->counts[n]*(phi[n][k] - oldphi[k]); // !!! a lot of extra digamma's here because of how we're computing it // !!! but its more automatically updated too. digamma_gam[k] = digamma(var_gamma[k]); printf("%d:%d: gmama: %f php: %f\n", n, k, var_gmama[k], php[n][k]); } } //计算似然结果,观察是否收敛,计算采用公式 likelihood = compute_likelihood(doc, model, phi, var_gamma); assert(!isnan(likelihood)); converged = (likelihood_old - likelihood) / likelihood_old; likelihood_old = likelihood; // printf("[LDA INF] %8.5f %1.3e\n", likelihood, converged); } return(likelihood); } |
compute likehood:这个函数实现的是blei LDA 公式15,也就是定义的似然函数,比较复杂,但是严格按照这个实现。
需要注意的是,blei的代码,k个α值相同,计算时 包含α的计算进行了简化。
利用:
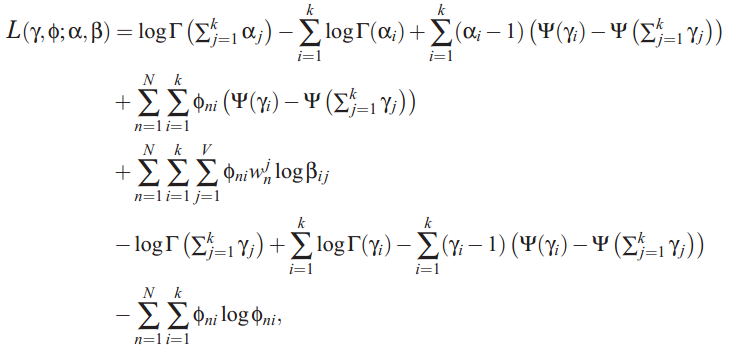
| double compute_likelihood(document* doc, lda_model* model, double** phi, double* var_gamma) { double likelihood = 0, digsum = 0, var_gamma_sum = 0, dig[model->num_topics]; int k, n; for (k = 0; k < model->num_topics; k++) { dig[k] = digamma(var_gamma[k]); var_gamma_sum += var_gamma[k]; } digsum = digamma(var_gamma_sum); lgamma(α*k) - k*lgamma(alpha) likelihood = lgamma(model->alpha * model -> num_topics) - model -> num_topics * lgamma(model->alpha) - (lgamma(var_gamma_sum)); for (k = 0; k < model->num_topics; k++) { likelihood += (model->alpha - 1)*(dig[k] - digsum) + lgamma(var_gamma[k]) - (var_gamma[k] - 1)*(dig[k] - digsum); for (n = 0; n < doc->length; n++) { if (phi[n][k] > 0) { likelihood += doc->counts[n]* (phi[n][k]*((dig[k] - digsum) - log(phi[n][k]) + model->log_prob_w[k][doc->words[n]])); } } } return(likelihood); } |
lda_mle:针对每个文档执行do_e_step后,更新了ss,也就是计算模型所需要数据,topic-word对的次数
void lda_mle(lda_model* model, lda_suffstats* ss, int estimate_alpha){
int k; int w;
for (k = 0; k < model->num_topics; k++)
{
for (w = 0; w < model->num_terms; w++)
{
if (ss->class_word[k][w] > 0)
{
model->log_prob_w[k][w] =
log(ss->class_word[k][w]) -
log(ss->class_total[k]);
}
else
model->log_prob_w[k][w] = -100;
}
}
if (estimate_alpha == 1)
{
model->alpha = opt_alpha(ss->alpha_suffstats,
ss->num_docs,
model->num_topics);
printf("new alpha = %5.5f\n", model->alpha);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号