动态规划之最长公共子序列
问题引入
有两个串S1和S2,寻找第三个串S3,要求S3的所有内容都出现在S1和S2中,且在三个串中出现的顺序相同,但在S1和S2中不要求连续出现。
S3称为S1和S2的最长公共子序列(LCS)。
求解方案
在求X=<x1,x2,x3,...,xm>和Y=<y1,y2,y3,...yn>的一个Lcs时,需要求解一个或两个子问题:
1.如果xm = yn,就应该求解xm-1和yn-1的一个LCS。将xm和yn追加到这个Lcs上,就得到X和Y的Lcs
2.如果xm!=yn,则要求解两个子问题:求Xm-1和Y的一个Lcs与X和Yn-1的一个Lcs。两个Lcs中的较长者即为X和Y的一个Lcs。
很明显,上述求解方式满足动态规划的两个条件:最优子结构和子问题重叠
自底向上的动态规划求解
public class LongestCommonSubsequence {
public static void main(String[] args) {
String X = "ABCBDAB";
String Y = "BDCABA";
char[][] b = lcs(X,Y);
char[] x = X.toCharArray();
printLcs(b,x,X.length(),Y.length());
}
//动态规划自底向上计算
static char[][] lcs(String X, String Y){
char[] x = X.toCharArray();
char[] y = Y.toCharArray();
int m = x.length, n = y.length;
char[][] b = new char[m][n];
int[][] c = new int[m+1][n+1];
//初始化c的第一行和第一列为0
for (int i = 0;i <= m;i++){
c[i][0] = 0;
}
for (int j = 0;j <= n;j++){
c[0][j] = 0;
}
for (int i = 1;i <= m;i++){
for (int j = 1;j <=n;j++){
//如果比较结果相等,则c[i][j]为x[i-1]和y[j-1]最长公共子序列长度+1
if (x[i-1] == y[j-1]){
c[i][j] = c[i-1][j-1]+1;
b[i-1][j-1] = '↖';
//结果不等,则c[i][j]取 x[i]与y[j-1]的最长公共子序列 和 x[i-1]与y[j]的最长公共子序列 中的较大者
}else if (c[i-1][j] >= c[i][j-1]){
c[i][j] = c[i-1][j];
b[i-1][j-1] = '↑';
}else {
c[i][j] = c[i][j-1];
b[i-1][j-1] = '←';
}
}
}
for (int i = 0;i < m+1;i++){
for (int j = 0;j < n+1;j++){
System.out.print(c[i][j]);
}
System.out.println();
}
for (int i = 0;i < m;i++){
for (int j = 0;j < n;j++){
System.out.print(b[i][j]);
}
System.out.println();
}
return b;
}
//b为lcs得到的二维数组;x为其中一个字符串(转换为字符数组);m,n分别为两个字符串的长度
static void printLcs(char[][] b,char[] x,int m,int n){
if (m == 0 || n == 0){
return;
}
//b[m-1][n-1]=='↖'对应的是x[m-1]和y[n-1]相等,于是递归调用printLcs从b[m-2][n-2]判断
if (b[m-1][n-1] == '↖'){
printLcs(b,x,m-1,n-1);
System.out.print(x[m-1]);
//x[m-1]和y[n-1]不等,递归调用printLcs从b[m-2][n-1]判断,因为b[m-1][n-1] == '↑'表示
//x[i]与y[j-1]的最长公共子序列 和 x[i-1]与y[j]的最长公共子序列 中的较大者为后者
}else if (b[m-1][n-1] == '↑'){
printLcs(b,x,m-1,n);
//x[m-1]和y[n-1]不等,递归调用printLcs从b[m-1][n-2]判断,因为b[m-1][n-1] == '←'表示
//x[i]与y[j-1]的最长公共子序列 和 x[i-1]与y[j]的最长公共子序列 中的较大者为前者
}else {
printLcs(b, x, m, n-1);
}
}
}

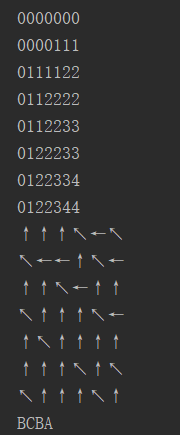
运行结果如下: