红黑树简介

红黑树

性质

红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位表示颜色，可以是RED或BLACK。通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似于平衡的。

一棵红黑树要满足以下红黑性质：

1.节点是红色或黑色。

2.根节点是黑色。

3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

下面是一棵典型的红黑树：

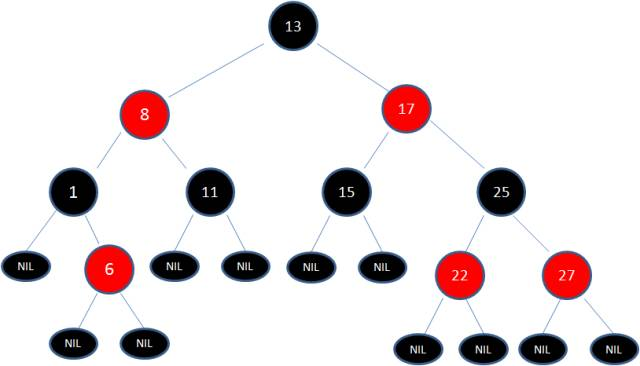
定义：从某个节点出发(不含该节点)到达一个叶节点的任意一条简单路径上的黑色节点个数称为该节点的黑高。（NIL的黑高为0，即不含叶子结点）

当对红黑树进行插入，删除等操作后，为了保证红黑树还是红黑树，需要进行调整。调整有两种方式：变色和旋转

变色

为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。

下图所表示的是红黑树的一部分，需要注意节点25并非根节点。因为节点21和节点22连续出现了红色，不符合规则4，所以把节点22从红色变成黑色：

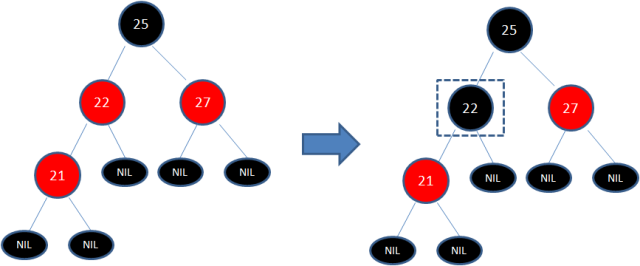
但这样并不算完，因为凭空多出的黑色节点打破了规则5，所以发生连锁反应，需要继续把节点25从黑色变成红色：

此时仍然没有结束，因为节点25和节点27又形成了两个连续的红色节点，需要继续把节点27从红色变成黑色：

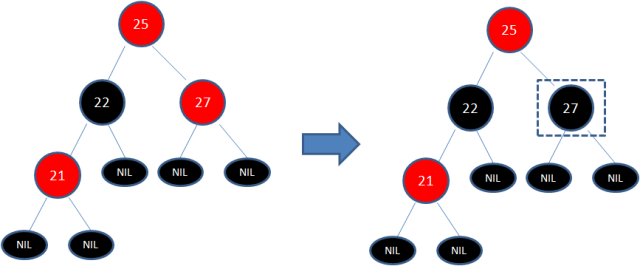
旋转

左旋

逆时针旋转红黑树的两个节点

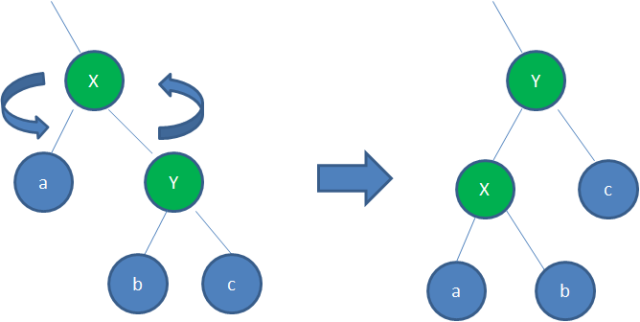
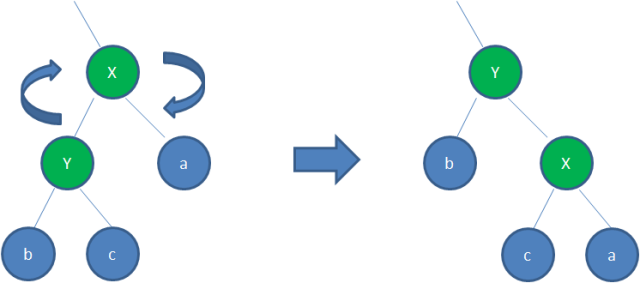
右旋

顺时针旋转红黑树的两个节点

当进行一次插入或删除操作后，往往需要多步变色+旋转操作