非比较排序

当脱离了比较排序模型的时候，(nlgn)这一下界就不再适用。

1.计数排序

计数排序：n个输入元素的每一个都是在0到k之间的整数（k为某个整数）。

1.假设输入数组是A[1..n],还需要两个数组：B[1..n]存放排序的输出，C[0..k]提供临时存储空间

2.C[i]中存放等于 i 的元素的个数，i=0,1，，k

3.通过相加计算确定有多少元素是小于等于i的

4.把每个元素A[i]放到数组B正确的位置

 

#include <iostream>
#include <vector>
using namespace std;
 
void CountSort(vector<int> &arr, int maxVal) {
    int len = arr.size();
    if (len < 1)
        return;
    vector<int> count(maxVal+1, 0);
    vector<int> tmp(arr);
    for (auto x : arr)
        count[x]++;
    for (int i = 1; i <= maxVal; ++i)
        count[i] += count[i - 1];
    for (int i = len - 1; i >= 0; --i) {
        arr[count[tmp[i]] - 1] = tmp[i];
        count[tmp[i]]--;                //注意这里要减1
    }
}
 
int main()
{
    vector<int> arr = { 1,5,3,7,6,2,8,9,4,3,3 };
    int maxVal = 9;
    CountSort(arr,maxVal);
    for (auto x : arr)
        cout << x << " ";
    cout << endl;
    return 0;
}

 

 

2.桶排序

计数排序的升级版：计数排序计算等于某个值的元素的个数，桶排序则是计算值在

某区间的元素的个数，每个桶就是一个区间，分好后通过其他排序方法进行桶内排序。

当待排序元素取值范围过大或者不是整数时，就不能使用计数排序，可使用桶排序。

 

和计数排序的比较

1.计数排序

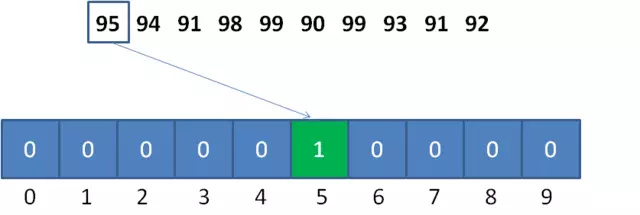
计数排序需要根据原始数列的取值范围，创建一个统计数组，用来统计原始数列中每一个可能的整数值所出现的次数。

原始数列中的整数值，和统计数组的下标是一一对应的，以数列的最小值作为偏移量。比如原始数列的最小值是90，

那么整数95对应的统计数组下标就是 95-90 = 5。

 

2.桶排序

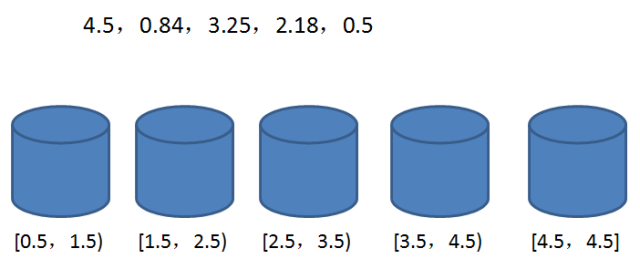
每一个桶（bucket）代表一个区间范围，里面可以承载一个或多个元素。桶排序的第一步，就是创建这些桶，确定每一个桶的区间范围：

 具体建立多少个桶，如何确定桶的区间范围，有很多不同的方式。

 

当待排序元素在某个区间内分布均匀时，桶排序效率很高，但如果分布很不均匀，桶排序意义不大。

 

 

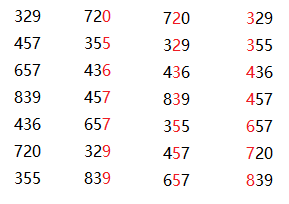
3.基数排序

基数排序是先按最低位进行排序，依次向高位排。

前提是对每一位的排序必须是稳定的，例如可以基于计数排序进行基数排序。