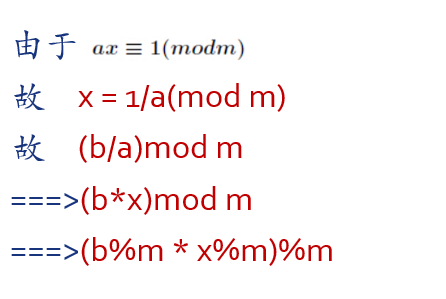牛客Wannafly挑战赛13-BJxc军训-费马小定理、分式取模、快速幂

参考：https://blog.csdn.net/qq_40513946/article/details/79839320

传送门：https://www.nowcoder.com/acm/contest/80/B

题意：输入n，m，求 (n*n-m)/n*n 在 取模998244353下的解；

思路：

 

题目给出的条件是费马小定理，那么可以知道 x负一次方等于x的（p-2）次mod（MOD）  ，所以只要快速幂求出x的（p-2） 就可以了，时间复杂度 O（logMod)。

                

ac代码：

#include <iostream>
using namespace std;

typedef long long ll;
const int md = 998244353;
ll fpow(ll a,ll n)//快速幂
{
    ll res = 1;
    while(n)
    {
        if(n&1)
            res = res*a%md;
        a = a*a%md;
        n>>=1;
    }
    return res;
}
int main(){
    int n,m;
    cin>>n>>m;
    ll t = n*n-m;
    ll ans = t%md*(fpow( n*n , md-2)%md)%md;
    cout<<ans<<endl;

    return 0;
}