洛谷P1240-诸侯安置+递推非搜索

诸侯安置

这道题是一题递推题，一开始自己不知道，用了搜索，只过了三个样例；

 

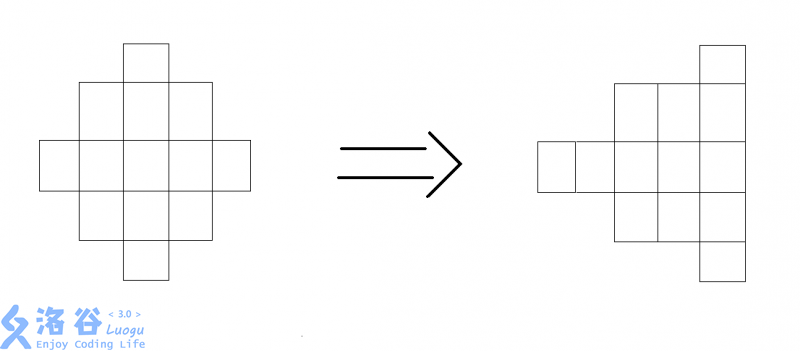
两两相同的合并，

成 1，1，3，3，5，5........n*2-1;

然后我们会容易发现一种不同与搜索的动态规划做法.

f[i,j]:=f[i,j]+f[k,j-1]*(Len[i]-(j-1)) [j-1<=k<=i-1]

1.f[i,j]表示前i列放置j个的方案，且第j个放在第i列上，

2.前面f[k,j-1]个都需要累加上来，举一个说明为什么需要累加：对于前4排放置2个的情况(平移后的)，2个即可以放在第一列和第三列，也可以放在第一列和第四列，所以需要把这些分布在不同列的情况累加上来。

3.乘(Len[i]-(j-1))是因为前面k列放了j-1个棋子了，然后每行只能放一个棋子，所以第j个棋子在第i列可以放的情况就是Len[i]-(j-1),len[i]是第i列有多少行，程序中是l[i];

 

下面是ac代码

#include <cstdio>

using namespace std;

int l[207],dp[200+7][200+7];
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    if(k==0){printf("1\n");return 0;}
    if(k>2*n-1){printf("0\n");return 0;}
    int t = 1;
    for(int i=1;i<=n;i++)
    {
          l[2*i-1]=l[2*i]=2*i-1;
    }
    dp[0][0]=1;
    for(int i=1;i<=2*n-1;i++)   //表示当前是第几行
    {
        for(int j=1;j<=i;j++) //可以通过找规律发现，f[i][j]其实是 （f[1~i-1][j]*剩余可放列数） 的总和
        {
            for(int u=j-1;u<i;u++)
                dp[i][j]=(dp[i][j]+dp[u][j-1]*(l[i]-j+1))%504;
        }
    }
    int ans = 0;
    for(int i=k;i<=2*n-1;i++)   //注意ans一定是f[k~2*n-1][k]的总和
    {
        ans =(ans+dp[i][k])%504;
    }
    printf("%d\n",ans%504);
    return 0;
}