电磁学14.自感与RL电路

自感L

在电路中通入电流，就制造了磁场，如果电流在变化，磁场也会变化，而电路中感性元件会产生感生电动势来抵抗这种变化。

这种效果我们用 "自感" 表示。自感越大，抵抗力越大，消除（达到电路稳态）时间越长。

如果在交流中，自感时刻在抵抗电流的变化，所以会让电流“滞后”于电压的变化。

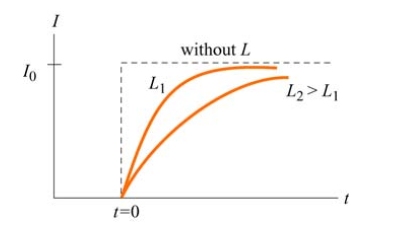
由电流产生的磁通量总是和电流大小成正比，我们将比例常数定义为 "自感 \(L\) （self-inductance）“。单位是”亨利 \(H\)“ .

\[\phi _B =I L \]

而法拉第电磁感应定律告诉我们，感应电动势大小为（注意符号——楞次定律的含义）：

\[E=-\frac{\text{d$\phi $}_B}{\text{dt}} \]

所以

\[E=-L\frac{\text{d$I $}}{\text{dt}} \]

自感只和几何形状有关。

比如在螺线管中，假设外部磁感应强度为0.

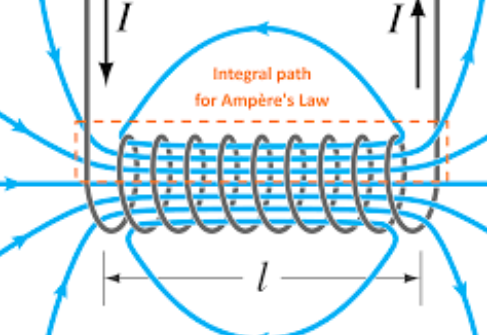
我们在安培环路定理计算过，内部磁感应强度为

\[B= \mu _0 I \frac{N}{l} \]

磁通量 （N匝相当于有N个圆面 \(\pi r^2\) ——想象把螺线管沉入肥皂水后，她所连上的开曲面，磁场会穿过圆面 N 次，磁通量乘以N倍） 为

\[\begin{align} \phi _B &=N \pi r^2 B\\ &= \pi r^2 \frac{N^2 }{l}\mu _0 I\\ &= LI \end{align} \]

故

\[L= \pi r^2 \frac{ N^2}{l} \mu _0 \]

RL电路

零状态响应

如图，在 \(t_0\) 时刻，回路电流为0，此时闭合开关，电流变化，磁场变化。

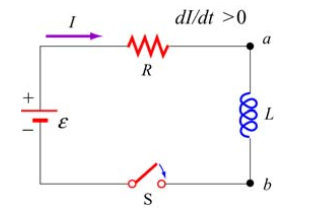
从电源负极开始，由基尔霍夫电压定律可得

\[\epsilon-\text{IR}-|\epsilon _L |=-\epsilon-\text{IR}-L\frac{\text{d$I $}}{\text{dt}} =0 \]

求解电流 \(I\) ,显然这是一阶微分方程。

解为

\[I(t)=\frac{\epsilon }{R} (1-e^{-\frac{R }{L}t}) \]

\(\frac{\epsilon }{R}\) 为最后电路稳态时最大电流。

需要注意基尔霍夫电压定律用于集总参数模型，如果不是，只能用法拉第定律计算，纯自感是超导体（电阻为0），压降为0，电场为0.

\[\oint \overset{\rightharpoonup }{E} \overset{\rightharpoonup }{\text{dl}}=-\frac{\text{d$\phi $}_B}{\text{dt}}=-L\frac{\text{d$I $}}{\text{dt}} \]

分布参数电路，磁通量将在整个电路中变化。回路积分结果将是感应电动势。自感内电场为0，电阻为0。电阻电场为 \(IR\) .沿着电流方向，从电源的负极开始，我们可以列出方程：

\[-\epsilon+\text{IR}-0=-L\frac{\text{d$I $}}{\text{dt}} \]

结果一样。嗯，只是过程不一样。

电流和时间关系：

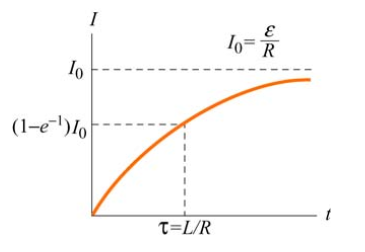
如果等待 \(\frac{L}{R}\) 秒，电流大约是最大值的 $63 $ % 。

如果等待 \(2\frac{L}{R}\) 秒，电流大约是最大值的 \(83\) % 。

零输入响应

如图，自感 L 初始通过 S1开关 充满电，最大电流为 \(I_{max}\) ，然后断开S1，闭合S2，在闭合S2的时刻规定为0时刻分析。

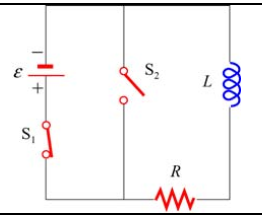
闭合S2，电流变化，磁场变化，楞次定律告诉我们，自感不喜欢电流变小的事实，她会反抗这种变化，所以我们可以猜测电流不会立刻消失。

在 \(t_0\) 时刻，电流还是最大值 \(I_{max}\) 。

同样的我们可以列出方程：

\[\text{IR}=-L\frac{\text{dI}}{\text{dt}} \]

解微分方程，得

\[I (t)=\frac{\epsilon }{R}e^{-\frac{R t}{L}} \]

画出图像为

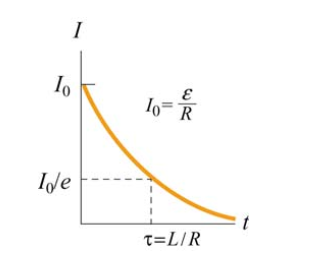
如果等待 \(\frac{L}{R}\) 秒，电流大约是最大值的 \(37\) % 。

我们发现，电阻到电流为0时，一直有热量产生，有电池时，电池提供能量；

没有电池时，磁场中的能量转换为电阻的热能形式散发，磁场提供能量。

基于这个观点，我们可以计算磁场能量密度。

磁场能量与磁场能量密度

磁场提供能量开始，到电流降为0，产生的热量为：

\[\begin{align} \int_0^{\infty } I^2 R \, dt &= I_{max}^2 R\int_0^{\infty }e^{-\frac{2R t}{L}} \, dt\\ &= I_{max}^2 R \frac{L}{2R}\\ &= \frac{LI_{max}^2}{2} \end{align} \]

而这就是磁场储存的能量。

我们可以把 \(I_{max}\) 替换为 \(I\) ，任意时刻流过螺线管的电流，磁场的能量随着电流变化而变化。

自感我们可以将其看成是螺线管，将 L 和 I 替换

\[B= \mu _0 I \frac{N}{l} \]

\[L= \pi r^2 \frac{ N^2}{l} \mu _0 \]

可得

\[\frac{LI^2}{2} = \frac{ B^2 }{2 \mu _0 } \pi r^2l \]

而 \(\pi r^2l\) 就是螺线管存在磁场处的体积（内部体积），因为我们假设外部磁场为0。

这是磁场总的能量。

故每立方米的能量为

\[\frac{ B^2 }{2 \mu _0 } \]

所以理论上来说，如果知道空间各处的磁感应强度，对全部空间积分，就可以计算出该空间磁场总能量。

早先我们计算电场能量密度。在电场情况下，她表示分配电荷到特定分布所做的功。

磁场的情况下，她表示让一个电流流过纯自感（电阻为0）必须做的功。做功是因为螺线管会抵抗电流的变化。

交流情况

用一个交流电源给LR串联电路供电，此时自感会时刻在抵抗，

交流电源电压为 $V=V_0 cos(\omega t) $

建立微分方程

\[V_0 cos(\omega t)-\text{IR}-L\frac{\text{d$I $}}{\text{dt}} =0 \]

解得电流为

\[I=\frac{V_0 }{\sqrt{R^2+\text{$\omega $L}^2}}\cos (\text{$\omega $t}-\Psi ) \]

其中

\[\tan (\Psi )=\frac{\text{$\omega $L}}{R} \]

可见，电流和驱动电压之间有相位滞后。相位角由这个式子决定。

如果 \(\Psi=90°\) ，那么电流滞后了 \(1/4\) 周期。

这是因为自感时刻在抵抗电流的变化，电流滞后驱动电压。

电流的最大值为

\[I_{max}=\frac{V_0 }{\sqrt{R^2+\text{$\omega $L}^2}} \]

因为cos项仅仅在±1之间振荡。

这里 \(\omega L\) 起到电阻的作用，叫做感抗。单位是欧姆。随着频率的变化而变化，频率越高，感抗越大，电流越低。在电压上可以起到衰减作用。

因为频率越高，电流变化率越大，EMF越大，电流越低。

直流电频率为0，故感抗为0.

对于相位角，自感或者频率越大，系统对电流变化的抵抗能力越强，能对电流有一个较大的延迟。因为是正切，所以图像上最大的相位偏差是90°（周期）。