电磁场12.EMF的产生与涡电流

产生EMF的三种方式

如下图，矩形的导电回路连接一个平面，长宽分别为 \(x,y\) ,一个均匀分布的磁场 \(B\) 穿过平面，且与平面的法向量的夹角为 \(\theta\) .

则磁通量定义为BdA在这个开曲面上的积分

\[\begin{align} \phi _B&=\underset{\text{open} \ \text{surface}}{\int } \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}}\\ &=x\ y\ B\ cos(\theta) \end{align} \]

根据法拉第定律，这个量对时间的导数，就是电动势 \(EMF\) 。

那么我们可以采用多种方式，

1. 取磁场的变化，即 \(\frac{\text{dB}}{\text{dt}}\)
2. 取面积的变化，即 \(\frac{\text{dA}}{\text{dt}}\)
3. 取夹角的变化，即 \(\frac{{d \theta}}{\text{dt}}\)

改变磁场产生EMF的方法我们已经讨论过，这里讨论夹角和面积。

改变夹角—发电机

如图，矩形的导电回路连接一个平面，长宽分别为 \(x,y\) ，以x/2为轴，角频率 \(\omega\) 旋转平面，在 \(t=0\) 时刻，平面法向量与磁场夹角为0，那么旋转过程中，夹角为 \(\omega\)t 。如果初始时刻夹角为 \(\omega_0\) ,则旋转过程中夹角为 \(\omega_0+\omega t\) .这里讨论初始夹角为0的情况。

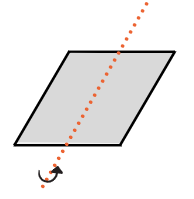
则此时磁通量为

\[\begin{align} \phi _B&=\underset{\text{open} \ \text{surface}}{\int } \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}}\\ &=x\ y\ B\ cos(\omega t) \end{align} \]

取导数可得

\[\begin{align} \frac{\text{d$\phi $}_B}{\text{dt}} &=-x\ y\ B\ \omega \ sin(\omega t)\\ &=\epsilon(t) \end{align} \]

可见，此时感生电动势随着时间变化。

因为感应电流等于感生电动势除以回路的电阻，所以感应电流也是随着时间变化的，即

\[I(t) =\frac{\epsilon (t)}{R} \]

式子中的 \(sin(\omega t)\) 告诉我们，当我们旋转这个回路的时候，电流将会以 正弦 的形式交替变化。

并且旋转的频率越快，感生电动势越大。

如果这个回路变为两匝，那么EMF也会变为2倍，因为两匝存在上下两个平面，磁场线穿过了两个平面，面积加倍，EMF变为两倍。EMF与匝数成正比。

面积、磁感应强度越大，旋转角频率越大，EMF越大，这就是交流发电机的基本思想。（虽然实际发电机角频率是一定的）

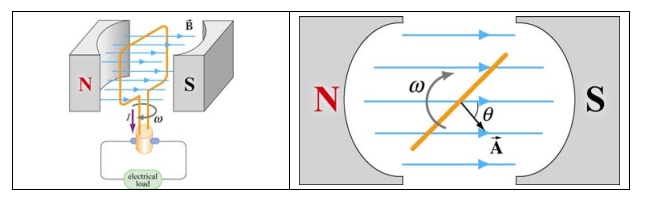
改变面积

还是一个矩形闭合导线回路，长为 \(x\)，不同的是一边用一个可以滑动的长为 \(l\) 导体棒代替，导体棒以速度 \(v\) 运动，所以 \(x\) 是变的。

假设磁场垂直纸面向外

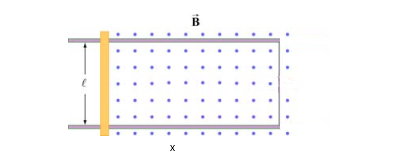
磁通量为

\[\begin{align} \phi _B&=\underset{\text{open} \ \text{surface}}{\int } \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}}\\ &=x\ l\ B\ cos(0)\\ &=x\ l\ B \end{align} \]

求导，位移导数就是速度，得

\[\begin{align} \frac{\text{d$\phi $}_B}{\text{dt}} &=-\frac{\text{dx}}{\text{dt}}\ l\ B\\ &=-v\ l\ B \end{align} \]

我们也可以通过做功导出EMF。

如果只看导体棒，在磁场中其所受到的洛伦兹力 \(F_l\) 与B、I垂直， 在这种情况下

\[F_l=I\ l\ B \]

如果将导体棒向右拉，磁通量减小，根据楞次定律，感应电流方向应该是自上往下，根据右手定则洛伦兹力 \(F_l\) 向左，我们施加的力要克服 \(F_l\) 做功，大小一样，而且是正功。我们做的功将会转变为EMF，产生感应电流作用在回路电阻上，以热量的形式散发掉。

功率 \(P_l\) 为（单位时间内做的功，所以x/t=v）

\[P_l=F_l\ v\ \]

功率又等于

\[P_l=\epsilon I \]

可得

\[\epsilon I =I\ l\ B\ v \]

故

\[|\epsilon| = l\ B\ v \]

我们只关心EMF的大小。因为楞次定律总可以告诉我们方向。

改变导体棒的运动方向，感应电流也随之反向，洛伦兹力也反向，所以我们总是做正功。

涡电流与磁制动

以下来自维基百科：https://en.wikipedia.org/wiki/Eddy_current

（机翻）一块金属板(C)在一个固定的磁铁下面向右移动。磁体北极N的磁场(B，绿色箭头)穿过薄片。由于金属在移动，通过薄片某一特定区域的磁通量也在变化。在薄片在磁铁前缘(左侧)下面移动的部分，通过薄片上某一点的磁场随着它越来越靠近磁铁而增加，\(\frac{dB}{dt}>0\) ,根据法拉第感应定律，这将在薄片上形成一个绕磁场线逆时针方向的圆形电场,这个电场产生了逆时针方向的电流，如图红色线。在薄片底部的磁铁尾缘(右侧)，磁场通过薄片上的一个给定点是减少的，因为它是远离磁铁的移动，\(\frac{dB}{dt}<0\) ,在薄片中顺时针方向诱导第二股涡流。

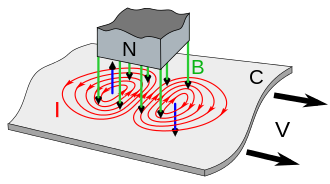
根据安培电路定律，薄片中的每一个圆电流都产生一个反向磁场(蓝色箭头)。根据楞次定律，通过薄片的反向场与磁场的变化相反。在磁铁的前缘(左边)，根据右手规则，逆时针方向的电流创造了一个指向上方的磁场，与磁铁的磁场相反，在薄片和磁铁的前缘之间产生排斥力。相反，在尾部边缘(右侧)，顺时针方向的电流引起一个指向下方的磁场，与磁铁的磁场方向相同，在薄片和磁铁尾部边缘之间产生一个吸引力。这两种力都阻碍了板块的运动。

在移动的过程中，会消耗动能，产生热量。她穿过磁场时，显然不会比没有磁场移动的更快。我们称为“磁制动”

消耗的热能越多，制动越快，减小涡流，就可以减小损耗。\(P=\epsilon I=I^{2}R\)