电磁学11.法拉第电磁感应定律

楞次定律

感应电流具有这样的方向，即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。

电流想要反抗磁场的改变，可以说是物理中最具人性的定律，因为我们都具有惯性，在一定程度上都拒绝改变。

如下图，只有在抽出和伸入的过程中（磁场变化），线圈才会产生感应电流，并且电流方向相反。静止时候（磁场恒定）电流为0。

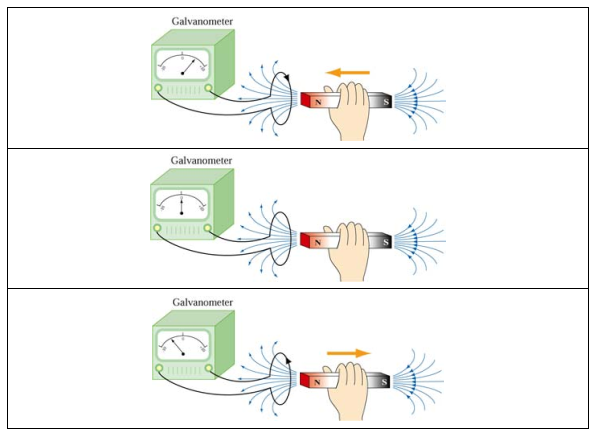
楞次定律在确定感应电流的方向时非常有用。

磁通量

与电通量类似。开曲面中，磁通量等于磁场与面积微元的点乘的积分：

\[\phi _B=\int \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}} =\int B \text{dA} \cos (\theta ) \]

dA的方向是微元面积的法向量的方向。

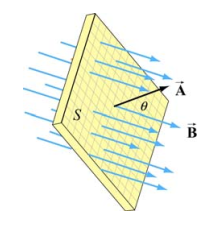
在闭合回路中，同安培环路定理中讨论一样，我们需要在回路上连接一个开曲面，代表讨论的只是穿过闭合回路内部的磁通量变化。

因为讨论通量，我们必须先定义我们的表面，通量只能通过表面。

法拉第电磁感应定律

法拉第大佬发现电磁感应现象：变化的磁场会产生电场。

法拉第大佬还发现，放在变化磁通量中的导体，会产生感应电动势。

他发现，这个电动势正比于感应回路中产生的磁场变化率，即

\[\epsilon \propto \frac{\text{dB}}{\text{dt}} \]

他还发现电动势正比于感应环路面积

\[\epsilon \propto A \]

因此猜测，电动势其实是这个感应环路面积内磁通量变化的结果。

将一条导线连接成环，使环内磁通变化，开曲面就是环内连接的纸面。这样我们就得到了一个闭合回路围绕的开曲面，假设导线长度为 \(l\) 。产生感应电流大小为 \(I\)。以下讨论均针对这种情况。

感应电动势的大小等于磁通量变化率的负值：

\[\epsilon =-\frac{\text{d$\phi $}_B}{\text{dt}} =-\frac{d}{\text{dt}} \underset{\text{open} \ \text{surface}}{\int } \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}} \]

为了体现楞次定律，感应电流反抗磁通的变化，加了个负号，使得数学上正确。

对于N匝线圈，总感应电动势将是其 \(N\) 倍

\[\epsilon =-N \frac{\text{d$\phi $}_B}{\text{dt}} \]

这是变压器的基本原理，通过匝数比得到我们想要的电压。

回忆前面内容，电源电动势在数值上等于非静电力在电源内部把正电荷从电源负极移动到电源正极所做的功。

类比，这里的“非静电力”，就是“磁通的变化率”。

如果站在这个导体（导线/线圈）里面，沿着电流的方向前进，显然导线中每个地方都应该能看到电场，沿导线一周，则感应电动势等于

\[\epsilon=\underset{\text{close}\ \text{loop}}{\oint }\overset{\rightharpoonup }{E} \overset{\rightharpoonup }{\text{dl}} \]

个人理解：类比前面的电源电动势，在电源中电动势就是内部非静电力做的功，在不计内阻的情况下，她应该等于外部负载上的电势差，而电势差是外部单位电荷在静电力下所做的功，单位电荷做的功就是Edl的环路积分。

综上:

\[\epsilon=\underset{\text{close}\ \text{loop}}{\oint }\overset{\rightharpoonup }{E} \overset{\rightharpoonup }{\text{dl}} =-\frac{d}{\text{dt}} \underset{\text{open} \ \text{surface}}{\int } \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}} \]

其中

close loop代表闭合回路。

open surface 表示开曲面，必须连接到回路上。

这就是法拉第电磁感应定律。

关于KVL

有趣的是，基尔霍夫电压（KVL）定律告诉我们，绕回路一圈，Edl的闭合回路积分总是0（这是KVL的本质，单位电荷绕一圈做功为0），但是在有变化磁通的时候，KVL是不成立的。变化的磁通会让导线内部的电场变成非保守的，基尔霍夫定律只有在电场是保守场的情况下才成立。保守场做功与路径无关，两点之间的电势差唯一确定；而非保守场则与路径有关，这个实验中，绕一圈将得到一个电动势。所以我们现在处理的是非保守场，基尔霍夫定律只是法拉第定律的特例（磁通变化率为0的时候）。法拉第定律总是有效的。
这是Walter Lewin教授在课程上讲的内容。

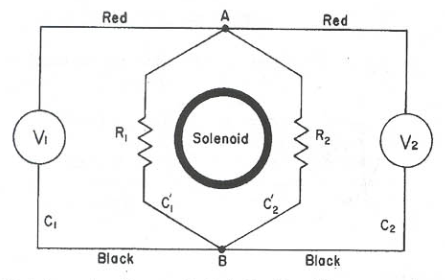
如图，R1≠R2，当中间通电螺线管的磁通变化时，且磁场影响整个电路时，V1≠V2.

这个结论引发Walter Lewin和ElectroBOOM整流侠对这个结论的争议，整流侠最后对争议做了总结，链接：

https://www.bilibili.com/video/av39313806

现在《电路分析》中，《电路（第五版）》（邱关源）中对KVL的定义是“在集总电路中，任何时刻，沿任一回路所有支路电压的代数和恒等于零”（P31）。分析的是集总参数电路，指分析电感和电容之类的元件时，要把她们当成集总电路元件，把元件的场固定在那个元件之内，不泄露到外面出去，这样我们就可以方便地计算各个元件两侧的电压，这使得KVL在各个场合下都可以使用。

此时，元件内部和外部的物理性质就可以单独分析。

而Walter Lewin做的实验，就是非集总电路，通电螺线管产生的变化磁场影响到周围的元件和导线。使得电路分析变得复杂。
解决方式就是等效成集总电路，把等效电阻/等效电感/等效电容单独拿出来分析。