电磁学10.安培环路定律

安培环路定律

由毕奥法萨尔定律我们知道，在无限长载流导线中，在半径为 \(r\) 的区域磁感应强度为

\[B=\frac{ \mu _0 I}{2 \pi r} \]

如果把该圆无限分割成小的微元 \(dl\) （与前面导线长度微元dl区分）。计算 \(B d\)l 沿着该闭合圆周的积分，可得

\[\oint\overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}=B 2 \pi r \]

而

\[B 2 \pi r= \mu _0 I \]

故

\[\oint\overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}=\mu _0 I \]

这个式子告诉我们，不管绕多远，\(Bdl\) 的积分都等于 \(\mu _0 I\)

因为 B 与 r 半径成反比。

注意，\(B\) 与 \(dl\) 是点乘。

安培大佬发现，不一定非要沿着圆周运动才能得到 \(\mu _0 I\) 。可以沿着任意弯曲的闭合路径积分。

结果仍然可以得到

\[\oint\overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}=\mu _0 I \]

定义：

在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率。这个结论称为安培环路定理（Ampere circuital theorem）

这个定义中，被“包围”的定义有些不太完善，下面进行补充。

任意选择一条闭合路径，我们需要给这条闭合路径加一个开曲面，任何开曲面都可以，但是必须连接到该闭合路径上（就像一个袋子）。

只有穿过这个开曲面的电流，我们才真正地说她是“被包围”，可以说，就是穿过闭合路径和开曲面的电流。

从开口环路看进去，如果按环路顺时针CW转动为正方向，根据右手定则，

1. 如果电流产生的磁场是顺时针的，则规定 \(I>0\) .
2. 如果电流产生的磁场是逆时针的，则规定 \(I<0\) .

如果按环路逆时针CCW转动为正方向，

1. 如果电流产生的磁场是逆时针的，则规定 \(I>0\) .
2. 如果电流产生的磁场是顺时针的，则规定 \(I<0\) .

但我们应用的时候，都会选择简单的路径去简化计算。

通电导线的磁场

导线半径为 \(R\) ，假设电流均匀地分布在导线上，电流密度均匀，计算导线任意的磁场。

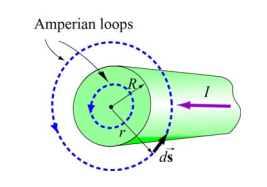
选择一个半径为 \(r\) 的圆形路径，因为圆的对称性，能保证路径上每处磁场相等。选择一个开曲面连接到环路上。因为电流是朝向纸面向外，所以根据右手定则，选择环路逆时针转动方向为正方形，这样电流也是正的。

当 \(r>R\) 时

根据安培环路定理可得

\[B 2\pi r = \mu _0 I\rightarrow B= \frac{ \mu _0 I}{2 \pi r} \]

此时磁感应强度大小随环路半径 \(\frac{1}{r}\) 下降。

当 \(r<R\) 时

因为此时不是全部电流都在环路里面，所以需要注意是多少电流，因为前面假设在导线中电流密度一样，所以环路内的电流其实就是横截面积之比 \(\frac{2 \pi r^2}{2 \pi R^2}\) 乘以总电流 \(I\)。

\[B 2\pi r = \mu _0 \frac{r^2}{R^2}I\rightarrow B= \frac{ \mu _0 I r}{2 \pi R^{2}} \]

此时磁感应强度大小随环路半径 \(r\) 线性增加。哇，好神奇是不是。

当 \(r=R\) 时

上面两个式子的结果都是一样的，此时r变成R：

\[B= \frac{ \mu _0 I}{2 \pi R} \]

如果横轴是r，纵轴是磁感应强度B，可以画出来：

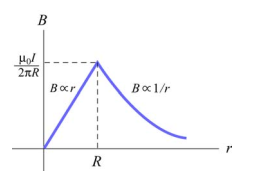
导线表面上磁感应强度是最大的。

通电螺线管的磁场

先感性认识一下，看下图有一个电流环（理解随便找的），点圆表示朝纸面向外，磁场呈逆时针，叉圆表示朝纸面向里，磁场呈顺时针。两者中间就会有很少数磁场线是直线，多数磁场线是朝两边弯曲发散的。

但如果在旁边有相同的电流环，下面左图，右边的这些电流环会使发散的磁场线收缩起来，内部就会形成近乎恒定的磁场，

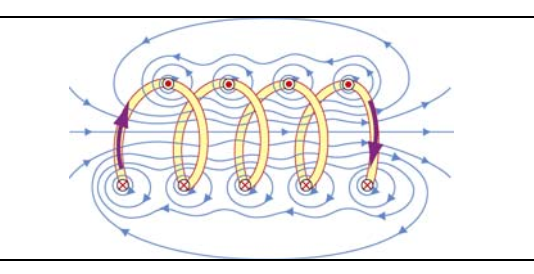
电流环缠绕越紧，在内部，磁场的恒定程度越大，如下面右图。而外部的磁感应强度是很小的。

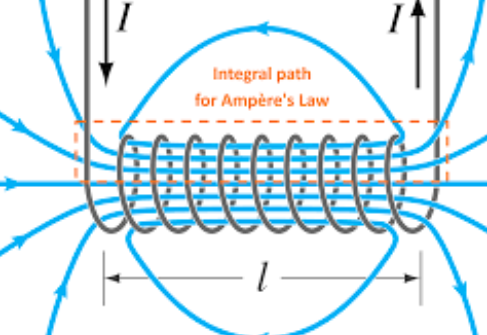
那么，螺线管内部磁感应强度是多大呢？

假设螺线管长度为大写 \(L\) ，螺线管有 \(N\) 匝，内部磁场恒定。从左边看进去，电流顺时针流动，根据右手定则我们知道磁场自左向右，假设螺线管外部的磁场为0。

应用安培环路定理我们首先需要选择一条闭合路径——一条长边为 \(l\) 在螺线管中间的矩形。

按矩形的四条边分为4个部分。

\[\begin{align} \oint \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}&=\int_1 \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}} + \int_2 \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}+ \int_3 \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}} +\int_4 \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dl}}\\ &=0+0+Bl+0\\ &=Bl \end{align} \]

因为

对第一条边，我们假设螺线管外部磁场为0，所以积分为0

对第二、四条边，在螺线管外面的部分磁场为0，这部分积分为0，在螺线管内部，因为 \(dl\) 与磁场方向垂直，所以点乘结果为0。

故只有第三条边有贡献。

用矩形边内的纸面作为我们的曲面，穿过曲面的电流是多少，需要知道线圈穿过这个曲面多少次，用比例关系可以求出，\(L\) 上有 \(N\) 匝，所以 \(l\) 上匝数为

\[n=\frac{l N}{L} \]

所以穿过曲面总的电流就是

\[\frac{l N}{L} I \]

故

\[Bl=\mu _0 \frac{l N}{L} I \]

可得

\[B=\mu _0 \frac{ N}{L} I \]

在螺线管的长度远大于半径时，这是对螺线管内部磁场一个很好的近似。

磁感应强度正比于单位长度的匝数。因为第一匝线圈产生的磁场类似磁偶极子，在远处，磁场削减的很快，可能几乎感受不到，所以即使多匝，但每匝距离较远，在另一端磁感应强度也不会明显增强。而增大单位长度的匝数，实际上是把每个匝数的磁场叠加，多匝进行压缩在一起，磁场叠加。