电磁学9.毕奥-萨法尔定律与高斯磁定理

通电直导线的磁场方向我们可以通过右手定则判断出来。也可以在导线周围放置磁铁判断出来方向，她们会排成一个圆圈，假设这个圆圈的半径是 \(R\) 。

通过实验可知，磁感应强度大小和电流成正比，和半径成反比。这也符合直观上认识。

怎么计算通电直导线周围空间中某点磁感应强度呢？

毕奥萨法尔定律

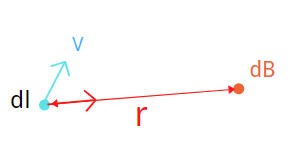
如果有小电流元 \(dl\) ,在距离为 \(r\) 的一点产生的磁场是多少？

假设两点之间的方向单位矢量为 \(\hat{r}\) 。

根据右手定则判断通电直导线的磁场方向，可以知道B垂直纸面向里。

每个小单元 \(dl\) 在 \(r\) 点贡献的磁场的大小可以用毕奥-萨法尔定律得出：

\[\text{dB}=\frac{ C I \left( \overset{\rightharpoonup }{\text{dl}} * \hat{r}\right)}{r^2} \]

其中 \(C\) 是常数。国际单位中 \(C=10^{-7}\) 。也可以写成

\[C=\frac{\mu _0}{4 \pi } \]

\(\mu _0\) 为真空磁导率。

\(dB\) 与电流大小成正比，与导线长度 \(dl\) 成正比，与距离的平方成反比。为了得到正好垂直于纸面的方向，我们需要叉乘单位矢量 \(\hat r\) .

对每段 \(dl\) 积分，我们就能得出整段导线在 \(r\) 点产生的磁感应强度。

载流直导线周围的磁场

如果磁单极存在的化，磁单极周围的磁感应强度就会按 \(\frac{1}{r^2}\) 规律下降，以前在点电荷的静电场中，电场也是按 \(\frac{1}{r^2}\) 规律下降，重力场也是。（啊感觉物理又统一了有没有）。可惜的是没有目前没有发现磁单极。

在通电直导线中，假设导线上任意一点距离某点距离为 \(r\) ,该点与导线垂直距离为 \(R\) 。

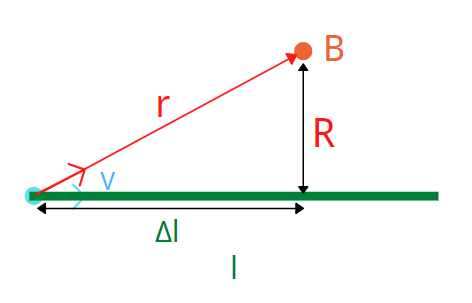
利用毕奥萨法尔定律，可得每段微小单元dl在r点产生磁场的大小，然后对整段长度积分，可得

\[B=\int \frac{ \mu _0 I \sin (\theta )}{4 \pi r^2} \, dl \]

其中，我们根据三角函数关系，又可以得到

\[Δl=R \cot (\theta ) \]

\[R=r \sin (\theta ) \]

代入可得

\[\begin{align} B&=\int \frac{ \mu _0 I \sin (\theta )}{4 \pi r^2} \, dl\\ &=\frac{ \mu _0 I}{4 \pi } \int_{}^{} \frac{\sin (\theta )}{r^2} \, d(R \cot (\theta ))\\ &=\frac{ \mu _0 I}{4 \pi } \int_{\theta _1}^{\theta _2} -\frac{R \sin (\theta )}{r^2 \sin^{2} (\theta )} \, d\theta\\ &=\frac{ \mu _0 I}{4 \pi } \int_{\theta _1}^{\theta _2} -\frac{1 }{r} \, d\theta\\ &=\frac{ \mu _0 I}{4 \pi R} \int_{\theta _1}^{\theta _2} -\sin (\theta ) \, d\theta\\ &=\frac{ \mu _0 I}{4 \pi R} (cos(\theta_1)-cos(\theta_2))\\ \end{align} \]

若导线为无穷长（R《 l ），则 \(\theta_1 =0，\theta_2 = \pi\)

所以

\[\begin{align} B&=\frac{ \mu _0 I}{4 \pi R} (cos(\theta_1)-cos(\theta_2))\\ &=\frac{ \mu _0 I}{4 \pi R} (1-(-1))\\ &=\frac{ \mu _0 I}{2 \pi R}\\ \end{align} \]

无限长载流导线周围的磁感应强度的大小与场点到导线的距离成反比。按 \(\frac{1}{R}\) 比例下降。

电流环中心的磁场

也可以通过毕奥萨法尔定律计算圆型载流导线中心的磁场。

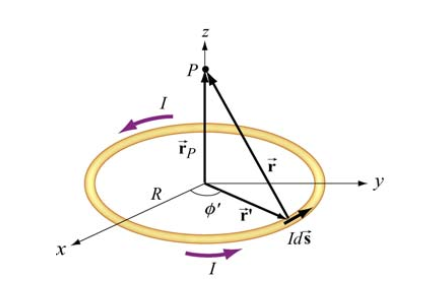
用右手定则我们可以知道中心磁场方向是向上的。

根据毕奥萨法尔定律，可得电流环中心总的磁场为：

\[B=\int \frac{ \mu _0 I \sin (\theta )}{4 \pi R^2} \, dl \]

由于圆的性质，单位矢量 \(\hat r\) 与 $ dl$ 总是垂直的，所以夹角的正弦就是1。圆的周长我们很轻松地可以计算出来 $2 \pi R $

所以

\[B=\frac{ \mu _0 I}{4 \pi R^{2}} *2 \pi R =\frac{ \mu _0 I}{2 R } \]

高斯磁定律

如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。这个规律类似于电场中的高斯定理，因此也称为高斯定理。
也就是说，对任意闭合面对 \(BdA\) 做积分求磁通量，结果总是0.

\[\oint \overset{\rightharpoonup }{B} \overset{\rightharpoonup }{\text{dA}}=0 \]

因为静电场是有源场，它的电场线不会闭合，所以对一个封闭曲面的通量不一定为0；而稳恒磁场是无源场，它的磁场线是封闭的，有多少条磁场线穿出曲面，相应就有多少条磁场线穿进曲面，所以磁场对一个封闭曲面的通量恒为0。用比较专业的场论术语来说，就是：静电场是有源场，散度一般不为0；稳恒磁场是无源场，散度恒为0
高斯磁定定理，告诉我们磁单极子不存在。磁的基本实体是磁偶极子，而不是磁荷。（找到磁单极，可能这条结论就会被改写）。

这时麦克斯韦方程组的第二个方程。