电磁学7.磁场与洛伦兹力

磁场

磁场和电场类似，磁场是一种看不见、摸不着的特殊物质，磁场不是由原子或分子组成的，但磁场是客观存在的。磁场具有波粒的辐射特性。磁体周围存在磁场，磁体间的相互作用就是以磁场作为媒介的，所以两磁体不用接触就能发生作用。电流、运动电荷、磁体或变化电场周围空间存在的一种特殊形态的物质。由于磁体的磁性来源于电流，电流是电荷的运动，因而概括地说，磁场是由运动电荷或电场的变化而产生的。

磁极

条形磁铁由两个极组成，分别为北(N)和南(S)。磁场在两极最强。磁力线从北极出发，进入南极。

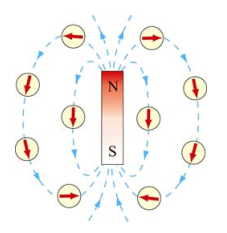
磁极同样存在同性相斥，异性相吸现象。

电和磁有一个很大的不同。电有两个极，两极可以单独出现（单独的正极/负极）；但是磁极总是成对出现，单独的极是不存在的。

安培定则

安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。

通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向直导线中电流方向，那么四指指向就是通电导线周围磁场的方向；

通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，让四指指向电流的方向，那么大拇指所指的那一端是通电螺线管的N极。

磁感应强度

我们定义电场强度是通过静电力，电场强度是单位电荷所受到的静电力。

磁力是不是磁荷乘以磁场强度？

不是，因为我们暂时还没有发现磁单极。如果有磁单极，就没问题。

取一个电荷量为 \(q\) 的电荷，电荷运动速度是 \(v\) ，周围存在磁场。

实验显示，电荷受到的力总是垂直于它速度的方向。即

\[\overset{\rightharpoonup }{F_B}\bot \overset{\rightharpoonup }{v} \]

因为磁场力永远垂直于速度方向，所以磁场力永远不会对电荷做功。

这个力的大小正比于电荷的速度，同时正比于电荷本身的大小。

定义：

\[\overset{\rightharpoonup }{F_B} = q（\overset{\rightharpoonup }{v}\Lambda \overset{\rightharpoonup }{B}）\\ \left| F\right| =q v B \sin(\theta) \]

其中，B是磁感应强度，v是电荷速度，两者叉乘。

注意是叉乘。因为叉积的几何意义在三维中，就是两个向量叉积后，得到的向量与这两个向量垂直。有洛伦兹力，她和电荷有效运动（速度）方向，磁感应强度方向三者一定是一个垂直关系。

磁场强度 \(B\) 在国际单位中，单位是特斯拉（T）。

1T是非常强的磁场，因此我们经常用高斯（G）作为单位，高斯与特斯拉换算为

\[1G=10^{-4}T \]

地球的磁场大概是半高斯。

洛伦兹力

运动电荷在磁场中所受到的力称为洛伦兹力。单位是牛顿。

彩色电视内部的电子枪会对屏幕进行光栅扫描，电子束的强弱变换产生出图像，如果在电视周围放一个很强的磁铁，她就会扭曲图像，因为她影响到电子的运动。如果显像管被严重磁化后就造成永久性损伤。（懂了懂了明天就给老友送一个……）

如果电荷周围有电场也有磁场的话，例如当电荷在载流导线附近移动时，合力 \(F_s\)是电场力和磁场力的矢量和：

\[\overset{\rightharpoonup }{F_s} = q（\overset{\rightharpoonup }{E}+\overset{\rightharpoonup }{v}\Lambda \overset{\rightharpoonup }{B}） \]

根据洛伦兹力的定义，这个合力也可以说是洛伦兹力。

通电导线上电流为 \(I\) 。磁场在导线各个位置上完全可能是不同的。

电流上一个电荷 \(+dq\) ，正以漂移速度 \(V_d\) 通过导线。

思考一下，电流是0的时候，因为此时电荷属于热运动，是随机运动，电荷上合力为0。当电流不等于0时，电荷移动，合力不为0.

为什么要用正电荷？电流不是电子移动产生的吗？是的，只是出于数学上的考虑，负电荷乘以矢径，等价于正电荷乘以相反方向的矢径。只是根据电流方向的定义考虑，用正电荷描述方便。

假设 \(V_d\) 与 \(B\) 夹角为 \(\theta\) ,磁场力为

\[d\overset{\rightharpoonup }{F_B} = dq（\overset{\rightharpoonup }{v_d}\Lambda \overset{\rightharpoonup }{B}） \]

因为电流是单位时间内流过的电荷量：

\[I=\frac{\text{dq}}{\text{dt}} \]

故

\[d\overset{\rightharpoonup }{F_B} = I dt（\overset{\rightharpoonup }{v_d}\Lambda \overset{\rightharpoonup }{B}） \]

又根据经典力学，速度乘以时间等于距离：

\[dl=dv*dt \]

\(dl\) 是沿导线的一段距离。

故

\[d\overset{\rightharpoonup }{F_B} = I （\overset{\rightharpoonup }{dl}\Lambda \overset{\rightharpoonup }{B}） \]

从这个式子可知，\(d\overset{\rightharpoonup }{F_B}\) 是这一段 \(\overset{\rightharpoonup }{dl}\) 上所受到的力，\(\overset{\rightharpoonup }{B}\) 是 \(dl\) 局部的磁感应强度。

如果想知道整个导线上受到的力，必须沿整个导线积分，并且要确定每一小段 \(dl\) 上的 \(\overset{\rightharpoonup }{B}\) 。这样每一小段都得到一个力，再叠加。有点繁琐，但这是基本思想。

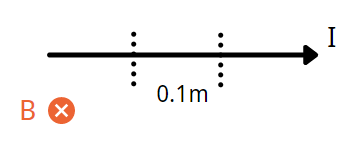
简化计算，只能简化模型，假如一条通电直导线，电流为 \(300A\) ，在 \(l=0.1m\) 范围内，磁场保持 \(0.2T\) 恒定，垂直纸面向里。

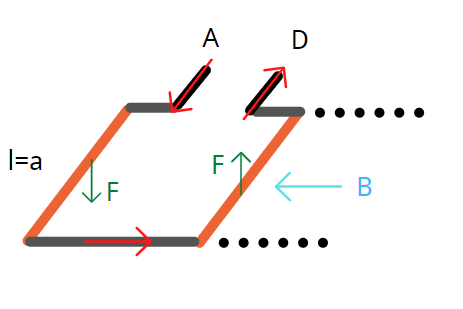
因为速度与磁场夹角是90度，很容易得到这段长度上的洛伦兹力大小：

\[F_B =I*l*B=300*0.1*0.2=6N \]

通电线圈（电动机）

假设一个通电线圈，红色箭头表示电流流向，虚线区域内有从右到左的一个恒定均匀的磁感应强度为 \(\overset{\rightharpoonup }{B}\) 的磁场。通电线圈的左右两臂（黄色表示）会受到磁场力 \(\overset{\rightharpoonup }{F}\)，灰色区域由于电流流向与磁场方向平行，所以叉积为0，不会受到磁场力。通过左手定则，可以判断力的方向。

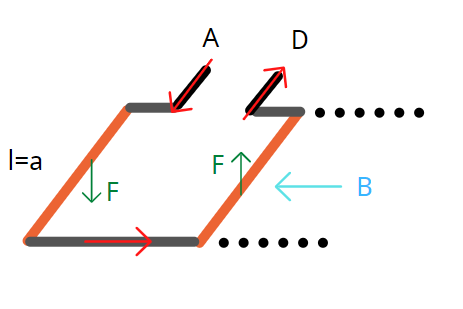
如果左右两臂的长度为 \(a\) 。则

\[F=I*a*B \]

两个臂的力大小相等，方向相反，使得线圈逆时针旋转。

某个时刻，旋转90°后，力矩变为0。但是由于惯性，会继续旋转，逆时针旋转超过90°后，力矩就会反过来。其实通过D、A位置就能看出，旋转180°后，D在左边，A在右边。然后翻转过来，来回摆动。显然这不能算是电动机。

所以需要一个滑动的机械结构-电刷和换向器。

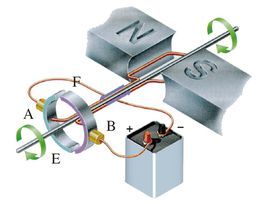
电刷是与运动件作滑动接触而形成电连接的一种导电部件。电刷是用于换向器或滑环上，作为导入导出电流的滑动接触体。

结构上，换向器是几个接触片围成圆型，分别连接转子上的每个触头，外边连接的两个电极称为电刷与之接触，同时只接触其中的两个。

通过电刷和换向器，每一次旋转，电流就会自动的改变方向，解决了力矩反转的问题，并且解决了旋转过程中导线缠绕的问题。