电磁学1.高斯定律

库伦定律

库仑定律（Coulomb's law）是静止点电荷相互作用力的规律。

真空中两个静止的点电荷之间作用力与她们电荷量乘积成正比，与距离的平方成反比，可以表示为

\[\overset{\rightharpoonup }{F}=k\frac{q_1 *q_2* \overset{\rightharpoonup }{e}}{r^2} \]

\(k\) 为库伦常量，\(\overset{\rightharpoonup }{e}\) 表示方向矢量。

有时候 \(k\) 也会写成：

\[k=\frac{1}{4 \pi \epsilon _0} \]

\(\epsilon _0\) 是真空介电常数。

电场

电场是电荷及变化磁场周围空间里存在的一种特殊物质。这种物质与通常的实物不同，它虽然不是由分子原子所组成的，但它却是客观存在的特殊物质，具有通常物质所具有的力和能量等客观属性。

生场电荷 \(Q\) 产生的电场 \(\overset{\rightharpoonup }{E}\) 可以通过检验电荷 \(q\) 求出：

\[\overset{\rightharpoonup }{E}=\frac{\overset{\rightharpoonup }{F}}{q} \]

检验电荷上作用力通过库伦定律求出，代入可得：

\[\overset{\rightharpoonup }{E}=k\frac{Q* \overset{\rightharpoonup }{e}}{r^2} \]

作用力取决于小 \(q\) ,但是电场不是，电场只表征大 \(Q\) 周围的产生的情况，从式子中可以理解为单位电荷所受到的电场力。所以电场的意义在于，在某一位置引入电荷，我们都能知道她所受到的力的大小和方向。

电通量

开放曲面

通过微元面积 \(dA\) 电通量定义为：电场向量 \(E\) 乘以该微元面积上法向量 \(\hat{n}\) 再乘以微元面积 \(dA\)
直观上理解就是穿透给定表面的电场线的数目称为“电通量”。因此，电场可以看作是单位面积上的电场线数。

\[\text{d$\phi $}= \overset{\rightharpoonup }{E}*\hat{n}*\text{dA} \]

一般教材上把 \(\hat{n}*\text{dA}\) 简化为向量 \(\overset{\rightharpoonup }{\text{dA}}\)，此时 \(\overset{\rightharpoonup }{\text{dA}}\) 永远垂直于面单元 \(dA\)，再通过点乘公式算出，即

\[\text{d$\phi $}= \overset{\rightharpoonup }{E}*\overset{\rightharpoonup }{\text{dA}}=E*dA*cos\theta \]

我的直观理解是垂直穿过该面积的电场线多少，因为是垂直，所以运用向量内积计算，内积几何含义就是一个向量在另一个向量上的投影的积，就是同方向的积。

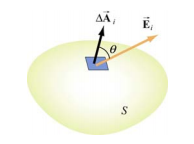
整个开放曲面上通过电通量可以通过积分写出

\[\phi=\int\overset{\rightharpoonup }{E} *\overset{\rightharpoonup }{\text{dA}} \]

类比

类比气/液体体积流量计算：

体积流量（Volume Flowrate）是单位时间里通过过流断面的流体体积。

设水管是圆柱形的，则流速(v) 乘以时间(t) 就是该时间内圆柱内总液体的长度 L=vt，其实流速=每秒经过柱体的高。

再乘以横截面积(s) 就是总体积 V=Ls ——圆柱的体积公式：底面积乘高。
那么单位时间的体积，就是总体积除以时间。

\[VF(流量)=V/t=Ls/t=vts/t=vs \]

闭合曲面

如果是闭合曲面，则

\[\phi=\oint \overset{\rightharpoonup }{E} *\overset{\rightharpoonup }{\text{dA}} \]

结果是标量，如果等于零，可以理解为进去多少空气，就出来多少空气。

点电荷上电通量

电场向量和微元面积的法向量都径直向外，所以夹角为0.

每处的电场大小相等。

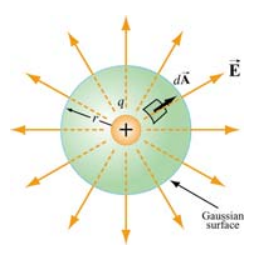
计算点电荷表面上的电通量大小很简单：

\[\phi= 4 \pi r^2 E \]

电场我们可以计算出来：

\[{E}=\frac{Q* \overset{\rightharpoonup }{e}}{4 \pi \epsilon _0r^2} \]

代入可得：

\[\phi=\frac{Q }{ \epsilon _0} \]

可见，与距离无关。不难理解，就像空气向外流，不论球有多大，出去的量是一定的。

通量由中心的电荷量决定。

所以，如果不是球体，而是任意形状的闭合曲面，她的气流量还是一样。同样能得到这个结果。

高斯定律

在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷量的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。即：

\[\phi=\oint \overset{\rightharpoonup }{E} *\overset{\rightharpoonup }{\text{dA}}=\frac{\sum _{ } Q}{\epsilon _0} \]

不管封闭曲面形状如何选取，都成立。

这是麦克斯韦方程组四个方程的第一个。

高斯定律和库伦定律某种意义上是同一种定律，都构建了电场与电荷的关系。