线性代数15.投影到子空间

一维投影

我们将从 \(b\) 投影到 \(a\) 说起，\(a\) 上离 \(b\) 点最近的点是 \(p\) ,\(bp\) 垂直于 \(a\) ,距离 \(e=b-p\) (向量减法)，\(p\) 就是投影点。

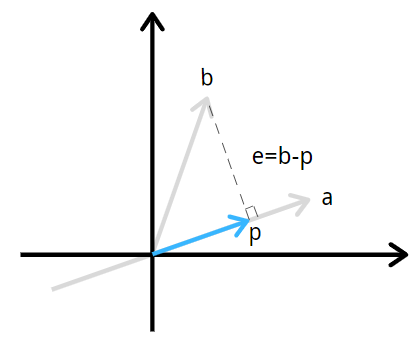
向量 \(p\) 就是 \(b\) 在 \(a\) 的投影。关键就是垂直。

\(p\) 是 \(a\) 的某个倍数。我们可以记为 \(p=xa\) .

\(x\) 就是我们要找的。

投影矩阵P

因为 \(a\) 与 \(e\) 垂直，可得

\[a^T(b-xa)=0 \]

展开得

\[xa^Ta=a^Tb \]

从矩阵乘法可以知道（一行点乘一列）， \(a^Ta\) 是一个数字，所以我们可以两边同时除以 \(a^Ta\)

\[x=a^Tb/a^Ta \]

所以 \(p\) 可以表示为

\[p=a\frac{ a^{\text{T}}b}{a^{\text{T}}a} \]

先消化一下这个式子

若 \(b\) 翻了一倍变成 \(2b\) ,投影 \(p\) 也变成 \(2\) 倍。

若 \(a\) 变成 \(2a\) ,投影 \(p\) 不变。从几何看，就是 \(p\) 还是那个位置；从 \(p\) 式子上看，分母和分子会乘以相同倍数，抵消掉了。

让我们从矩阵角度思考这个式子，投影 \(p\) 是一个投影矩阵作用于某个向量。我们将投影矩阵记为 \(P\) ,该例子作用于 \(b\) :

\[p=Pb \]

而且可知

\[P=\frac{a a^{\text{T}}}{a^{\text{T}}a} \]

她不等于 \(1\) ,因为分母是行乘列，结果一个数字，而分子是列乘行，结果是一个矩阵。

如果 \(a\) 是 $ n$ 维，那么 \(a.a^T\) 是 \(n*n\) 矩阵。

\(P\) 将 \(b\) 投影于 \(a\) ,是这个矩阵生成了投影。

\(P\) 的性质

1. 列空间定义告诉我们，无论把矩阵乘以什么，最终都会停留在该列空间，所以\(P\) 乘以任何向量 \(b\) ,最终都会停留在 \(P\) 的列空间 \(C(A)\).

   \(C(A)\) 是通过 \(a\) 的一条直线。

   \(P\) 的秩是 \(1\).

2. \(P\) 是对称矩阵，有 \(P^T=P\)

3. 将 \(b\) 投影两次，第二次投影的结果和第一次一样，投影还是在相同的位置，有 \(P^2=P\)

投影的意义

上一解我们就讨论过，\(Ax=b\) 也许无解。而我们希望利用上所有的数据，问题就在于怎么微调 \(b\) .

我们可以将 \(b\) 变为列空间中最接近她的那一个，把无解变成有解，将\(Ax=b\) 变为

\[A\hat x=p \]

其中，\(p\) 是 \(b\) 在列空间上的投影。

\(\hat x\) 不同于 \(x\) ,因为 \(x\) 是不存在的，\(\hat x\) 表示的是最接近结果的解。

解决 \(Ax=b\) 无解问题，我们首先需要找到列空间中最接近 \(b\) 的是什么，这就是投影的意义。

一维中，我们将 \(b\) 投影到 \(a\) ,求得 \(a\) 空间中距离 \(b\) 最近的向量 \(p\).

二维投影

我们将其与方程 \(Ax=b\) 联系起来。平面是 \(A\) 的列空间\(C(A)\),

\[A=\left( \begin{array}{cc} a_1 & a_2 \\ \end{array} \right) \]

\(a_1、a_2\)线性无关构成 \(C(A)\) 的一组基。

若 \(b\) 在 \(C(A)\) 里面，投影结果就是 \(b\) 自己。但显然，上图向量 \(b\) 不在 \(C(A)\) 里面。我们希望找到将 \(b\) 投影到平面上最近点的漂亮公式。

通常有一个误差向量 \(e=b-p\) ，一般不为零。当 \(e\) 垂直于平面时长度最小。

\(p\) 在 \(C(A)\) 中，所以 \(p\) 可以由平面的基向量表示为

\[\begin{align}\\ p & =\hat x_1a_1+\hat x_2a_2\\ & =A\hat x \end{align} \]

所以我们的问题到这里就转换为，寻找合适的 \(A\) 的列组合，让 \(e=b-p=b-A\hat x\) 垂直于平面。

由于 \(e\) 垂直于平面， 所以\(e\) 垂直于平面里面任意向量，可得

\[a_1^T(b-A\hat x)=0\\ a_2^T(b-A\hat x)=0\\ \]

可以将其表示为矩阵形式：

\[\left( \begin{array}{c} a^T{}_1 \\ a^T{}_2 \\ \end{array} \right).(b-A \hat x)=\left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right) \]

等价于

\[A^T(b-A\hat x)=0 \]

\(e\) 位于 左零空间 \(N(A^T)\) .由上节课可知，左零空间和列空间是正交关系，所以 \(e\) 垂直于 \(A\) 的列空间。

\[e \quad \bot \quad C(A) \]

现在开始解方程 \(A^T(b-A\hat x)=0\)

展开：

\[A^TA\hat x=A^Tb \]

两边同时乘以 \((A^TA)^{-1}\),

\[\hat x=(A^TA)^{-1} .A^Tb \]

这就是方程的解。

投影 \(p\) 的公式为：

\[p=A\hat x=A(A^TA)^{-1} .A^Tb \]

投影矩阵 \(P\) :

\[P=A(A^TA)^{-1} .A^T \]

\(\hat x、p、P\) 这三个公式适用于 \(n\) 维情况。

需要注意的是，如果矩阵 \(A\) 不是方阵，那么 \(A^{-1}\) 是不存在的，所以我们不能把 \((A^TA)^{-1}\) 展开，只能保留。

投影矩阵 \(P\) 性质

和一维一样，同样存在

1. \(P^T=P\)

2. \(P^2=P\)

证明过程改变乘法顺序，就能得到单位阵消掉，不再累述。

应用

最常见的例子是通过最小二乘法拟合一条直线。

比如，我们现在有3个点，\((1,1)、(2,2)、(3,2)\)，横坐标表示时间 \(t\) ,纵坐标bi表示数据 \(b\) .我们希望求出 "最优的直线"，误差越小越好。

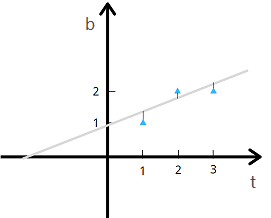
设最优直线为 \(b=C+Dt\) ,我们的目标就是求出 \(C、D\)。

根据三个点我们可以得到三个方程：

\[C+D=1\\ C+2D=2\\ C+3D=2 \]

从而可以得到 \(Ax=b\) 的矩阵形式：

\[\left( \begin{array}{cc} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \end{array} \right).\left( \begin{array}{c} C \\ D \\ \end{array} \right)=\left( \begin{array}{c} 1 \\ 2 \\ 2 \\ \end{array} \right) \]

注意这个方程无解。但我们可以求出最优解。

我们将两边同时乘以\(A^T\),通过投影获得一个有解的方程。

下节课继续。