线性代数11.矩阵空间、秩1矩阵和小世界图

矩阵空间

矩阵空间就是一些矩阵的集合。

向量空间的运算同样适用于矩阵空间，可以进行矩阵加法和数乘，注意不包括矩阵相乘，矩阵空间只考虑加法和数乘封闭性。

把 \(R^n\) 的概念延申到 \(R^{n*n}\),矩阵空间可以看成一种新的向量空间。

\(3*3\) 矩阵

以下讨论均以 \(3*3\) 矩阵 为例：

3*3矩阵构成矩阵空间记为 \(M\) ,子空间有

1. 上三角矩阵,记为 \(U\)
2. 对称矩阵,记为 \(S\)
3. 对角矩阵，记为 \(D\)

我们想要知道她们的维数，就需要看她们的基由多少个向量组成。

M

类比向量，一个向量有n个可以独立变化的元素，就在n维空间里面，类似的，所有3*3矩阵有9个可以独立变化的元素，所以她在9维空间里面。

M的基由9个矩阵构成：

\[\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\,,\left( \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\,,\left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\text{...}\left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \]

S

对称矩阵有6个可以独立变化的元素，所以她在6维空间里。

U

上三角矩阵有6个可以独立变化的元素，所以她在6维空间里。

D（S∩U）

S∩U就是对角矩阵，对角矩阵有3个可以独立变化的元素，所以她在3维空间里。

S+U

S+U的意思是，任取S和U中元素/矩阵相加构成新矩阵，最终可以得到所有3*3矩阵，在9维空间里面。

定理

从上面分析中，我们可以得到：

\[dim（S）+dim（U）=dim（S∩U）+dim（S+U） \]

这个式子是通用的。

拓展

我们构造一个新的没有向量的向量空间。她来自微分方程。

\[\frac{d^2y}{dx^2}+y=0 \]

解是 \(y=C_1cosx+C_2sinx\).

这是一个向量空间，一组基就是 \(cosx\) 和 \(sinx\) ,维度是2，

这个例子的要点是，这些不是向量，是函数，但我们可以当成向量来看待。

所以线性代数内容不仅仅可以用于矩阵。

秩为1矩阵

\[A=\left( \begin{array}{ccc} 1 & 4 & 5 \\ 2 & 8 & 10 \\ \end{array} \right) \]

可以看出，第二行是第一行的2倍，第三列是前两列相加，第二列又是第一列4倍，所以秩为1，列空间维度是1.

\(A\) 可以表示成一种更漂亮的形式：

\[\left( \begin{array}{ccc} 1 & 4 & 5 \\ 2 & 8 & 10 \\ \end{array} \right)=\left( \begin{array}{c} 1 \\ 2 \\ \end{array} \right).\left( \begin{array}{ccc} 1 & 4 & 5 \\ \end{array} \right) \]

可以表示成 主列 乘以 主行。

一列乘以一行结果是个矩阵。

所有的秩1矩阵都可以表示为一列乘以一行的形式。

\[A=u.v^T \]

其中，\(u、v\) 表示列向量，\(v\) 转置表示行向量。

秩1矩阵有趣地方在于，她可以称为搭建其他矩阵的“积木”。

如果有一个 \(5*17\) 的矩阵，秩为4,可以把其分解为4个秩1矩阵的组合。

子空间

例1：

所有的秩4矩阵能构成一个子空间吗？

子空间需要满足加法和数乘封闭性。

性质：两个矩阵之和的秩不大于两个矩阵的秩之和。

所以两个秩4矩阵相加，结果可能是秩5矩阵。所以不是子空间。

例2：

假设在 \(R^4\) 空间中，$v=\left(
\begin{array}{c}
v_1 \
v_2 \
v_3 \
v_4 \
\end{array}
\right) $ ,所有的分量满足\(s=v_1+v_2+v_3+v_4=0\) 。\(s\) 是一个子空间吗？是。

证明：

1. 任取某分量之和为零的向量，乘以6的新向量还是在 \(s\) 中；
2. 任取两个满足分量之和为零的向量相加，新向量还是在 \(s\) 中。

\(s\) 的维数和基是什么？

我们可以通过将目标矩阵转换为基本子空间，求四个基本子空间的维度和基的系统方法求出来。

观察 \(s\) 的特点，我们可以联系 \(Ax=0\) 。

即假设 \(s\) 是某个矩阵的零空间，即 \(s=x\),可以找出

\[\left( \begin{array}{cccc} 1 & 1 & 1 & 1 \\ \end{array} \right) \left( \begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ \end{array} \right)=0 \]

因此 \(s=N(A)\),\(A\) 的秩为1，求零空间维数公式为

\[dim[N(A)]=n-r \]

因此 \(s\)在3维空间里面.

自由变量为 \(v_2,v_3,v_4\),依次对她们任意赋值，求出主变量，可以求得三个线性无关向量，这三个线性无关向量就是 \(s\) 的一组基。

\[Basis\quad for\quad s=\left( \begin{array}{c} -1 \\ 1 \\ 0 \\ 0 \\ \end{array} \right),\left( \begin{array}{c} -1 \\ 0 \\ 1 \\ 0 \\ \end{array} \right),\left( \begin{array}{c} -1 \\ 0 \\ 0 \\ 1 \\ \end{array} \right) \]

小世界图

什么是"图"？图是结点和边的集合，边连接结点。

例如，5个点和6条边。

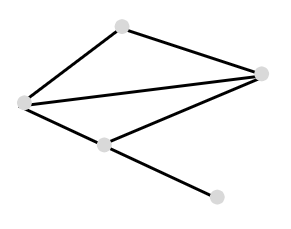
一个\(5*6\) 的矩阵可以表示这个图的全部信息。

有趣的问题是一个结点到任意一个结点共需要多少步？“六度分离猜想”解决了这个问题。下节课分解。