线性代数01.方程组的几何解释
本篇为MIT公开课——线性代数 笔记。
二维举例
两未知数两方程:
方程组的矩阵形式:
这里矩阵有两行两列,左手边包括系数矩阵\(A\),未知数向量 \(X\),右侧 向量\(b\)。
于是线性方程组可以写成 \(A X =b\).
-
行图像
一次取一行方程,作图于 \(xy\) 平面。
做出满足两个方程的所有的点的图像。
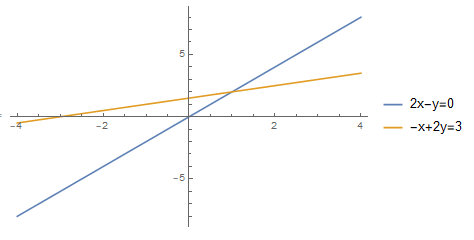
它们相交于点 \((1,2)\)。这个交点也是方程的解。
-
列图像
我们重新看两个方程
两个方程一起考虑,竖着看方程, \(x\) 和 \(y\) 的部分。我们可以写成:
这个方程的目的是寻找如何将左侧的两个已知向量正确组合然后构成右侧的向量。即:\(\left( \begin{array}{c} 2 \\ -1 \\ \end{array} \right)\)和\(\left( \begin{array}{c} -1 \\ 2 \\ \end{array} \right)\)分别乘以对应数值然后相加,来制造向量\(\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right)\),这个过程就是列向量的线性组合。这两个数值就是我们要求解的。
在行图像中我们解出 \(x\) =1, \(y\) =2,带进去列向量组成的方程试试,
这个图像是怎么样的呢?(向量的加法运算)
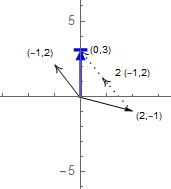
怎么得来的?对于右侧向量,第一个分量就是(从横向看) \(1*2+2*(-1)=0\),第二个分量就是 \(1*(-1)+2*2=3\)
绝了。
那么所有的线性组合又是什么?
结果是我们可以得到所有可能的右侧向量,它们会布满整个坐标平面。也就是会得到一个面。
三维举例
三未知数三方程:
系数矩阵和右侧向量分别为:
-
行图像
三维图像里,每一行方程都是一个平面;在这个例子里面,三个平面互不平行,所以两个平面相交于一条直线,三个平面相交于一个点。
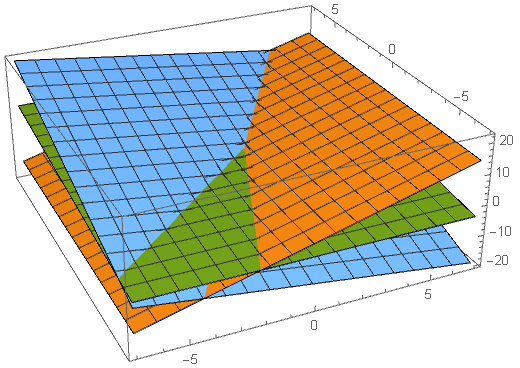
这个点就是我们的解。
但问题显而易见:太难画了!(不用软件) 四维甚至更高维,问题更复杂,更加难画。
此时列图像将展现它的优势。
-
列图像
写出列图像矩阵形式:
左侧,我们要进行三个向量的线性组合,构造出右侧向量。
可以看出,右侧向量是左侧向量其中一个,那么结果很显然:
正确的组合就是0个列1,0个列2,1个列3。
但这一道题是精心设计的,一般我们不会一眼看出结果。但可以看到他比行图像简单得多。
下一讲讲解矩阵消元法,来解方程组。
-
问题
对于该例子,考虑所有的右侧向量,对任意 \(b\) ,是否都能求解 $A*X=b $ ? ,从线性组合角度问,就是“列的线性组合是否能覆盖整个三维空间?”,这两种问法实际上意义是一样的。
该例子中,系数矩阵 \(A\) 是非奇异矩阵和可逆矩阵,所以对于这个矩阵,答案是”可以“。
但对于某些情况,答案可能是否定的,比如三个列向量同处于一个平面,那么它们的组合也一定在这个平面上,问题就出现了,因为 \(b\) 不在这个平面上,所以没有解。这种情况称为奇异,矩阵不可逆。
考虑九维
假设9未知数9方程,这样就有9列,每一列都是9维空间的向量,考虑其线性组合 ,通过正确线性组合得到右侧向量。
-
问题
同样的,是否对于任意$ b$ 都能求解?
这还是取决于这9个向量,有时可以,有时不行。比如9列实际只有8列对结果有贡献,这样就会有一些 \(b\) 无法求得,我们无法得到整个9维空间 。
矩阵乘法
系数矩阵A乘以未知数向量等于右侧向量,这是一种矩阵乘法运算。
如何用矩阵乘以向量?
举例,
两种方法:
1.一次一列形式
取1个第一列和2个第二列
向量的第一个分量乘以矩阵第一列,第二个分量乘以矩阵第二列,然后相加。
2.一次一行形式
矩阵第一行与向量点积得到右侧向量第一个分量,第二行与向量点积得到右侧向量的第二个分量。


